第17章 一元二次方程 复习(3)实际问题与一元二次方程 课件(共28张PPT)
文档属性
| 名称 | 第17章 一元二次方程 复习(3)实际问题与一元二次方程 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 06:07:05 | ||
图片预览






文档简介
(共28张PPT)
沪科版 八年级下册
第17章 一元二次方程 复习(3)
实际问题与一元二次方程
实际问题与一元二次方程
增长(下降)率问题
面积问题
经济效益问题
a(1±x)2=m
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
例.某商场今年9月份的营业额为400万元,10月份的营业额比9月份增加10%,12月份的营业额达到633.6万元,求10月份到12月份营业额的平均月增长率。
解得 x1=0.2=20%,x2=-2.2(舍去)
答:10月份到12月份营业额的平均月增长率为20%.
400(1+10%)(1+x)2=633.6
解:设每月的平均增长率为x,则可列方程为
(一)增长(下降)率问题例析
1.向阳村2016年的人均收入为24000元,2018年的人均收入为29040元,求人均收入的年平均增长率.
解:设所求人均收入的年平均增长率为x.则有:
24000·(1+x)2=29040
解得: x1=0.1=10%,
答:人均收入的年平均增长率为10%.
(二)增长(下降)率问题练习
(1+x)2=1.21
1+x= 1.1
±
(不合题意,舍去)
x2=-2.1
2.某城市在创建“国家森林城市”的过程中,从2019年开始扩大植草、栽树工程,经过两年的努力,使原来城区绿地总面积60公顷,到2021年总面积达到了79.2公顷,这两年的增长率不断提高,后一年的增长率与前一年的增长率相差10%,则前一年的增长率是多少?
解得 x1=0.1=10%,x2=-2.2(舍去).
答:前一年的增长率为10%.
解:设前一年的增长率为x,
可列方程为
60 (1+x) (1+x+10%) =79.2
则后一年的增长率为(x+10%),
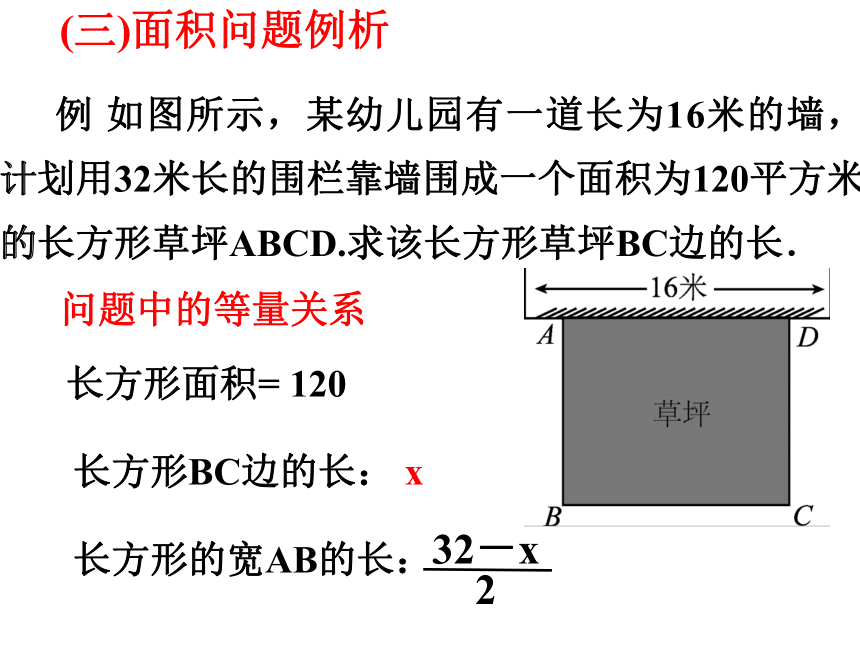
例 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的长方形草坪ABCD.求该长方形草坪BC边的长.
(三)面积问题例析
长方形面积= 120
长方形BC边的长:
问题中的等量关系
长方形的宽AB的长:
x
32-x
2
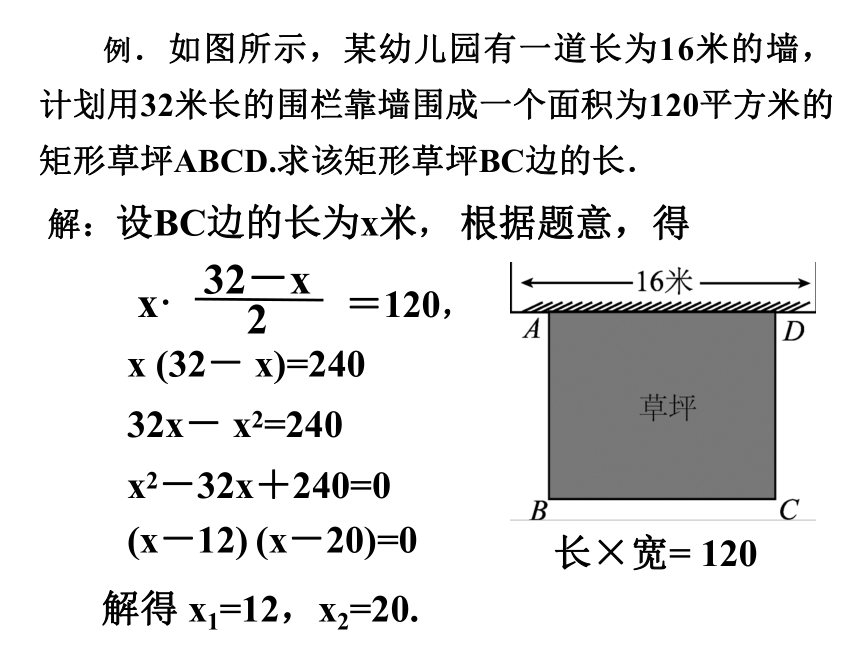
例.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设BC边的长为x米,
x· =120,
32-x
2
长×宽= 120
x (32- x)=240
32x- x2=240
x2-32x+240=0
(x-12)
(x-20)=0
解得 x1=12,x2=20.
根据题意,得
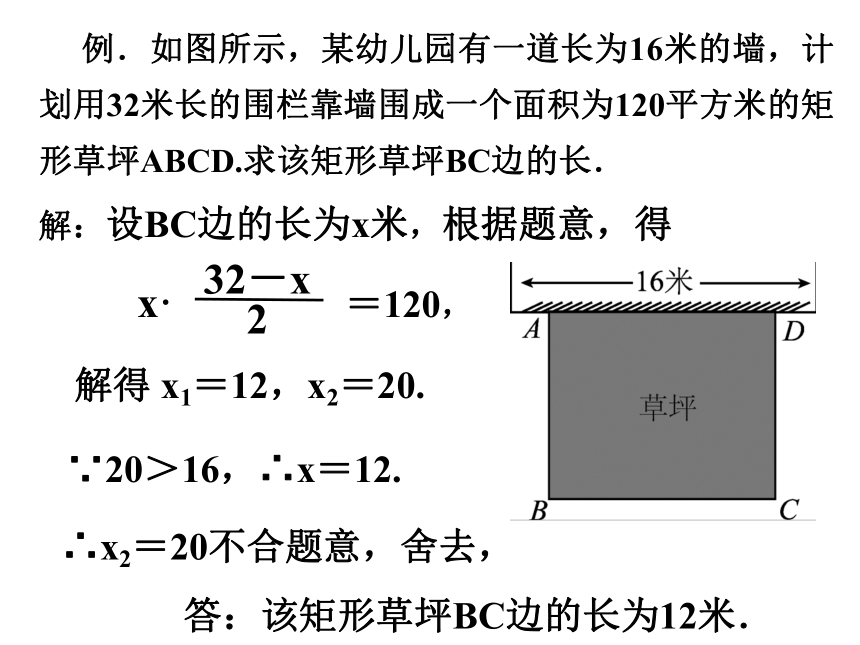
例.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设BC边的长为x米,根据题意,得
x· =120,
解得 x1=12,x2=20.
∵20>16,∴x=12.
答:该矩形草坪BC边的长为12米.
∴x2=20不合题意,舍去,
32-x
2
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
(四)经济效益问题例析
问题中的等量关系
每天销售盈利= 5000元
每台冰箱的利润
×每天冰箱的销量=5000
每件冰箱应定价多少
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
问题中的等量关系
每天销售盈利= 5000元
每台冰箱的盈利
×每天冰箱的销量=5000
每台冰箱应定价x元
(x-2500)
(8+ )
·4
2900- x
50
=5000
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
解:设每台冰箱应定价x元,
根据题意,得
x2-5500x+7562500=0
每台冰箱的盈利
×每天冰箱的销量=5000
(x-2500)
(8+ )
·4
2900- x
50
=5000
∴x1=x2=
(x-2500)
6000-2x
25
·
=5000
(x-2500)
(3000-x)
=2500
·25
∵Δ=0
-(-5500)
2
=2750.
答:每台冰箱应定价2750元.
解:设每台冰箱应定价x元,
解得 x1=x2=2750.
根据题意,得
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
(x-2500)
(8+ )
·4
2900- x
50
=5000
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
问题中的等量关系
顺水航行的时间+逆水航行的时间= 6h
顺水航行的路程
逆水航行的路程
顺水航行的速度
逆水航行的速度
顺水航行的速度=
静水速度
+水流速度
逆水航行的速度=
静水速度
-水流速度
24km
24km
3km/h
xkm/h
+
=6h
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
顺水航行的时间+逆水航行的时间= 6h
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
4
x+3
4
x-3
+
=1
4
(x-3)
4
(x+3)
+
=(x+3)
(x-3)
4x-12
4x+12
+
=x2-9
x2-8x-9=0
(x+1)
(x-9)
=0
x1=9,x2=-1(舍去,不合题意)
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
x1=9,x2=-1(不合题意,舍去)
解这个方程得
当x=9时,
(x+3)
(x-3) ≠ 0,
9是原方程的解.
答:
小艇在静水中的速度为9km/h,
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
问题中的等量关系
第一个月的利润+第二个月的利润= 350
利润= 售价-进价
每盒利润·销售盒数
每盒利润·销售盒数
20%x·
50
-5
( 总盒数-50)
总价
进价
2400
x
每盒茶叶的进价x元
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
问题中的等量关系
第一个月的利润+第二个月的利润=350
20%x·
50
( -50)
2400
x
-5·
=350
每盒茶叶的进价x元
解:设每盒茶叶的进价价为x元,
根据题意,得
20%x·50
+(-5 )
·
( -50)
2400
x
=350
第一个月的利润+第二个月的利润=350
2x
-
( -50)
2400
x
=70
x
-
+25
1200
x
=35
x2-10x-1200=0
(x+30)
(x-40)
=0
x1=40,x2=-30(舍去,不合题意)
答:每盒茶叶的进价为40元.
解:设每盒茶叶的进价为x元,
根据题意,得
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
20%x·50
+(-5 )
( -50)
2400
x
=350
x1=40,x2=-30(舍去,不合题意)
解得
3.一商店用1800元买进玩具若干个,其中有2个损坏无法出售,剩余的每个以比进价多5元的价格出售,若剩余的全部卖完,则这批玩具共赚400元,问这批玩具每个的进价是多少元?共买进了多少个玩具?
问题中的等量关系
卖出玩具的利润-损坏2个的成本=400
-2x
( -2)
1800
x
5·
=400
每个玩具的进价x元
每个玩具的利润·售出的玩具数
6.一商店用1800元买进玩具若干个,其中有2个损坏无法出售,剩余的每个以比进价多5元的价格出售,若剩余的全部卖完,则这批玩具共赚400元,问这批玩具每个的进价是多少元?
答:每个玩具的进价为20元.
解:设每个玩具的进价为x元,
根据题意,得
5 ·
( -2)
=400
x1=20,x2=-225(舍去,不合题意)
解得
-2x
1800
x
今天作业
课本P50页第9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级下册
第17章 一元二次方程 复习(3)
实际问题与一元二次方程
实际问题与一元二次方程
增长(下降)率问题
面积问题
经济效益问题
a(1±x)2=m
列方程解应用题的一般步骤是什么?
第一步:审题,明确已知和未知;
第二步:找相等关系;
第三步:设元,列方程,并解方程;
第五步:作答.
第四步:检验根的合理性;
例.某商场今年9月份的营业额为400万元,10月份的营业额比9月份增加10%,12月份的营业额达到633.6万元,求10月份到12月份营业额的平均月增长率。
解得 x1=0.2=20%,x2=-2.2(舍去)
答:10月份到12月份营业额的平均月增长率为20%.
400(1+10%)(1+x)2=633.6
解:设每月的平均增长率为x,则可列方程为
(一)增长(下降)率问题例析
1.向阳村2016年的人均收入为24000元,2018年的人均收入为29040元,求人均收入的年平均增长率.
解:设所求人均收入的年平均增长率为x.则有:
24000·(1+x)2=29040
解得: x1=0.1=10%,
答:人均收入的年平均增长率为10%.
(二)增长(下降)率问题练习
(1+x)2=1.21
1+x= 1.1
±
(不合题意,舍去)
x2=-2.1
2.某城市在创建“国家森林城市”的过程中,从2019年开始扩大植草、栽树工程,经过两年的努力,使原来城区绿地总面积60公顷,到2021年总面积达到了79.2公顷,这两年的增长率不断提高,后一年的增长率与前一年的增长率相差10%,则前一年的增长率是多少?
解得 x1=0.1=10%,x2=-2.2(舍去).
答:前一年的增长率为10%.
解:设前一年的增长率为x,
可列方程为
60 (1+x) (1+x+10%) =79.2
则后一年的增长率为(x+10%),
例 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的长方形草坪ABCD.求该长方形草坪BC边的长.
(三)面积问题例析
长方形面积= 120
长方形BC边的长:
问题中的等量关系
长方形的宽AB的长:
x
32-x
2
例.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设BC边的长为x米,
x· =120,
32-x
2
长×宽= 120
x (32- x)=240
32x- x2=240
x2-32x+240=0
(x-12)
(x-20)=0
解得 x1=12,x2=20.
根据题意,得
例.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
解:设BC边的长为x米,根据题意,得
x· =120,
解得 x1=12,x2=20.
∵20>16,∴x=12.
答:该矩形草坪BC边的长为12米.
∴x2=20不合题意,舍去,
32-x
2
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
(四)经济效益问题例析
问题中的等量关系
每天销售盈利= 5000元
每台冰箱的利润
×每天冰箱的销量=5000
每件冰箱应定价多少
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
问题中的等量关系
每天销售盈利= 5000元
每台冰箱的盈利
×每天冰箱的销量=5000
每台冰箱应定价x元
(x-2500)
(8+ )
·4
2900- x
50
=5000
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
解:设每台冰箱应定价x元,
根据题意,得
x2-5500x+7562500=0
每台冰箱的盈利
×每天冰箱的销量=5000
(x-2500)
(8+ )
·4
2900- x
50
=5000
∴x1=x2=
(x-2500)
6000-2x
25
·
=5000
(x-2500)
(3000-x)
=2500
·25
∵Δ=0
-(-5500)
2
=2750.
答:每台冰箱应定价2750元.
解:设每台冰箱应定价x元,
解得 x1=x2=2750.
根据题意,得
例. 新华商场销售某种冰箱,每台进货价为2500元,市场调研表明:当销售价为2900元/台时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
(x-2500)
(8+ )
·4
2900- x
50
=5000
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
问题中的等量关系
顺水航行的时间+逆水航行的时间= 6h
顺水航行的路程
逆水航行的路程
顺水航行的速度
逆水航行的速度
顺水航行的速度=
静水速度
+水流速度
逆水航行的速度=
静水速度
-水流速度
24km
24km
3km/h
xkm/h
+
=6h
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
顺水航行的时间+逆水航行的时间= 6h
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
4
x+3
4
x-3
+
=1
4
(x-3)
4
(x+3)
+
=(x+3)
(x-3)
4x-12
4x+12
+
=x2-9
x2-8x-9=0
(x+1)
(x-9)
=0
x1=9,x2=-1(舍去,不合题意)
1.一小艇顺流航行24km到达目的地,然后逆流回到出发地,航行时间共6h.已知水流速度是3km/h.求小艇在静水中的速度.
小艇在静水中的速度为xkm/h,
解:
根据题意,得
24
x+3
24
x-3
+
=6
x1=9,x2=-1(不合题意,舍去)
解这个方程得
当x=9时,
(x+3)
(x-3) ≠ 0,
9是原方程的解.
答:
小艇在静水中的速度为9km/h,
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
问题中的等量关系
第一个月的利润+第二个月的利润= 350
利润= 售价-进价
每盒利润·销售盒数
每盒利润·销售盒数
20%x·
50
-5
( 总盒数-50)
总价
进价
2400
x
每盒茶叶的进价x元
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
问题中的等量关系
第一个月的利润+第二个月的利润=350
20%x·
50
( -50)
2400
x
-5·
=350
每盒茶叶的进价x元
解:设每盒茶叶的进价价为x元,
根据题意,得
20%x·50
+(-5 )
·
( -50)
2400
x
=350
第一个月的利润+第二个月的利润=350
2x
-
( -50)
2400
x
=70
x
-
+25
1200
x
=35
x2-10x-1200=0
(x+30)
(x-40)
=0
x1=40,x2=-30(舍去,不合题意)
答:每盒茶叶的进价为40元.
解:设每盒茶叶的进价为x元,
根据题意,得
2.某商店以2400元购进一种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒.第二个月以低于进价5元作为售价,售完余下的茶叶.全部售完后共盈利350元,求每盒茶叶的进价.
20%x·50
+(-5 )
( -50)
2400
x
=350
x1=40,x2=-30(舍去,不合题意)
解得
3.一商店用1800元买进玩具若干个,其中有2个损坏无法出售,剩余的每个以比进价多5元的价格出售,若剩余的全部卖完,则这批玩具共赚400元,问这批玩具每个的进价是多少元?共买进了多少个玩具?
问题中的等量关系
卖出玩具的利润-损坏2个的成本=400
-2x
( -2)
1800
x
5·
=400
每个玩具的进价x元
每个玩具的利润·售出的玩具数
6.一商店用1800元买进玩具若干个,其中有2个损坏无法出售,剩余的每个以比进价多5元的价格出售,若剩余的全部卖完,则这批玩具共赚400元,问这批玩具每个的进价是多少元?
答:每个玩具的进价为20元.
解:设每个玩具的进价为x元,
根据题意,得
5 ·
( -2)
=400
x1=20,x2=-225(舍去,不合题意)
解得
-2x
1800
x
今天作业
课本P50页第9、10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
