第20章数据的初步分析 复习课件(共33张PPT)
文档属性
| 名称 | 第20章数据的初步分析 复习课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第20章 数据的初步分析
复习课件
沪科版 八年级下册
(1)本章我们学习了哪些统计的量?
这些统计的量各有什么特点?
怎样用它们做数据分析?
(2)在数据分析时,怎样运用样本估计
总体的方法的?
(3)统计一般分哪些步骤进行?
1.频数与频率:
在n个数据中,某类数据出现的次数m称为该类数据出现的频数, 称为该类数据出现的频率.
主要知识回顾
m
n
用频数分布直方图描述数据的一般步骤是:
(1)
(2)
(3)
(4)
(5)
计算最大值最小值的差
决定组距和组数
决定分点
列频数分布表
绘制频数直方图
算术平均数:
2.平均数
X
=
1
n
(x1+x2+ … +xn)
加权平均数:
X
=
x1f1+x2f2+ … +xkfk
f1+f2+ … +fk
样本平均数
总体平均数
平均数计算要用到所有的数据,任何一个数据的变动都会相应引起平均数的变动,它能够充分利用所有的数据信息,但它受极端值的影响较大.
3.请说说平均数、众数和中位数这三个统计量的各自特点.
请说说平均数、众数和中位数这三个统计量的各自特点.
中位数仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给的数据中.当一组数据中的个别数据变动较大时,可用中位数描述其趋势,中位数的计算很少.
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,缺点是当众数有多个且众数的频数相对较小时可靠性小,局限性大.
请说说平均数、众数和中位数这三个统计量的各自特点.
方差的计算步骤:
S2=
1
n
1.计算样本数据的平均数,
2.计算各个数据与平均数的差的平方,
3.计算各个数据与平均数的差的平方
的平均数.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
4.方差的计算公式:
5.用样本数据估计总体数据
(1)样本平均数估计总体平均数:
现实生活中总体平均数一般难以计算出来,常采用样本平均数估计总体平均数,若样本容量太小,则差异较大
(2)用样本方差估计总体方差:
在实际问题中也常采用样本方差估计总体方差
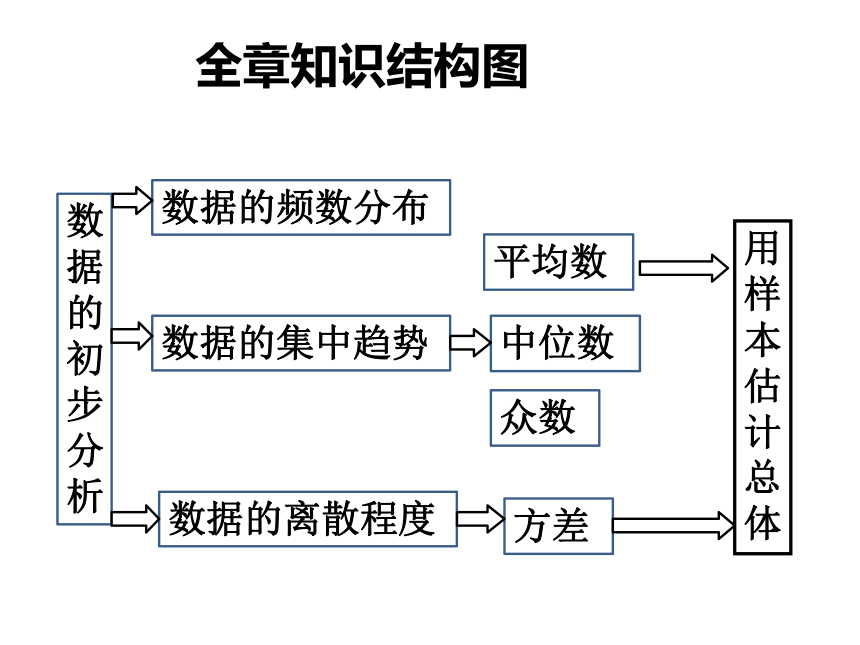
全章知识结构图
数据的初步分析
数据的频数分布
数据的集中趋势
数据的离散程度
平均数
众数
中位数
方差
用
样
本
估
计
总
体
例1 为了解我校八年级300名学生的视力情况,从中抽取了一部分学生的视力情况,进行数据整理后:
(1)在这个问题中,总体,个体分别是什么?
总体:我校八年级300名学生的视力情况;
个体:我校八年级每一名学生的视力情况.
(一)数据的初步分析典型例析:
(2)填写频数统计表中未完成的部分:
分组 频数 频率
3.95~4.25 2 0.04
6 0.12
4.55~4.85 23
4.85~5.15
5.15~5.45 1 0.02
合计 1.00
4.25~4.55
50
0.46
18
0.36
(3)若视力为4.9,5.0,5.1均属正常,不需
矫正,试估计我校八年级学生视力正常的
人数约为多少?
50人中视力为4.9,5.0,5.1的人数为18人,
占50人的百分比为18÷50=36%,
∴我校八年级学生视力正常的人数约为:
300×36%=108(名)
频数
视力
3.95 4.25 4.55 4.85 5.15 5.45
0
5
10
15
20
25
(4)画出频数分布直方图.
例2.我校九年级125班20名女生某次体育
测试成绩统计如下表:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生的体育测试成绩的平均分是82分,求x、y的值;
解:(1)由题意,得
解得
∴ x的值为5,y的值为7.
1+5+x+y+2 =20
x=5
y=7
(60×1+70×5+80x+90y+100×2)=82
1
20
x+y=12
8x+9y=103
(2)在(1)的条件下,设20名女生本次
体育测试成绩的众数是a,中位数是b,
求(a-b)2的值.
(2)由题意,得
众数a=90,中位数b=80,
∴(a-b)2=(90-80)2=100,
∴(a-b)2的值为100.
例3.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
甲 95 82 88 81 93 79 84 78
乙 83 92 80 95 90 80 85 75
解:分别求出甲、乙两人的平均数和方差,得
(82+81+…+84)=85,
[(78-85)2+(79-85)2+…+(95-85)2]
∴
S2甲
=
∵
X甲
=
1
8
=35.5
1
8
(92+95+…+85)=85,
X乙
=
1
8
[(92-85)2+(95-85)2+…+(85-85)2]
S2乙
=
=41
1
8
∵
X甲
=
X乙
,
S2甲
S2乙
,
∴甲的成绩较稳定,派甲参赛比较合适.
<
4.我市一花农对10盆同一品种的花施用甲、乙两种花肥,把10盆花分成甲、乙两组,每组5盆,记录其花期(单位:天)如下:
甲组:25,23,28,22,27;
乙组:27,24,24,27,23.
(1)10盆花的花期最多相差几天?
(2)施用何种花肥,花的平均花期较长?
(3)施用哪种花肥的效果更好?
解:
(25+23+…+25)=25,
∵
X甲
=
1
5
(27+24+…+23)=25,
X乙
=
1
5
∴
X甲
=
X乙
,
∴不论施用哪种花肥,花的平均花期一样长.
(1) 28-22=6(天).
(2)
[(25-25)2+(23-25)2+…+(95-85)2]
∴
S2甲
=
=5.2
1
5
[(92-85)2+(95-85)2+…+(85-85)2]
S2乙
=
=2.8
1
5
∵
X甲
=
X乙
,
S2甲
S2乙
,
∴施用乙种花肥效果比较可靠.
>
1.我市公务员招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数作为总成绩,王强笔试90分,面试85分,则
他的总成绩为___分.
88
(2)能力小测试
2.若5个正整数的中位数是3,唯一的众数是7,则这5个数的平均数是___.
4
能力小测试
能力小测试
3.一组数据按从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为( )
A.4 B.8 C.10 D.14
C
能力小测试
5.已知一组数据5,8,10,x,9的众数是8,则这组数据的方差是( )
A. 2.6 B. 2.7 C. 2.8 D. 2.9
C
4.数据-2,-1,0,3,5的方差是____.
6.8
6.为了从甲、乙两名同学中选拔一人参加我市中学生数学竞赛,每个月学校对他们的学习进行一次测试,如图是两人赛前5次测试成绩的折线统计图.
(1)分别求出甲、乙两人的平均数和方差 ;
_____, _____,
=_____, =____.
80
80
70
50
X甲
=
X乙
=
S2甲
S2乙
(2)若你是他们的辅导老师,应该选派谁去参赛?为什么?
乙的成虽然较稳定,但最近两次成绩都低于甲,且甲最近三次成绩稳中有升,而乙却有下降趋势,所以应派甲去参赛.
今天作业
课本P142页第1题
课本P145页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第20章 数据的初步分析
复习课件
沪科版 八年级下册
(1)本章我们学习了哪些统计的量?
这些统计的量各有什么特点?
怎样用它们做数据分析?
(2)在数据分析时,怎样运用样本估计
总体的方法的?
(3)统计一般分哪些步骤进行?
1.频数与频率:
在n个数据中,某类数据出现的次数m称为该类数据出现的频数, 称为该类数据出现的频率.
主要知识回顾
m
n
用频数分布直方图描述数据的一般步骤是:
(1)
(2)
(3)
(4)
(5)
计算最大值最小值的差
决定组距和组数
决定分点
列频数分布表
绘制频数直方图
算术平均数:
2.平均数
X
=
1
n
(x1+x2+ … +xn)
加权平均数:
X
=
x1f1+x2f2+ … +xkfk
f1+f2+ … +fk
样本平均数
总体平均数
平均数计算要用到所有的数据,任何一个数据的变动都会相应引起平均数的变动,它能够充分利用所有的数据信息,但它受极端值的影响较大.
3.请说说平均数、众数和中位数这三个统计量的各自特点.
请说说平均数、众数和中位数这三个统计量的各自特点.
中位数仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给的数据中.当一组数据中的个别数据变动较大时,可用中位数描述其趋势,中位数的计算很少.
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,缺点是当众数有多个且众数的频数相对较小时可靠性小,局限性大.
请说说平均数、众数和中位数这三个统计量的各自特点.
方差的计算步骤:
S2=
1
n
1.计算样本数据的平均数,
2.计算各个数据与平均数的差的平方,
3.计算各个数据与平均数的差的平方
的平均数.
[(x1-x)2+(x2-x)2+…+(xn-x)2]
4.方差的计算公式:
5.用样本数据估计总体数据
(1)样本平均数估计总体平均数:
现实生活中总体平均数一般难以计算出来,常采用样本平均数估计总体平均数,若样本容量太小,则差异较大
(2)用样本方差估计总体方差:
在实际问题中也常采用样本方差估计总体方差
全章知识结构图
数据的初步分析
数据的频数分布
数据的集中趋势
数据的离散程度
平均数
众数
中位数
方差
用
样
本
估
计
总
体
例1 为了解我校八年级300名学生的视力情况,从中抽取了一部分学生的视力情况,进行数据整理后:
(1)在这个问题中,总体,个体分别是什么?
总体:我校八年级300名学生的视力情况;
个体:我校八年级每一名学生的视力情况.
(一)数据的初步分析典型例析:
(2)填写频数统计表中未完成的部分:
分组 频数 频率
3.95~4.25 2 0.04
6 0.12
4.55~4.85 23
4.85~5.15
5.15~5.45 1 0.02
合计 1.00
4.25~4.55
50
0.46
18
0.36
(3)若视力为4.9,5.0,5.1均属正常,不需
矫正,试估计我校八年级学生视力正常的
人数约为多少?
50人中视力为4.9,5.0,5.1的人数为18人,
占50人的百分比为18÷50=36%,
∴我校八年级学生视力正常的人数约为:
300×36%=108(名)
频数
视力
3.95 4.25 4.55 4.85 5.15 5.45
0
5
10
15
20
25
(4)画出频数分布直方图.
例2.我校九年级125班20名女生某次体育
测试成绩统计如下表:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生的体育测试成绩的平均分是82分,求x、y的值;
解:(1)由题意,得
解得
∴ x的值为5,y的值为7.
1+5+x+y+2 =20
x=5
y=7
(60×1+70×5+80x+90y+100×2)=82
1
20
x+y=12
8x+9y=103
(2)在(1)的条件下,设20名女生本次
体育测试成绩的众数是a,中位数是b,
求(a-b)2的值.
(2)由题意,得
众数a=90,中位数b=80,
∴(a-b)2=(90-80)2=100,
∴(a-b)2的值为100.
例3.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
甲 95 82 88 81 93 79 84 78
乙 83 92 80 95 90 80 85 75
解:分别求出甲、乙两人的平均数和方差,得
(82+81+…+84)=85,
[(78-85)2+(79-85)2+…+(95-85)2]
∴
S2甲
=
∵
X甲
=
1
8
=35.5
1
8
(92+95+…+85)=85,
X乙
=
1
8
[(92-85)2+(95-85)2+…+(85-85)2]
S2乙
=
=41
1
8
∵
X甲
=
X乙
,
S2甲
S2乙
,
∴甲的成绩较稳定,派甲参赛比较合适.
<
4.我市一花农对10盆同一品种的花施用甲、乙两种花肥,把10盆花分成甲、乙两组,每组5盆,记录其花期(单位:天)如下:
甲组:25,23,28,22,27;
乙组:27,24,24,27,23.
(1)10盆花的花期最多相差几天?
(2)施用何种花肥,花的平均花期较长?
(3)施用哪种花肥的效果更好?
解:
(25+23+…+25)=25,
∵
X甲
=
1
5
(27+24+…+23)=25,
X乙
=
1
5
∴
X甲
=
X乙
,
∴不论施用哪种花肥,花的平均花期一样长.
(1) 28-22=6(天).
(2)
[(25-25)2+(23-25)2+…+(95-85)2]
∴
S2甲
=
=5.2
1
5
[(92-85)2+(95-85)2+…+(85-85)2]
S2乙
=
=2.8
1
5
∵
X甲
=
X乙
,
S2甲
S2乙
,
∴施用乙种花肥效果比较可靠.
>
1.我市公务员招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数作为总成绩,王强笔试90分,面试85分,则
他的总成绩为___分.
88
(2)能力小测试
2.若5个正整数的中位数是3,唯一的众数是7,则这5个数的平均数是___.
4
能力小测试
能力小测试
3.一组数据按从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为( )
A.4 B.8 C.10 D.14
C
能力小测试
5.已知一组数据5,8,10,x,9的众数是8,则这组数据的方差是( )
A. 2.6 B. 2.7 C. 2.8 D. 2.9
C
4.数据-2,-1,0,3,5的方差是____.
6.8
6.为了从甲、乙两名同学中选拔一人参加我市中学生数学竞赛,每个月学校对他们的学习进行一次测试,如图是两人赛前5次测试成绩的折线统计图.
(1)分别求出甲、乙两人的平均数和方差 ;
_____, _____,
=_____, =____.
80
80
70
50
X甲
=
X乙
=
S2甲
S2乙
(2)若你是他们的辅导老师,应该选派谁去参赛?为什么?
乙的成虽然较稳定,但最近两次成绩都低于甲,且甲最近三次成绩稳中有升,而乙却有下降趋势,所以应派甲去参赛.
今天作业
课本P142页第1题
课本P145页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
