第19章 四边形 复习(3) 矩形 菱形 正方形 课件(共32张PPT)
文档属性
| 名称 | 第19章 四边形 复习(3) 矩形 菱形 正方形 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 942.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
沪科版 八年级下册
矩形 菱形 正方形
第19章四边形 复习(3)
(2)矩形的___个角都是直角.
(3)矩形的对角线 .
(1)矩形的对边 .
1.矩形的定义:
有一个角是_____的___________叫做矩形.
矩形
直角
平行四边形
平行且相等
四
互相平分且相等
2.矩形的性质:
3.矩形的判定:
(1)有一个角是_____的___________是矩形.
(2)有___个角是直角的四边形是矩形.
(3)对角线_____的平行四边形是矩形.
矩形
直角
平行四边形
三
相等
1.菱形的定义:
一组_____相等的___________叫做菱形.
2.菱形的性质:
(1)菱形的____条边都相等;
(2) 菱形的对边平行;
(3)菱形的对角线 ,并且每条对角线平分__________ .
菱形
邻边
平行四边形
互相垂直平分
一组对角
四
3.菱形的判定:
(1)有一组_____相等的___________是菱形;
(2) ___条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形.
菱形
邻边
平行四边形
四
互相垂直
1.正方形的定义:
有一组_____相等,并且有一个角是_____的平行四边形叫做正方形.
2.正方形的性质:
(1)正方形的四条边都____ ;
(2)正方形的___个角都是直角,
(3)正方形的对角线_____ ,并且____________,每条对角线平分一组_____ .
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
(3)有一个角是 的菱形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(1)有一组_____相等,并且有一个角是_____的
平行四边形的叫做正方形.
(4)对角线__________的矩形是正方形.
(5)对角线______的菱形是正方形.
(6)对角线 的四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
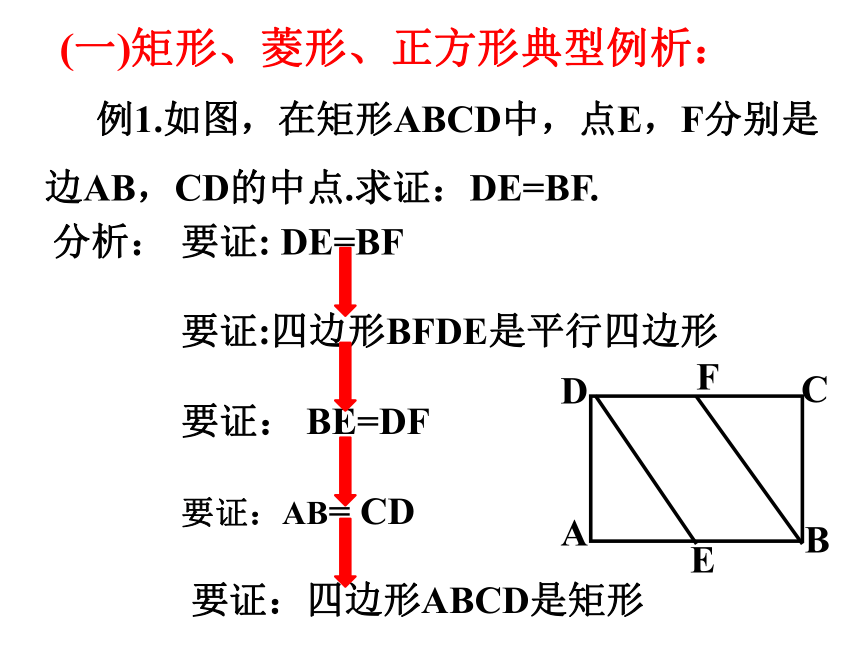
(一)矩形、菱形、正方形典型例析:
例1.如图,在矩形ABCD中,点E,F分别是边AB,CD的中点.求证:DE=BF.
D
A
B
C
E
F
分析:
要证:AB= CD
要证: BE=DF
要证:四边形BFDE是平行四边形
要证: DE=BF
要证:四边形ABCD是矩形
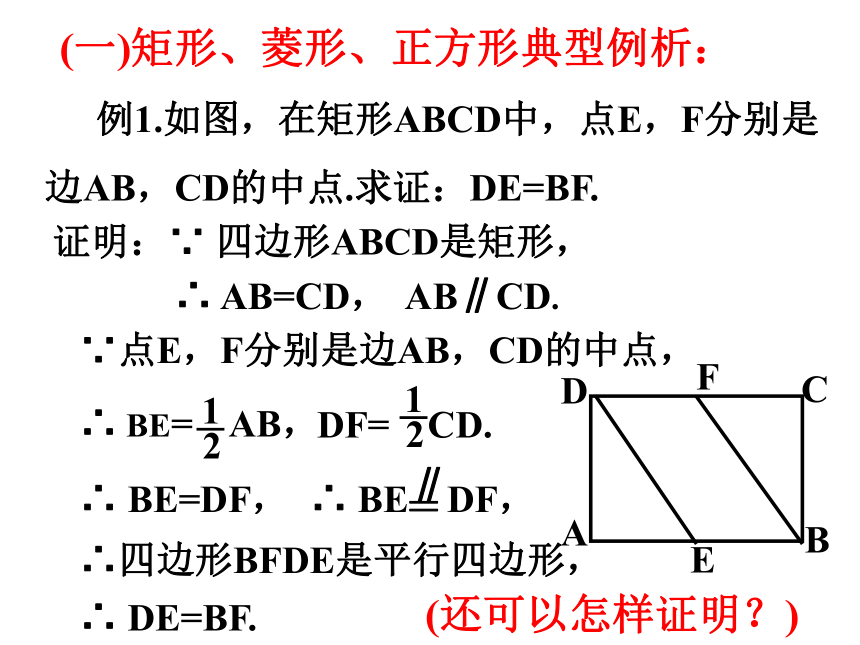
(一)矩形、菱形、正方形典型例析:
例1.如图,在矩形ABCD中,点E,F分别是边AB,CD的中点.求证:DE=BF.
D
A
B
C
E
F
∴ AB=CD,
证明:∵ 四边形ABCD是矩形,
AB∥CD.
∵点E,F分别是边AB,CD的中点,
∴ BE= AB,
DF= CD.
1
2
1
2
∴ BE=DF,
∴ BE DF,
=
∥
∴四边形BFDE是平行四边形,
∴ DE=BF.
(还可以怎样证明?)
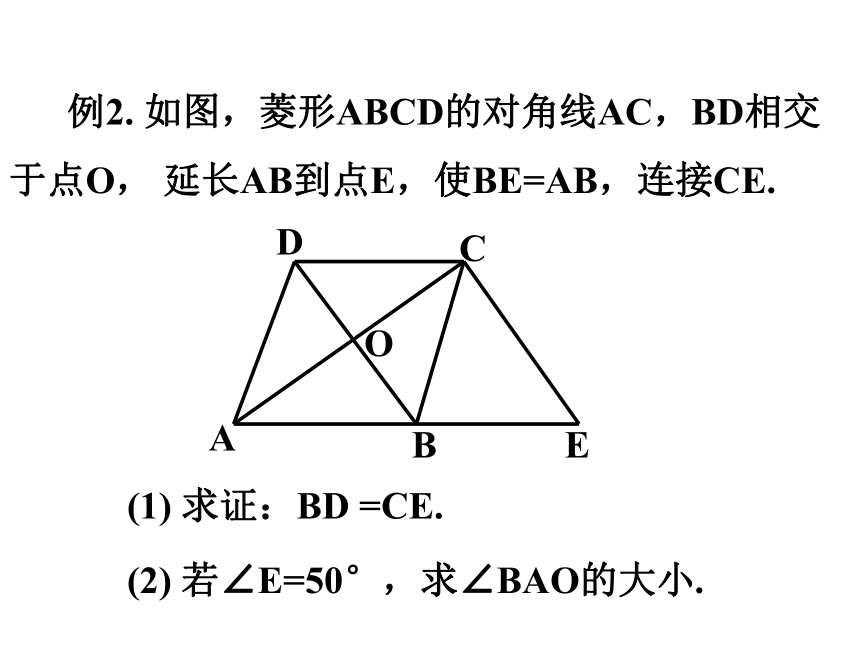
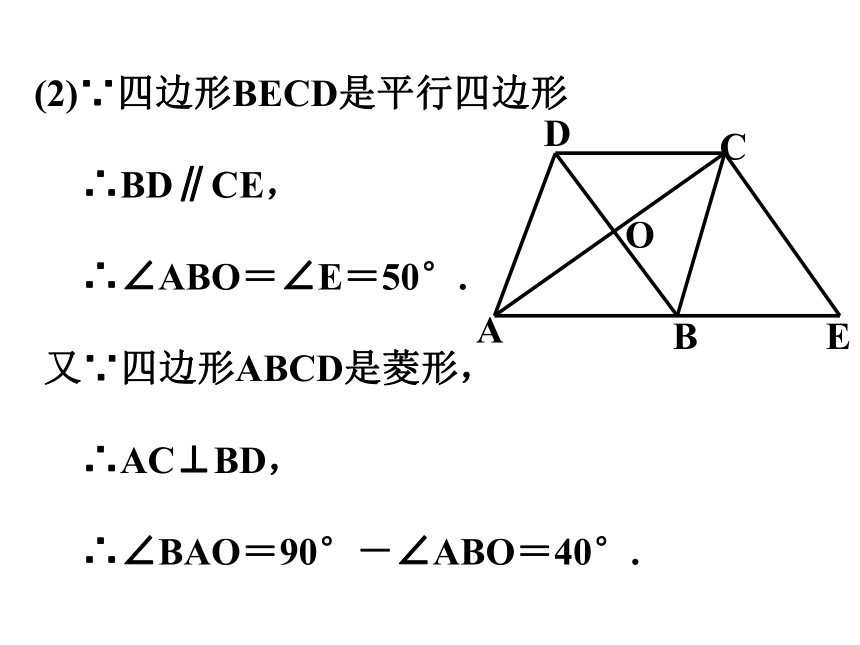
例2. 如图,菱形ABCD的对角线AC,BD相交于点O, 延长AB到点E,使BE=AB,连接CE.
A
B
O
D
E
C
(1) 求证:BD =CE.
(2) 若∠E=50°,求∠BAO的大小.
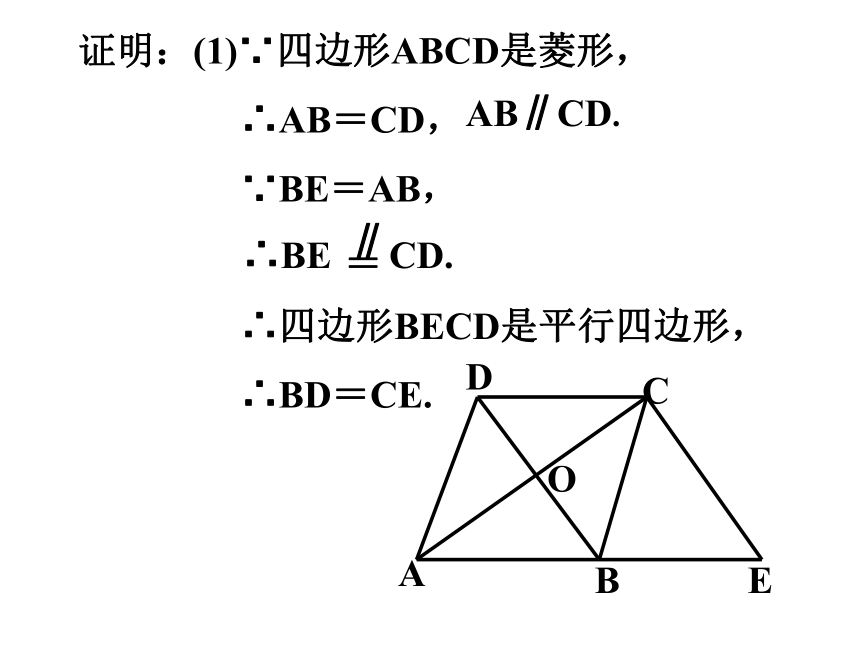
证明:(1)∵四边形ABCD是菱形,
∴AB=CD,
∵BE=AB,
∴四边形BECD是平行四边形,
∴BD=CE.
A
B
O
D
E
C
∴BE CD.
=
∥
AB∥CD.
(2)∵四边形BECD是平行四边形
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
A
B
O
D
E
C
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
(2)连接AC交EF于点O,
延长OC至点M,使OM=OA,
连接EM、FM.判断四边形
AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
A
B
C
D
E
F
O
M
分析:
要证:AB= AD ∠B=∠D
要证:△ABE≌△ADF
要证:∠BAE=∠DAF
要证:四边形ABCD是正方形
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
A
B
C
D
E
F
O
M
∴ AB=BC=CD=AD,
(1)证明:∵ 四边形ABCD是正方形,
∠B=∠D=90°.
∵AE=AF,
∴△ABE≌△ADF(HL).
∴ ∠BAE=∠DAF.
(2) 判断四边形AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
(2)
分析:
要证:CE= CF
要证: OE=OF
要证:四边形AEMF是平行四边形
要证:四边形AEMF是菱形
要证:BE=DF
要证:△ABE≌△ADF
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(2)连接AC交EF于点O,
延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
(2)
四边形AEMF菱形.
理由如下:
∵△ABE≌△ADF(HL).
∴ BE=DF.
∴ BC-BE=CD-DF,
∴ CE=CF.
∴△CEF是等腰三角形.
A
B
C
D
E
F
O
M
(2)
四边形AEMF菱形.
理由如下:
∵△ABE≌△ADF(HL).
∴ BE=DF.
∴ BC-BE=CD-DF,
∴ CE=CF.
∵ 四边形ABCD是正方形,
∴AC平分∠ECF.
∴ OE=OF.
∵OA=OM,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴四边形AEMF是菱形.
∴△CEF是等腰三角形.
1.如图,在矩形ABCD中,对角线AC,BD交于点O,AB=AO=4,则BC= .
A
B
C
D
O
3
4
AO=4,
AC=8,
BC2=AC2-AB2=82-42
=48
(二)矩形、菱形、正方形的练习:
2.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOB=60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
A
B
C
D
O
D
3.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2,AC=2,则BD的长为 .
4.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=3,那么菱形ABCD的周长是( ).
A.6 B.12 C.18 D.24
C
A
B
D
E
F
D
5.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
B
6.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )
( A) 10°
( B) 15°
( C) 20°
A
B
C
D
E
B
7. 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
C
B
O
A
D
O
解:
∵四边形ABCD是平行四边形,
∴ OA= AC,
OD= BD.
1
2
1
2
∵OA=OD,
∴ AC=BD.
∴四边形ABCD是矩形.
∴∠DAB=90°.
∵∠OAD=50°,
∴∠OAB=40°.
8. 如图,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
A
B
C
D
E
F
证明:
∵AD平分∠BAC,
∵DE∥AC,
DF∥AB,
∴四边形AEDF是菱形.
∴ ∠1=∠2.
∵DE∥AC,
∴ ∠1=∠3,
∴ ∠2=∠3,
∴ AE=ED,
∴四边形ABCD是平行四边形.
1
2
3
9. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AC,PN⊥CD,垂足分别为M、N.
(1) 求证:∠ADB=∠CDB.
(2) 若∠ADC=90°,求证四边形MPND是正方形.
A
B
C
D
P
M
N
证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵AB=BC,BD=BD,
∴△ABD≌△CBD.
∴∠ADB=∠CDB.
A
B
C
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN.
∴四边形MPND是正方形.
A
B
C
D
P
M
N
今天作业
课本P104页第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级下册
矩形 菱形 正方形
第19章四边形 复习(3)
(2)矩形的___个角都是直角.
(3)矩形的对角线 .
(1)矩形的对边 .
1.矩形的定义:
有一个角是_____的___________叫做矩形.
矩形
直角
平行四边形
平行且相等
四
互相平分且相等
2.矩形的性质:
3.矩形的判定:
(1)有一个角是_____的___________是矩形.
(2)有___个角是直角的四边形是矩形.
(3)对角线_____的平行四边形是矩形.
矩形
直角
平行四边形
三
相等
1.菱形的定义:
一组_____相等的___________叫做菱形.
2.菱形的性质:
(1)菱形的____条边都相等;
(2) 菱形的对边平行;
(3)菱形的对角线 ,并且每条对角线平分__________ .
菱形
邻边
平行四边形
互相垂直平分
一组对角
四
3.菱形的判定:
(1)有一组_____相等的___________是菱形;
(2) ___条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形.
菱形
邻边
平行四边形
四
互相垂直
1.正方形的定义:
有一组_____相等,并且有一个角是_____的平行四边形叫做正方形.
2.正方形的性质:
(1)正方形的四条边都____ ;
(2)正方形的___个角都是直角,
(3)正方形的对角线_____ ,并且____________,每条对角线平分一组_____ .
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
(3)有一个角是 的菱形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(1)有一组_____相等,并且有一个角是_____的
平行四边形的叫做正方形.
(4)对角线__________的矩形是正方形.
(5)对角线______的菱形是正方形.
(6)对角线 的四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
(一)矩形、菱形、正方形典型例析:
例1.如图,在矩形ABCD中,点E,F分别是边AB,CD的中点.求证:DE=BF.
D
A
B
C
E
F
分析:
要证:AB= CD
要证: BE=DF
要证:四边形BFDE是平行四边形
要证: DE=BF
要证:四边形ABCD是矩形
(一)矩形、菱形、正方形典型例析:
例1.如图,在矩形ABCD中,点E,F分别是边AB,CD的中点.求证:DE=BF.
D
A
B
C
E
F
∴ AB=CD,
证明:∵ 四边形ABCD是矩形,
AB∥CD.
∵点E,F分别是边AB,CD的中点,
∴ BE= AB,
DF= CD.
1
2
1
2
∴ BE=DF,
∴ BE DF,
=
∥
∴四边形BFDE是平行四边形,
∴ DE=BF.
(还可以怎样证明?)
例2. 如图,菱形ABCD的对角线AC,BD相交于点O, 延长AB到点E,使BE=AB,连接CE.
A
B
O
D
E
C
(1) 求证:BD =CE.
(2) 若∠E=50°,求∠BAO的大小.
证明:(1)∵四边形ABCD是菱形,
∴AB=CD,
∵BE=AB,
∴四边形BECD是平行四边形,
∴BD=CE.
A
B
O
D
E
C
∴BE CD.
=
∥
AB∥CD.
(2)∵四边形BECD是平行四边形
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
A
B
O
D
E
C
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
(2)连接AC交EF于点O,
延长OC至点M,使OM=OA,
连接EM、FM.判断四边形
AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
A
B
C
D
E
F
O
M
分析:
要证:AB= AD ∠B=∠D
要证:△ABE≌△ADF
要证:∠BAE=∠DAF
要证:四边形ABCD是正方形
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:∠BAE=∠DAF;
A
B
C
D
E
F
O
M
∴ AB=BC=CD=AD,
(1)证明:∵ 四边形ABCD是正方形,
∠B=∠D=90°.
∵AE=AF,
∴△ABE≌△ADF(HL).
∴ ∠BAE=∠DAF.
(2) 判断四边形AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
(2)
分析:
要证:CE= CF
要证: OE=OF
要证:四边形AEMF是平行四边形
要证:四边形AEMF是菱形
要证:BE=DF
要证:△ABE≌△ADF
例3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.(2)连接AC交EF于点O,
延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明理由.
A
B
C
D
E
F
O
M
(2)
四边形AEMF菱形.
理由如下:
∵△ABE≌△ADF(HL).
∴ BE=DF.
∴ BC-BE=CD-DF,
∴ CE=CF.
∴△CEF是等腰三角形.
A
B
C
D
E
F
O
M
(2)
四边形AEMF菱形.
理由如下:
∵△ABE≌△ADF(HL).
∴ BE=DF.
∴ BC-BE=CD-DF,
∴ CE=CF.
∵ 四边形ABCD是正方形,
∴AC平分∠ECF.
∴ OE=OF.
∵OA=OM,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴四边形AEMF是菱形.
∴△CEF是等腰三角形.
1.如图,在矩形ABCD中,对角线AC,BD交于点O,AB=AO=4,则BC= .
A
B
C
D
O
3
4
AO=4,
AC=8,
BC2=AC2-AB2=82-42
=48
(二)矩形、菱形、正方形的练习:
2.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOB=60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
A
B
C
D
O
D
3.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2,AC=2,则BD的长为 .
4.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=3,那么菱形ABCD的周长是( ).
A.6 B.12 C.18 D.24
C
A
B
D
E
F
D
5.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
B
6.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )
( A) 10°
( B) 15°
( C) 20°
A
B
C
D
E
B
7. 如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
C
B
O
A
D
O
解:
∵四边形ABCD是平行四边形,
∴ OA= AC,
OD= BD.
1
2
1
2
∵OA=OD,
∴ AC=BD.
∴四边形ABCD是矩形.
∴∠DAB=90°.
∵∠OAD=50°,
∴∠OAB=40°.
8. 如图,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
A
B
C
D
E
F
证明:
∵AD平分∠BAC,
∵DE∥AC,
DF∥AB,
∴四边形AEDF是菱形.
∴ ∠1=∠2.
∵DE∥AC,
∴ ∠1=∠3,
∴ ∠2=∠3,
∴ AE=ED,
∴四边形ABCD是平行四边形.
1
2
3
9. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AC,PN⊥CD,垂足分别为M、N.
(1) 求证:∠ADB=∠CDB.
(2) 若∠ADC=90°,求证四边形MPND是正方形.
A
B
C
D
P
M
N
证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵AB=BC,BD=BD,
∴△ABD≌△CBD.
∴∠ADB=∠CDB.
A
B
C
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN.
∴四边形MPND是正方形.
A
B
C
D
P
M
N
今天作业
课本P104页第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
