第19章 四边形 复习(2)平行四边形 课件(共28张PPT)
文档属性
| 名称 | 第19章 四边形 复习(2)平行四边形 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 937.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 07:14:15 | ||
图片预览


文档简介
(共28张PPT)
沪科版 八年级下册
第19章 四边形 复习(2)
平行四边形
1.平行四边形的定义是什么?
2.平行四边形具有那些性质?
两组对边分别平行的四边形是平行四边形.
平行四边形的性质
边
角
对角线
对边平行且相等
对角相等
对角线互相平分
邻角互补
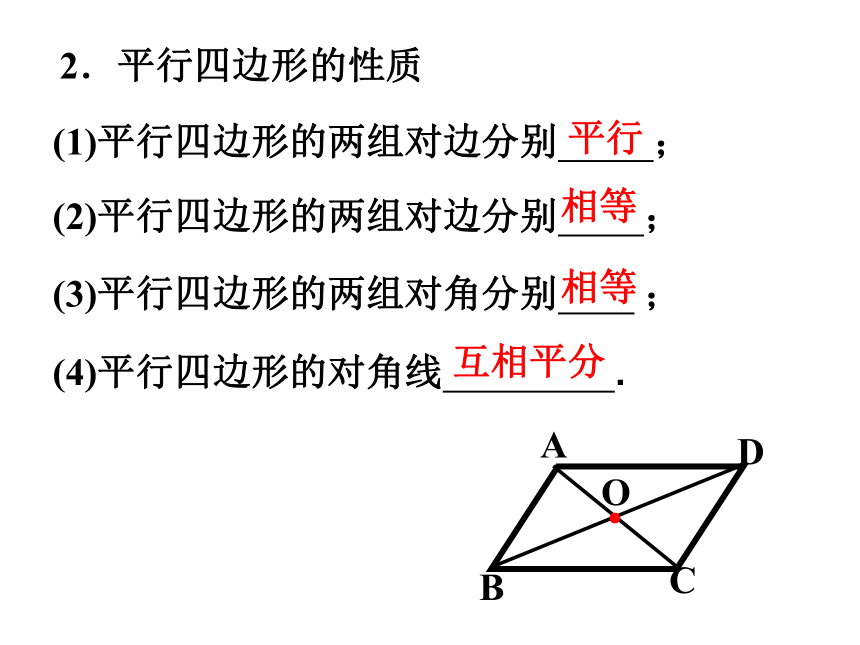
(1)平行四边形的两组对边分别 ;
(2)平行四边形的两组对边分别 ;
(3)平行四边形的两组对角分别 ;
(4)平行四边形的对角线 .
相等
相等
平行
2.平行四边形的性质
互相平分
A
C
D
B
O
●
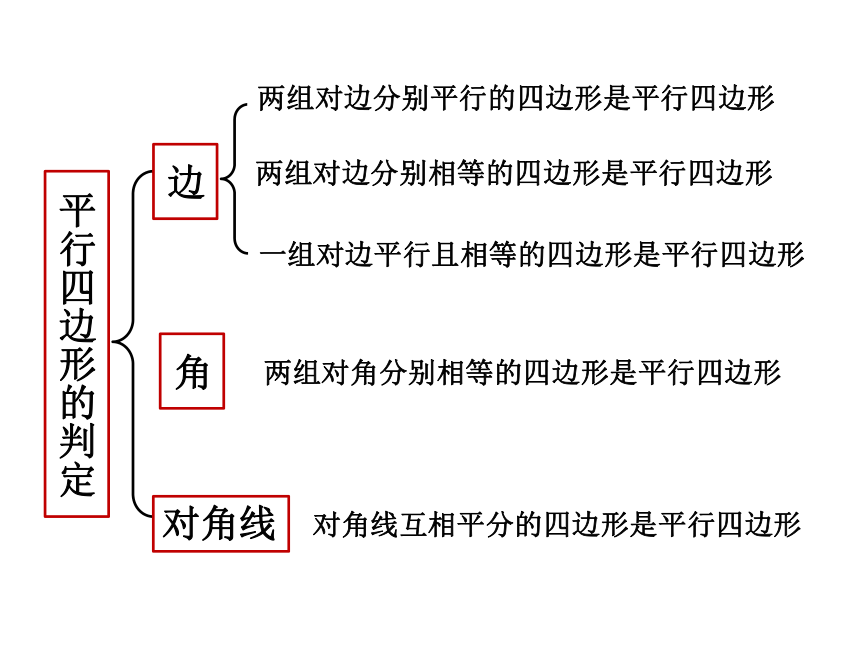
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
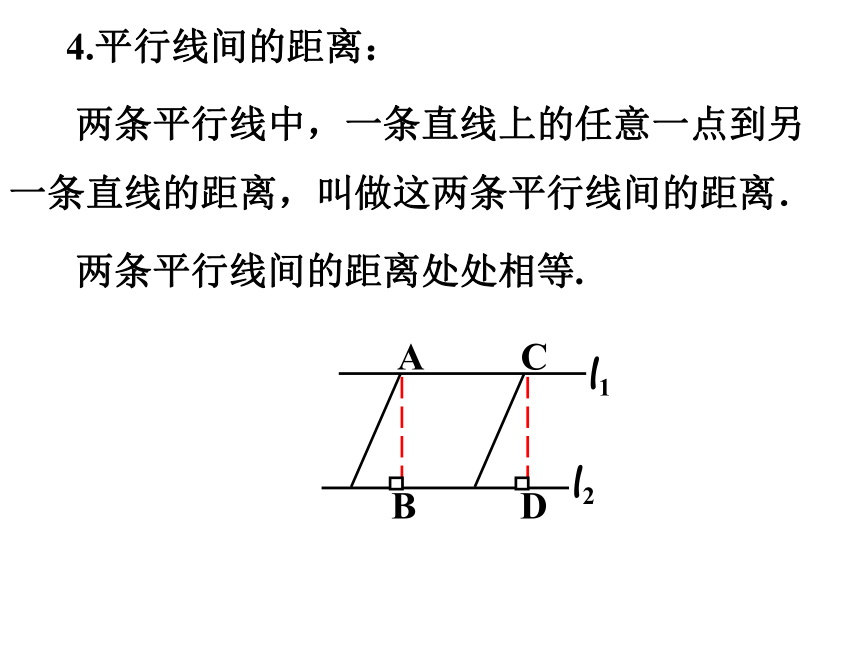
4.平行线间的距离:
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.
两条平行线间的距离处处相等.
A
B
C
D
l1
l2
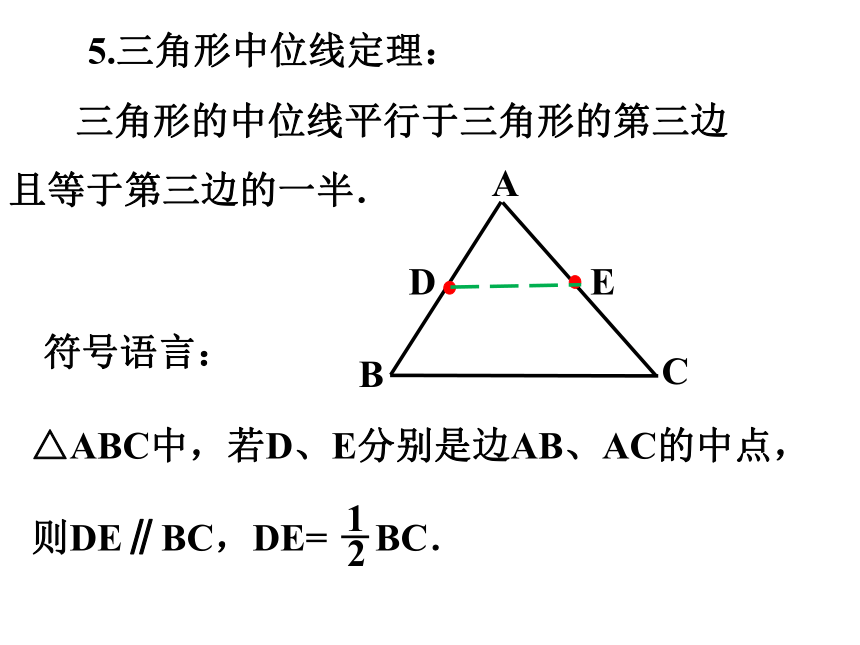
三角形的中位线平行于三角形的第三边
且等于第三边的一半.
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
5.三角形中位线定理:
符号语言:
1
2
A
B
C
D
E
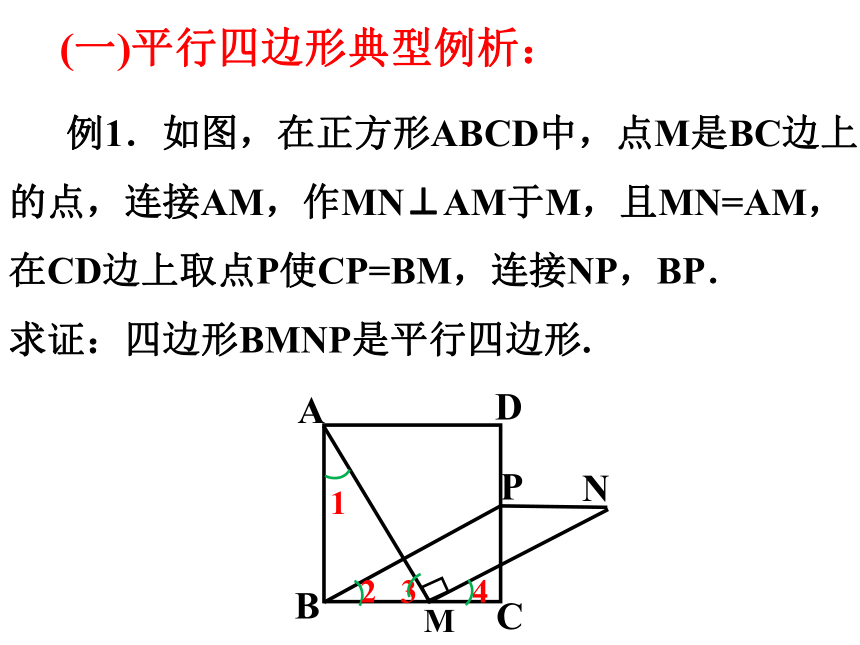
例1.如图,在正方形ABCD中,点M是BC边上的点,连接AM,作MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,连接NP,BP.
求证:四边形BMNP是平行四边形.
A
B
N
C
D
M
P
4
1
3
2
(一)平行四边形典型例析:
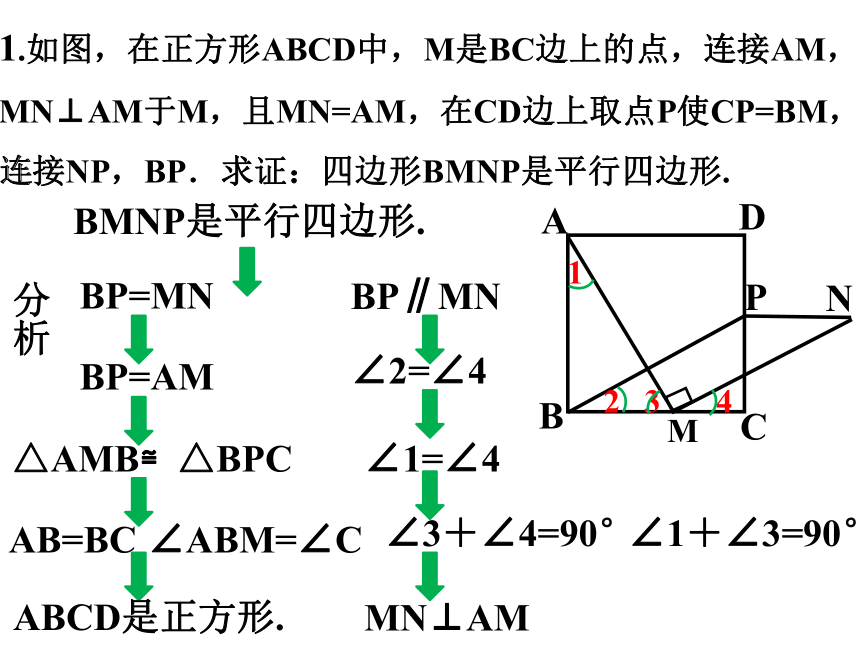
1.如图,在正方形ABCD中,M是BC边上的点,连接AM,MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,
连接NP,BP.求证:四边形BMNP是平行四边形.
A
B
N
C
D
M
P
4
1
3
2
分析
BMNP是平行四边形.
BP∥MN
BP=MN
∠2=∠4
BP=AM
△AMB≌△BPC
AB=BC
∠ABM=∠C
ABCD是正方形.
∠1=∠4
∠3+∠4=90°
∠1+∠3=90°
MN⊥AM
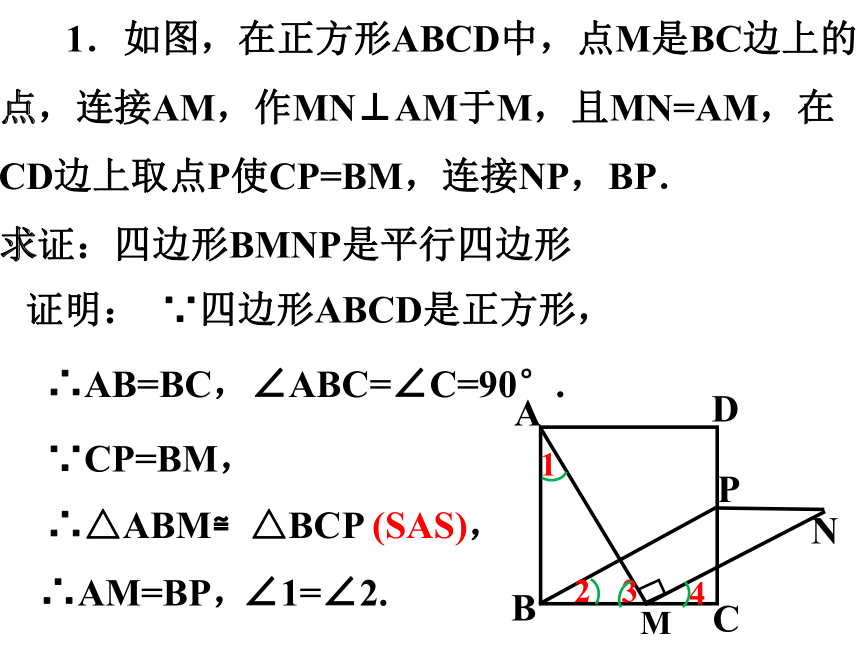
1.如图,在正方形ABCD中,点M是BC边上的点,连接AM,作MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,连接NP,BP.
求证:四边形BMNP是平行四边形
证明:
∵CP=BM,
∴AM=BP,
∴△ABM≌△BCP (SAS),
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∠1=∠2.
A
B
N
C
D
M
P
4
1
3
2
A
B
N
C
D
M
P
4
1
3
∴AB=BC,∠ABC=∠C=90°.
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠1=∠2.
∵ AM⊥MN,且AM=MN,
∴∠3+∠4=90°,
∵∠1+∠3=90°,
∴MN∥BP,
证明:
∵四边形ABCD是正方形,
∵BM=CP,
MN=BP.
∴∠1=∠4,
∴四边形BMNP是平行四边形.
2
∴∠2=∠4,
2. 如图,在□ABCD中, BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD.
求证:四边形AFCE是平行四边形.
要证
要证
要证
要证
要证
四边形AFCE是平行四边形.
AE=CF
AE∥CF
△ABE≌△CDF
AB=CD
∠ABD =∠CDB.
四边形ABCD是平行四边形.
∠AEB =∠CFD
AE⊥BD,
CF⊥BD.
∵四边形ABCD是平行四边形,
∴AB= CD,
AB∥CD.
∴∠1=∠2.
D
A
C
B
E
F
1
2
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD,
∴△AEB≌△CFD.
AE //CF .
∴AE = CF .
∴四边形AECF是平行四边形.
1.在□ABCD中,下列结论一定正确的是( )
A.AC⊥BD B.∠A+∠B=180°
C.AB=AD D.∠A≠∠C
C
D
B
A
B
(二)平行四边形的练习:
2.在□ABCD中,∠A+∠C=200°,则∠B的度数为 ( ).
D
A
C
B
A.100° B.160° C.80° D.60°
C
3.如图,□ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD
A
C
D
B
O
●
1
2
D
4.如图,□ABCD的对角线交于点O,AB=5,△OCD的周长为23,则□ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
A
C
D
B
O
●
C
5. 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是 ( )
A.15° B.20° C.25° D.30°
D
6. 如图,在周长为20cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为 .
A
C
D
B
O
●
E
10cm
7.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2, □ABCD的周长是在14,则DM等于( ).
A.1 B.2 C.3 D.4
D
B
A
C
M
1
2
3
∴∠1=∠2,
∴∠1=∠3,
∴∠2=∠3,
∴MC=BC.
5
C
∵ BM平分∠ABC,
∵AD∥BC,
2
2
2
8.在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( ).
A.5 B. 7 C.9 D.11
A
B
C
D
E
F
B
9.如图,已知:BE∥DF ,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
四边形DEBF是平行四边形.
BE = DF .
△ADF≌△CBE.
∠AFD =∠CEB.
EB //FD.
要证
要证
要证
要证
证明:
∵ BE ∥ DF ,
∴∠AFD=∠CEB.
∵ AF =CE,
∠ADC =∠CBE.
∴△ADF≌△CBE.
∴BE =DF .
∴四边形DEBF是平行四边形.
A
B
C
D
E
F
9.如图,已知:BE∥DF ,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
10. 已知:如图,在□ ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)求证:△DCE≌△FBE;
(2)若EC=3,求AD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠1=∠F,
又 ∵BF=AB,
∴DC=FB,
1
2
3
∵∠2=∠3,
∴△DCE ≌△FBE
(2)∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.
今天作业
课本P103页第4、7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级下册
第19章 四边形 复习(2)
平行四边形
1.平行四边形的定义是什么?
2.平行四边形具有那些性质?
两组对边分别平行的四边形是平行四边形.
平行四边形的性质
边
角
对角线
对边平行且相等
对角相等
对角线互相平分
邻角互补
(1)平行四边形的两组对边分别 ;
(2)平行四边形的两组对边分别 ;
(3)平行四边形的两组对角分别 ;
(4)平行四边形的对角线 .
相等
相等
平行
2.平行四边形的性质
互相平分
A
C
D
B
O
●
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
4.平行线间的距离:
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.
两条平行线间的距离处处相等.
A
B
C
D
l1
l2
三角形的中位线平行于三角形的第三边
且等于第三边的一半.
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
5.三角形中位线定理:
符号语言:
1
2
A
B
C
D
E
例1.如图,在正方形ABCD中,点M是BC边上的点,连接AM,作MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,连接NP,BP.
求证:四边形BMNP是平行四边形.
A
B
N
C
D
M
P
4
1
3
2
(一)平行四边形典型例析:
1.如图,在正方形ABCD中,M是BC边上的点,连接AM,MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,
连接NP,BP.求证:四边形BMNP是平行四边形.
A
B
N
C
D
M
P
4
1
3
2
分析
BMNP是平行四边形.
BP∥MN
BP=MN
∠2=∠4
BP=AM
△AMB≌△BPC
AB=BC
∠ABM=∠C
ABCD是正方形.
∠1=∠4
∠3+∠4=90°
∠1+∠3=90°
MN⊥AM
1.如图,在正方形ABCD中,点M是BC边上的点,连接AM,作MN⊥AM于M,且MN=AM,在CD边上取点P使CP=BM,连接NP,BP.
求证:四边形BMNP是平行四边形
证明:
∵CP=BM,
∴AM=BP,
∴△ABM≌△BCP (SAS),
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°.
∠1=∠2.
A
B
N
C
D
M
P
4
1
3
2
A
B
N
C
D
M
P
4
1
3
∴AB=BC,∠ABC=∠C=90°.
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠1=∠2.
∵ AM⊥MN,且AM=MN,
∴∠3+∠4=90°,
∵∠1+∠3=90°,
∴MN∥BP,
证明:
∵四边形ABCD是正方形,
∵BM=CP,
MN=BP.
∴∠1=∠4,
∴四边形BMNP是平行四边形.
2
∴∠2=∠4,
2. 如图,在□ABCD中, BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD.
求证:四边形AFCE是平行四边形.
要证
要证
要证
要证
要证
四边形AFCE是平行四边形.
AE=CF
AE∥CF
△ABE≌△CDF
AB=CD
∠ABD =∠CDB.
四边形ABCD是平行四边形.
∠AEB =∠CFD
AE⊥BD,
CF⊥BD.
∵四边形ABCD是平行四边形,
∴AB= CD,
AB∥CD.
∴∠1=∠2.
D
A
C
B
E
F
1
2
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD,
∴△AEB≌△CFD.
AE //CF .
∴AE = CF .
∴四边形AECF是平行四边形.
1.在□ABCD中,下列结论一定正确的是( )
A.AC⊥BD B.∠A+∠B=180°
C.AB=AD D.∠A≠∠C
C
D
B
A
B
(二)平行四边形的练习:
2.在□ABCD中,∠A+∠C=200°,则∠B的度数为 ( ).
D
A
C
B
A.100° B.160° C.80° D.60°
C
3.如图,□ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD
A
C
D
B
O
●
1
2
D
4.如图,□ABCD的对角线交于点O,AB=5,△OCD的周长为23,则□ABCD的两条对角线的和是( )
A.18 B.28 C.36 D.46
A
C
D
B
O
●
C
5. 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是 ( )
A.15° B.20° C.25° D.30°
D
6. 如图,在周长为20cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为 .
A
C
D
B
O
●
E
10cm
7.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2, □ABCD的周长是在14,则DM等于( ).
A.1 B.2 C.3 D.4
D
B
A
C
M
1
2
3
∴∠1=∠2,
∴∠1=∠3,
∴∠2=∠3,
∴MC=BC.
5
C
∵ BM平分∠ABC,
∵AD∥BC,
2
2
2
8.在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( ).
A.5 B. 7 C.9 D.11
A
B
C
D
E
F
B
9.如图,已知:BE∥DF ,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
四边形DEBF是平行四边形.
BE = DF .
△ADF≌△CBE.
∠AFD =∠CEB.
EB //FD.
要证
要证
要证
要证
证明:
∵ BE ∥ DF ,
∴∠AFD=∠CEB.
∵ AF =CE,
∠ADC =∠CBE.
∴△ADF≌△CBE.
∴BE =DF .
∴四边形DEBF是平行四边形.
A
B
C
D
E
F
9.如图,已知:BE∥DF ,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
10. 已知:如图,在□ ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)求证:△DCE≌△FBE;
(2)若EC=3,求AD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠1=∠F,
又 ∵BF=AB,
∴DC=FB,
1
2
3
∵∠2=∠3,
∴△DCE ≌△FBE
(2)∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.
今天作业
课本P103页第4、7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
