第19章 四边形 复习(1)多边形 课件(共17张PPT)
文档属性
| 名称 | 第19章 四边形 复习(1)多边形 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 07:16:27 | ||
图片预览





文档简介
(共17张PPT)
沪科版 八年级下册
第19章 四边形 复习(1)
多边形
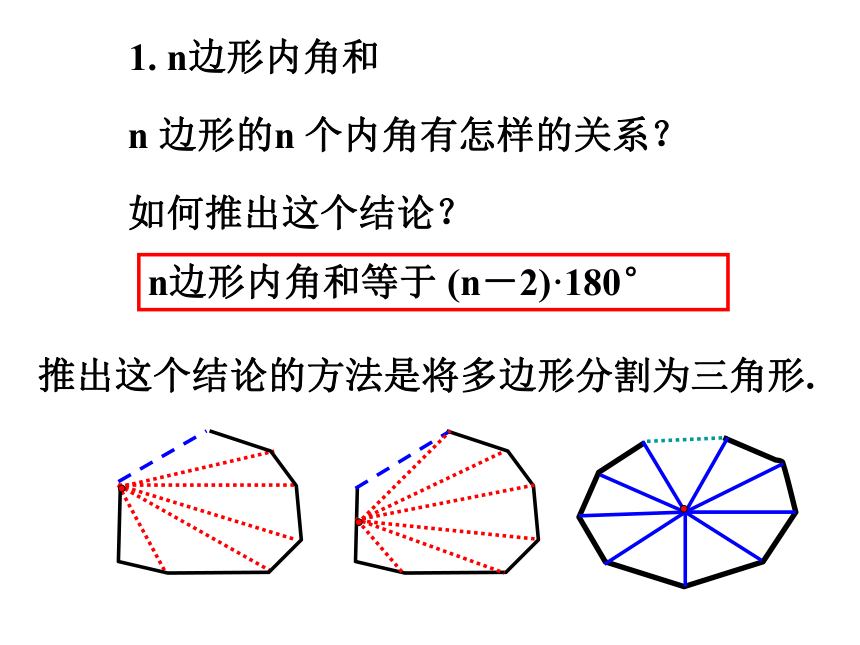
1. n边形内角和
n 边形的n 个内角有怎样的关系?
如何推出这个结论?
n边形内角和等于 (n-2)·180°
推出这个结论的方法是将多边形分割为三角形.
A
1
E
B
C
D
2
3
5
F
n
4
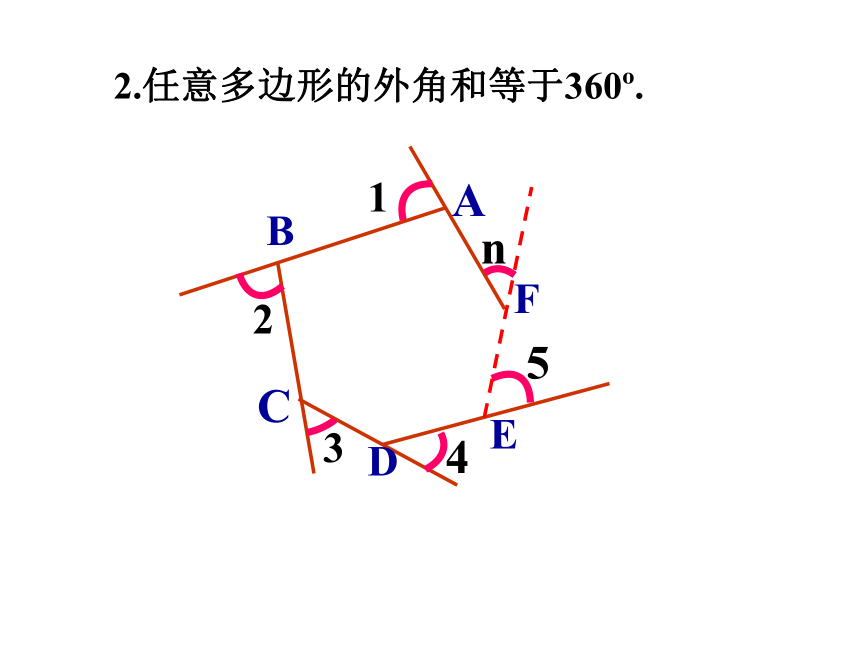
2.任意多边形的外角和等于360 .
1.从10边形的一个顶点画所有的对角线,
一共 能画 条对角线.
2.如果一个多边形的内角和为1260°,
那么从这个多边形的一个顶点出发
共能画 条对角线.
7
6
(一)多边形典型例析:
填空题
3.十二边形的内角和为______,
外角和为_____.
4.已知一个多边形的每一个外角都是72°,
则这个多边形的边数为______.
填空题
1800°
360°
五
5.在五边形ABCDE中,若∠A=∠D=90°,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
解:∵五边形内角和为540°,
∴ ∠B +∠C+∠E
=540°-∠A-∠D
=360°
∴ ∠C=
360°×
2
9
=80°
6.已知一个多边形的各个内角为108° ,
则这个多边形是______边形.
五
(n-2)·180°
=
n·108°
360°
180°-108°
解:
或
7.如果一个多边形的内角和比它的外角和
的3倍少180°,这个多边形的边数是 .
七
(n-2)·180°
360°
×3
-180°
=
(n-2)
=
2×3
-1
解:
8.如图,小亮从A点出发,沿直线前进10米
后向左转30°,再沿直线前进10米,又向
左转30° ……照这样走下去,他第一次
回到出发A点时,一共走了 米.
A
30°
30°
30°
120
1.填空:
(1) 一个多边形的外角和是内角和的 ,
则这个多边形的边数是______.
2
7
9
(n-2)·180°
=360°
2
7
n-2
=7
n=9
(二)多边形的练习:
1.填空:
(2) 一个多边形的每个外角都等于它相邻
的内角, 则这个多边形的边数是____,
它的每个外角的度数是 .
4
90°
2.四边形的内角可能都是锐角吗?
可能都是直角吗?可能都是钝角吗?
答:四边形的内角可能都是直角,
不可能都是锐角或钝角.
都是锐角则内角和小于360°,
都是钝角则内角和大于360°.
设它的每个内角的度数为x,则与它相邻的外角的度数为(180°-x),根据题意,得
答:存在.
3.是否存在一个多边形,它的每个内角都等于
相邻外角的3倍?并简述你的理由.
x=3(180°-x)
它是正八边形.
∴ x=135°
∴ 180° - 135°=45°
∴ 360° ÷ 45°=8
4.一个多边形的内角中,最多有几个锐角?
为什么?
答:一个多边形的内角中,最多有3个锐角.
因为一个多边形的内角中,如果有4个锐角,
则该多边形的外角中有4个钝角,这样外角和就超过360°了.
今天作业
课本P103页第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级下册
第19章 四边形 复习(1)
多边形
1. n边形内角和
n 边形的n 个内角有怎样的关系?
如何推出这个结论?
n边形内角和等于 (n-2)·180°
推出这个结论的方法是将多边形分割为三角形.
A
1
E
B
C
D
2
3
5
F
n
4
2.任意多边形的外角和等于360 .
1.从10边形的一个顶点画所有的对角线,
一共 能画 条对角线.
2.如果一个多边形的内角和为1260°,
那么从这个多边形的一个顶点出发
共能画 条对角线.
7
6
(一)多边形典型例析:
填空题
3.十二边形的内角和为______,
外角和为_____.
4.已知一个多边形的每一个外角都是72°,
则这个多边形的边数为______.
填空题
1800°
360°
五
5.在五边形ABCDE中,若∠A=∠D=90°,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_____.
80°
解:∵五边形内角和为540°,
∴ ∠B +∠C+∠E
=540°-∠A-∠D
=360°
∴ ∠C=
360°×
2
9
=80°
6.已知一个多边形的各个内角为108° ,
则这个多边形是______边形.
五
(n-2)·180°
=
n·108°
360°
180°-108°
解:
或
7.如果一个多边形的内角和比它的外角和
的3倍少180°,这个多边形的边数是 .
七
(n-2)·180°
360°
×3
-180°
=
(n-2)
=
2×3
-1
解:
8.如图,小亮从A点出发,沿直线前进10米
后向左转30°,再沿直线前进10米,又向
左转30° ……照这样走下去,他第一次
回到出发A点时,一共走了 米.
A
30°
30°
30°
120
1.填空:
(1) 一个多边形的外角和是内角和的 ,
则这个多边形的边数是______.
2
7
9
(n-2)·180°
=360°
2
7
n-2
=7
n=9
(二)多边形的练习:
1.填空:
(2) 一个多边形的每个外角都等于它相邻
的内角, 则这个多边形的边数是____,
它的每个外角的度数是 .
4
90°
2.四边形的内角可能都是锐角吗?
可能都是直角吗?可能都是钝角吗?
答:四边形的内角可能都是直角,
不可能都是锐角或钝角.
都是锐角则内角和小于360°,
都是钝角则内角和大于360°.
设它的每个内角的度数为x,则与它相邻的外角的度数为(180°-x),根据题意,得
答:存在.
3.是否存在一个多边形,它的每个内角都等于
相邻外角的3倍?并简述你的理由.
x=3(180°-x)
它是正八边形.
∴ x=135°
∴ 180° - 135°=45°
∴ 360° ÷ 45°=8
4.一个多边形的内角中,最多有几个锐角?
为什么?
答:一个多边形的内角中,最多有3个锐角.
因为一个多边形的内角中,如果有4个锐角,
则该多边形的外角中有4个钝角,这样外角和就超过360°了.
今天作业
课本P103页第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
