北师大版数学八年级上册3.2平面直角坐标系课件(共42张PPT)
文档属性
| 名称 | 北师大版数学八年级上册3.2平面直角坐标系课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 06:38:29 | ||
图片预览






文档简介
(共42张PPT)
欢迎大家!
第三章 位置与坐标
2. 平面直角坐标系(第1课时)
如果课上老师要点一名同学回答问题,但不知道同学们的姓名,我想根据同学们所在的位置来确定,你能帮我解决吗?
我帮老师解决问题
阅读教材,回答下列问题:
1. 平面内 组成
平面直角坐标系, 叫x轴(横轴),
取向 为正方向, 叫y轴(纵轴),
取向 为正方向, x轴和 y轴统称坐标轴。
两轴的交点是 。
这个平面叫 平面。
2. 如何用平面直角坐标系表示平面内的点 ?
3. 如何划分象限?
两条互相垂直且有公共原点的数轴
水平的数轴
右
上
铅直的数轴
原点
坐标
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
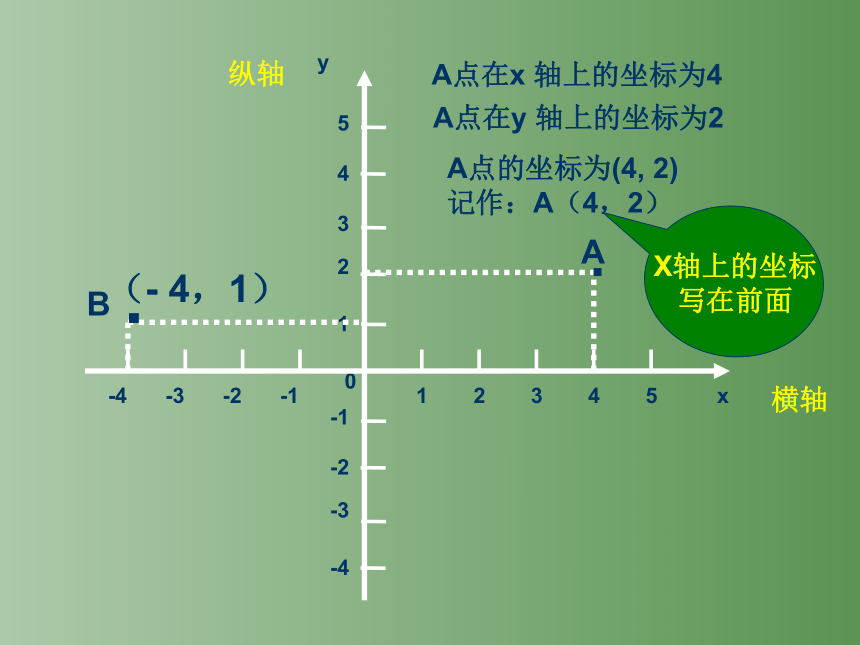
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
(- 4,1)
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
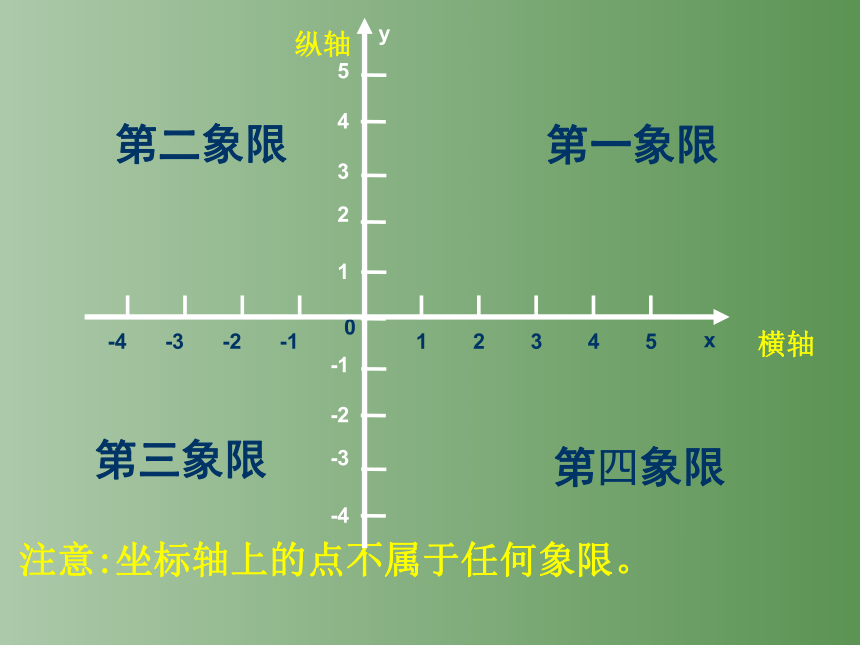
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限。
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
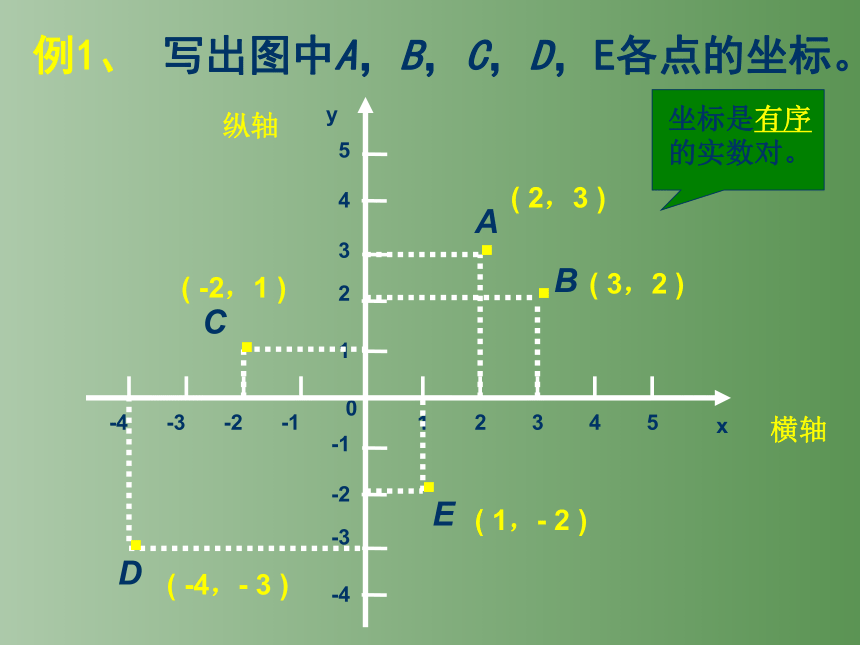
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的实数对。
例1、 写出图中A,B,C,D,E各点的坐标。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
A
·
D
·
C
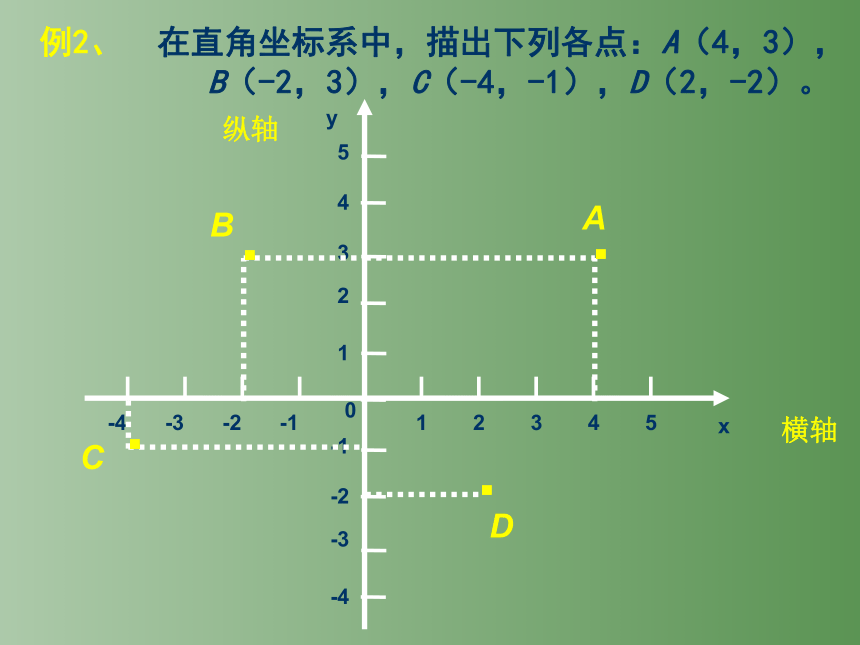
例2、 在直角坐标系中,描出下列各点:A(4,3),
B(-2,3),C(-4,-1),D(2,-2)。
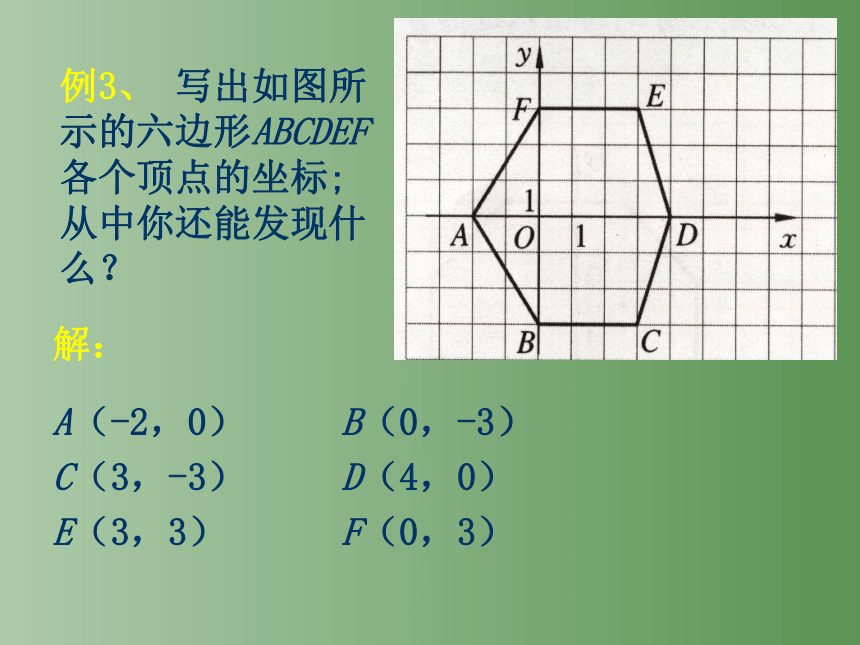
例3、 写出如图所示的六边形ABCDEF各个顶点的坐标;从中你还能发现什么?
解:
A(-2,0) B(0,-3) C(3,-3) D(4,0) E(3,3) F(0,3)
1.平面直角坐标系中,点P(3,5)与Q(5,3)是同一个点吗
2.在平面直角坐标系下,点与实数对之间有何关系?
思考 对比
发现 归纳
在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;
反过来,对于任意一对有序实数对,都有平面上唯一的一点和它对应.
平面内的点与有序实数对是一一对应的。
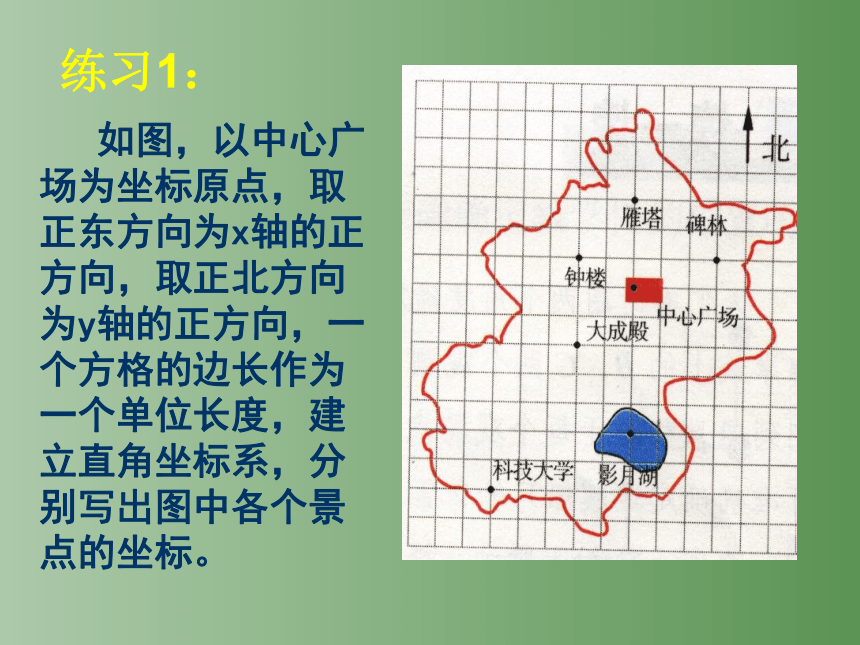
练习1:
如图,以中心广场为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴的正方向,一个方格的边长作为一个单位长度,建立直角坐标系,分别写出图中各个景点的坐标。
如图是学校的示意图,以办公楼所在位置为原点建立平面直角坐标系。
(1)请写出教学楼、实验楼、图书馆的坐标;
(2)学校准备在(-3,-3)处建一栋学生公寓,请你标出学生公寓的位置。
练习2:
拓展练习:
1. 点M(x,y)在第四象限且 求M点的坐标。
2. 点M(x,y)在第二象限,且x+y=2,请写出两个符合条件的M点的坐标。
1. 能够正确画出直角坐标系;
2. 能在直角坐标系中,根据坐标找出点,由点求出坐标;
平面内的点与有序实数对是一一对应的;
3. 掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0);
y轴上的点的横坐标为0,表示为(0,y);
原点的坐标为(0,0)
横坐标相同的点的连线与纵轴平行,
纵坐标相同的点的连线与横轴平行
4.掌握四个象限内点的坐标的特点:
第一象限(+,+);第二象限(-,+)
第三象限(-,-);第四象限(+,-)
小结:
作业布置
教材习题3.2. 1、2、3、4
第三章 位置与坐标
2. 平面直角坐标系(第2课时)
引例:
在直角坐标系中描出下列各点,并将各组内
这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
观察所描出的图形,它像什么?
-1
y
x
A
B
C
D
G
E
F
o
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
连接起来的图形像“房子”
-1
y
x
A
B
C
D
G
E
F
o
解答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段 EC 与 x 轴有什么位置关系?点 E 和点 C 的坐标有什么特点?线段 EC 上其他点的坐标呢?
(3)点 F 和点G 的横坐标有什么共同特点,线段 FG 与 y 轴有怎样的位置关系?
-1
y
x
A
B
C
D
G
E
F
o
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0;
线段 AB 上的点都在 y 轴上,它们的横坐标等于 0.
(2)线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同.
线段 EC 上其他点的纵坐标相同,都是 3.
(3)点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行.
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
归纳 概括
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
1.若点P(m+5,m-2)在x轴上,则m= ;
若点P(m+5,m-2)在y轴上,则m= .
2.已知点A(-3,2),点B(1,4),
(1)若CA平行于x轴,BC平行于y轴,则点C的
坐标是 ;
(2)若CA平行于y轴,BC平行于x轴,则点C的
坐标是 .
运用 巩固
3.已知线段AB=3,AB∥x轴,若A点坐标为
(-1,2),则B点坐标是 .
4.不具体标出这些点,分别判断(1,2),
(-1,-3),(2.,-1),(-3,4)这些点所在的象限,说说你是怎么判断的。
5. 如图所示的笑脸中,
(1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。
(2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。
6.在下图的直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来。
①(2,5),(0,3),(4,3),(2,5)
②(1,3),(-2,0),(6,0),(3,3)
③(1,0),(1,-6),(3,-6),(3,0)
⑴观察所得的图形,你觉得它像什么?
⑵找出图形上位于坐标轴上的点,
你是如何找到的,与同伴交流。
⑶上面各组点中各个点位于哪个
象限,你是如何判断的?
(4)图形上一些点之间具有特
殊的位置关系,找出几对,看
看它们的坐标有何特点?
说说你的发现。
拓展 练习
1.在 y轴上的点的横坐标是( ),在 x轴上的点 的纵坐标是( ).
2.点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( ) .
3. 若点 P(2m - 1,3)在第二象限,则( )
A.m >1/2 B.m <1/2 C.m≥-1/2 D.m ≤1/2
4. 如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于 y轴
C.经过原点 D.以上都不对
5.实数 x,y满足 x + y = 0,则点 P( x,y)在( )
A.原点 B.x轴正半轴 C.第一象限 D.任意位置
6.若 mn = 0,则点 P(m,n)必定在 上.
7.已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为 .
8.点 A 在第一象限,当 m 为 时,
点 A( m + 1,3m - 5)到 x轴的距离是它到y轴距离的一半 .
小结:
通过今天这节课的内容,你学到了什么?
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
3
小 结
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
第一 象限 第二 象限 第三 象限 第四 象限 X轴上 Y轴上 原点
(+,+)
(-,+)
(-,-)
(+,-)
(x,0)
(0,y)
(0,0)
作业:
1. 习题3.3. 学有余力的同学做学习与检测
3. 课上思考题
我学习,我快乐!
我自信,我出色!
我努力,我成功!
第三章 位置与坐标
3.2.平面直角坐标系(3)
探究:如图, 矩形ABCD的长宽分别是6,4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C为坐标原点, 分别以CD , CB所在的直线为x 轴,y 轴建立直角坐标系. 此时C点坐标为(0,0).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6, CB长为4, 可得D,B,A的坐标分别为D(6,0),B(0,4),A(6,4) .
交流:在上面的问题中,还可以用以下方式建立直角坐标系
x
y
0
x
y
0
x
y
0
x
y
0
矩形是轴对称图形,对边平行且相等,四个角都是直角,因此建立直角坐标系时考虑了图形在坐标系中的对称性、图形的边与坐标轴的平行性等要素,所以有多种不同的方式建立直角坐标系。
应用:如图,正三角形ABC的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .
A
B
C
解: 如图,以边AB所在的直线为x 轴,以边AB的中垂线y 轴建立直角坐标系.
由正三角形的性质可知CO= ,正三角形ABC各
个顶点A , B , C的坐标分别为A ( -3 , 0 );B ( 3 , 0 );
C ( 0 , ).
y
x
O
( -3 , 0 )
( 3 , 0 )
( 0 , )
6
3
A
B
C
y
x
0
( -3 , - )
( 3 , - )
( 0 , 0 )
6
交流.在上面的问题中,你还可以怎样建立直角坐标系?
与同伴交流.
总结:
建直角坐标系没有固定不变的方法,要具体问题具体
分析,即使同一问题,原点不同,坐标系也不同,得到的
点的坐标也就不同,但他们的相对位置不变,建立坐标系
的总的原则就是为了解决问题方便。
一般的以图形的某一顶点为坐标原点,以它的一边为坐
标轴建立坐标系。
总结:
建直角坐标系的一般建议:
(1)如果图形有对称中心,可以选对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能多的在坐标轴上。
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志物A,B,并且知道藏宝地点的坐标(4,4),除此外不知道其他信息。如何确定直角坐标系找到“宝藏”?
提示:
连接两个标志点, 作所得线段
的中垂线,并以这条线为横轴.
那如何来确定纵轴
议一议
欢迎大家!
第三章 位置与坐标
2. 平面直角坐标系(第1课时)
如果课上老师要点一名同学回答问题,但不知道同学们的姓名,我想根据同学们所在的位置来确定,你能帮我解决吗?
我帮老师解决问题
阅读教材,回答下列问题:
1. 平面内 组成
平面直角坐标系, 叫x轴(横轴),
取向 为正方向, 叫y轴(纵轴),
取向 为正方向, x轴和 y轴统称坐标轴。
两轴的交点是 。
这个平面叫 平面。
2. 如何用平面直角坐标系表示平面内的点 ?
3. 如何划分象限?
两条互相垂直且有公共原点的数轴
水平的数轴
右
上
铅直的数轴
原点
坐标
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
(- 4,1)
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限。
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
坐标是有序
的实数对。
例1、 写出图中A,B,C,D,E各点的坐标。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
A
·
D
·
C
例2、 在直角坐标系中,描出下列各点:A(4,3),
B(-2,3),C(-4,-1),D(2,-2)。
例3、 写出如图所示的六边形ABCDEF各个顶点的坐标;从中你还能发现什么?
解:
A(-2,0) B(0,-3) C(3,-3) D(4,0) E(3,3) F(0,3)
1.平面直角坐标系中,点P(3,5)与Q(5,3)是同一个点吗
2.在平面直角坐标系下,点与实数对之间有何关系?
思考 对比
发现 归纳
在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;
反过来,对于任意一对有序实数对,都有平面上唯一的一点和它对应.
平面内的点与有序实数对是一一对应的。
练习1:
如图,以中心广场为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴的正方向,一个方格的边长作为一个单位长度,建立直角坐标系,分别写出图中各个景点的坐标。
如图是学校的示意图,以办公楼所在位置为原点建立平面直角坐标系。
(1)请写出教学楼、实验楼、图书馆的坐标;
(2)学校准备在(-3,-3)处建一栋学生公寓,请你标出学生公寓的位置。
练习2:
拓展练习:
1. 点M(x,y)在第四象限且 求M点的坐标。
2. 点M(x,y)在第二象限,且x+y=2,请写出两个符合条件的M点的坐标。
1. 能够正确画出直角坐标系;
2. 能在直角坐标系中,根据坐标找出点,由点求出坐标;
平面内的点与有序实数对是一一对应的;
3. 掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0);
y轴上的点的横坐标为0,表示为(0,y);
原点的坐标为(0,0)
横坐标相同的点的连线与纵轴平行,
纵坐标相同的点的连线与横轴平行
4.掌握四个象限内点的坐标的特点:
第一象限(+,+);第二象限(-,+)
第三象限(-,-);第四象限(+,-)
小结:
作业布置
教材习题3.2. 1、2、3、4
第三章 位置与坐标
2. 平面直角坐标系(第2课时)
引例:
在直角坐标系中描出下列各点,并将各组内
这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
观察所描出的图形,它像什么?
-1
y
x
A
B
C
D
G
E
F
o
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
连接起来的图形像“房子”
-1
y
x
A
B
C
D
G
E
F
o
解答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段 EC 与 x 轴有什么位置关系?点 E 和点 C 的坐标有什么特点?线段 EC 上其他点的坐标呢?
(3)点 F 和点G 的横坐标有什么共同特点,线段 FG 与 y 轴有怎样的位置关系?
-1
y
x
A
B
C
D
G
E
F
o
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0;
线段 AB 上的点都在 y 轴上,它们的横坐标等于 0.
(2)线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同.
线段 EC 上其他点的纵坐标相同,都是 3.
(3)点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行.
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
归纳 概括
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
1.若点P(m+5,m-2)在x轴上,则m= ;
若点P(m+5,m-2)在y轴上,则m= .
2.已知点A(-3,2),点B(1,4),
(1)若CA平行于x轴,BC平行于y轴,则点C的
坐标是 ;
(2)若CA平行于y轴,BC平行于x轴,则点C的
坐标是 .
运用 巩固
3.已知线段AB=3,AB∥x轴,若A点坐标为
(-1,2),则B点坐标是 .
4.不具体标出这些点,分别判断(1,2),
(-1,-3),(2.,-1),(-3,4)这些点所在的象限,说说你是怎么判断的。
5. 如图所示的笑脸中,
(1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。
(2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。
6.在下图的直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来。
①(2,5),(0,3),(4,3),(2,5)
②(1,3),(-2,0),(6,0),(3,3)
③(1,0),(1,-6),(3,-6),(3,0)
⑴观察所得的图形,你觉得它像什么?
⑵找出图形上位于坐标轴上的点,
你是如何找到的,与同伴交流。
⑶上面各组点中各个点位于哪个
象限,你是如何判断的?
(4)图形上一些点之间具有特
殊的位置关系,找出几对,看
看它们的坐标有何特点?
说说你的发现。
拓展 练习
1.在 y轴上的点的横坐标是( ),在 x轴上的点 的纵坐标是( ).
2.点 M(- 8,12)到 x轴的距离是( ),到 y轴的距离是( ) .
3. 若点 P(2m - 1,3)在第二象限,则( )
A.m >1/2 B.m <1/2 C.m≥-1/2 D.m ≤1/2
4. 如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于 y轴
C.经过原点 D.以上都不对
5.实数 x,y满足 x + y = 0,则点 P( x,y)在( )
A.原点 B.x轴正半轴 C.第一象限 D.任意位置
6.若 mn = 0,则点 P(m,n)必定在 上.
7.已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为 .
8.点 A 在第一象限,当 m 为 时,
点 A( m + 1,3m - 5)到 x轴的距离是它到y轴距离的一半 .
小结:
通过今天这节课的内容,你学到了什么?
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
3
小 结
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
第一 象限 第二 象限 第三 象限 第四 象限 X轴上 Y轴上 原点
(+,+)
(-,+)
(-,-)
(+,-)
(x,0)
(0,y)
(0,0)
作业:
1. 习题3.3. 学有余力的同学做学习与检测
3. 课上思考题
我学习,我快乐!
我自信,我出色!
我努力,我成功!
第三章 位置与坐标
3.2.平面直角坐标系(3)
探究:如图, 矩形ABCD的长宽分别是6,4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解: 如图,以点C为坐标原点, 分别以CD , CB所在的直线为x 轴,y 轴建立直角坐标系. 此时C点坐标为(0,0).
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
由CD长为6, CB长为4, 可得D,B,A的坐标分别为D(6,0),B(0,4),A(6,4) .
交流:在上面的问题中,还可以用以下方式建立直角坐标系
x
y
0
x
y
0
x
y
0
x
y
0
矩形是轴对称图形,对边平行且相等,四个角都是直角,因此建立直角坐标系时考虑了图形在坐标系中的对称性、图形的边与坐标轴的平行性等要素,所以有多种不同的方式建立直角坐标系。
应用:如图,正三角形ABC的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .
A
B
C
解: 如图,以边AB所在的直线为x 轴,以边AB的中垂线y 轴建立直角坐标系.
由正三角形的性质可知CO= ,正三角形ABC各
个顶点A , B , C的坐标分别为A ( -3 , 0 );B ( 3 , 0 );
C ( 0 , ).
y
x
O
( -3 , 0 )
( 3 , 0 )
( 0 , )
6
3
A
B
C
y
x
0
( -3 , - )
( 3 , - )
( 0 , 0 )
6
交流.在上面的问题中,你还可以怎样建立直角坐标系?
与同伴交流.
总结:
建直角坐标系没有固定不变的方法,要具体问题具体
分析,即使同一问题,原点不同,坐标系也不同,得到的
点的坐标也就不同,但他们的相对位置不变,建立坐标系
的总的原则就是为了解决问题方便。
一般的以图形的某一顶点为坐标原点,以它的一边为坐
标轴建立坐标系。
总结:
建直角坐标系的一般建议:
(1)如果图形有对称中心,可以选对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能多的在坐标轴上。
在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志物A,B,并且知道藏宝地点的坐标(4,4),除此外不知道其他信息。如何确定直角坐标系找到“宝藏”?
提示:
连接两个标志点, 作所得线段
的中垂线,并以这条线为横轴.
那如何来确定纵轴
议一议
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
