教版八年级数学上册11.2.1三角形的内角(2)课件(共18张PPT)
文档属性
| 名称 | 教版八年级数学上册11.2.1三角形的内角(2)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 459.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 07:10:15 | ||
图片预览






文档简介
(共18张PPT)
11.2三角形的内角(2)
1.探索并掌握直角三角形的性质和判定定理;
2.能用直角三角形的性质和判定定理进行计算和证明.
学习目标
1. 如图,△ABC中,
(1)若∠A=32°,∠B=55°,则∠C= °;
(2)若∠C=90°,则∠A+∠B= °.
90
93
180°-32°-55°=93°
∵∠A+∠B+∠C=180°,∠C=90°,
∴∠A+∠B=180° -∠C=90° .
温故知新
有一个角是直角的三角形是直角三角形. 直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC ”.
直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
∵△ABC中,∠C=90°,
∴∠A+∠B=90°.
探究新知
思考:我们知道,如果一个三角形是直角三角形,那么这个三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
解:是直角三角形,理由是:
如图,在△ABC中,∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=90°,
∴△ABC是直角三角形.
直角三角形的判定定理:有两个角互余的三角形是直角三角形.
1. 在直角三角形中,有一个角为60°,则另一个锐角等于 °;
2. △ABC中,若∠A+∠B=∠C ,则△ABC是 三角形.(填锐角/直角/钝角)
直角
解:∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴ ∠A+∠B=∠C =180°÷2=90°.
90°-60°=30°
30
即时训练
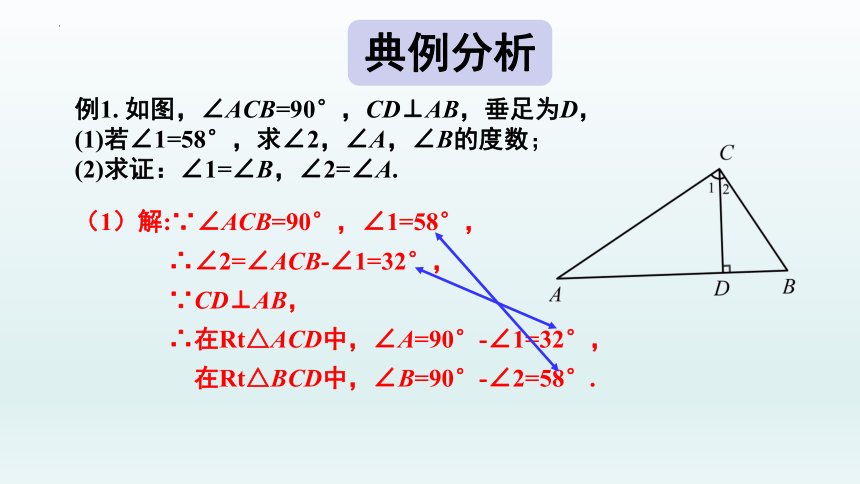
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(1)若∠1=58°,求∠2,∠A,∠B的度数;
(2)求证:∠1=∠B,∠2=∠A.
(1)解:∵∠ACB=90°,∠1=58°,
∴∠2=∠ACB-∠1=32°,
∵CD⊥AB,
∴在Rt△ACD中,∠A=90°-∠1=32°,
在Rt△BCD中,∠B=90°-∠2=58°.
典例分析
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(2)求证:∠1=∠B,∠2=∠A.
思考:①图中有几个直角三角形?
三个:Rt△ABC,Rt△ACD,Rt△BCD;
②图中有几组角互余?
四组:
∠1+∠A=90°,∠A+∠B=90°.
∠1=∠B
∠2=∠A
∠1+∠2=90°,
同角的余角相等
∠B+∠2=90° ,
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(2)求证:∠1=∠B,∠2=∠A.
(2)证明: ∵∠ACB=90°,
∴∠1+∠2=90°,
∵CD⊥AB,
∴∠B +∠2=∠1+∠A =90°,
∴∠1+∠2 =∠B+∠2,∠1+∠2=∠1+∠A,
∴∠1=∠B,∠2=∠A.
特殊 一般
类比推理
如图,CD⊥AB于点D,AF平分∠CAB分别交CD,BC于点E,F,若∠CEF=∠CFE=70°,求证:△ABC为直角三角形.
分析:
证Rt△ABC
∠2+∠3=90 °
∠CAB+∠B=90°
变式应用
∠5+∠6=90°
求∠B,∠CAB,∠3,∠4,∠5,∠6的度数
证∠ACB=90°
证明: ∵∠1=∠2=70°,
∴∠7=∠1=70°,
∵CD⊥AB,
∴∠4=90°-∠7=20°,
∵AF平分∠CAB,
∴∠3=∠4=20°,
∴∠2+∠3=20°+70°=90°,
∴∠ACB=90°,
∴△ABC为直角三角形.
变式应用
如图,CD⊥AB于点D,AF平分∠CAB分别交CD,BC于点E,F,若∠CEF=∠CFE=70°,求证:△ABC为直角三角形.
直角三角形的性质
直角三角形的判断
角平分线的定义
小结
三角形内角和180°
直角三角形的两个锐角互余
高线、角平分线
求角度或
证明角的关系
1. 如图,CD⊥AB,CE平分∠ACB,∠A=30°,∠B=62° ,求∠DCE的度数.
分析:
巩固练习
求∠DCE
∠BCE-∠BCD
90°-∠CED
∠ACD-∠ACE
90°-∠B
90°-∠A
∠ACB
∠A=30°,∠B=62°
180°-∠BCE-∠B
解:∵∠A=30°,∠B=62°,
∴∠ACB =180°-62°-30°=88°,
∵CE平分∠ACB,
∴∠BCE= ∠BCA=44°,
∵CD⊥AB,
∴∠BCD=90°-62°=28°,
∴∠DCE=∠BCE-∠BCD=44°-28°=16°.
巩固练习
1. 如图,CD⊥AB,CE平分∠ACB,∠A=30°,∠B=62°,求∠DCE的度数.
1. 直角三角形的两个锐角互余,
有两个角互余的三角形是直角三角形.
2.
课堂小结
∠1=∠B,∠2=∠A
CD⊥AB,AC⊥BC
三角形内角和180°
直角三角形两锐角互余→求角度或
高线、角平分线 证明角的关系
1. 如图1,在Rt△ABC中,CD是斜边AB上的高,∠BCD=35°,∠A的度数为( ).
(A)55° (B)45° (C)35° (D)25°
2. 如图2,在△ABC中,AB⊥AC,DE∥BC,∠B=46°,则∠AED的度数是( ).
(A)44° (B)46° (C)54° (D)56°
3. 如图3,在△ABC中,D, E分别是AB,AC上一点,BE,CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则∠CFE等于( ).
(A)62° (B)68° (C)78° (D)90°
课后作业
图1
图2
图3
4. 如图4,在Rt△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( ).
(A)35° (B)30° (C)25° (D)20°
5. 如图5,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F.当∠DAC=21°,∠B=25°时,∠DAF的度数为( ).
(A)21° (B)22° (C)25° (D)30°
课后作业
图4
图5
11.2三角形的内角(2)
1.探索并掌握直角三角形的性质和判定定理;
2.能用直角三角形的性质和判定定理进行计算和证明.
学习目标
1. 如图,△ABC中,
(1)若∠A=32°,∠B=55°,则∠C= °;
(2)若∠C=90°,则∠A+∠B= °.
90
93
180°-32°-55°=93°
∵∠A+∠B+∠C=180°,∠C=90°,
∴∠A+∠B=180° -∠C=90° .
温故知新
有一个角是直角的三角形是直角三角形. 直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC ”.
直角三角形的性质:直角三角形的两个锐角互余.
几何语言:
∵△ABC中,∠C=90°,
∴∠A+∠B=90°.
探究新知
思考:我们知道,如果一个三角形是直角三角形,那么这个三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗?
解:是直角三角形,理由是:
如图,在△ABC中,∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=90°,
∴△ABC是直角三角形.
直角三角形的判定定理:有两个角互余的三角形是直角三角形.
1. 在直角三角形中,有一个角为60°,则另一个锐角等于 °;
2. △ABC中,若∠A+∠B=∠C ,则△ABC是 三角形.(填锐角/直角/钝角)
直角
解:∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴ ∠A+∠B=∠C =180°÷2=90°.
90°-60°=30°
30
即时训练
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(1)若∠1=58°,求∠2,∠A,∠B的度数;
(2)求证:∠1=∠B,∠2=∠A.
(1)解:∵∠ACB=90°,∠1=58°,
∴∠2=∠ACB-∠1=32°,
∵CD⊥AB,
∴在Rt△ACD中,∠A=90°-∠1=32°,
在Rt△BCD中,∠B=90°-∠2=58°.
典例分析
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(2)求证:∠1=∠B,∠2=∠A.
思考:①图中有几个直角三角形?
三个:Rt△ABC,Rt△ACD,Rt△BCD;
②图中有几组角互余?
四组:
∠1+∠A=90°,∠A+∠B=90°.
∠1=∠B
∠2=∠A
∠1+∠2=90°,
同角的余角相等
∠B+∠2=90° ,
例1. 如图,∠ACB=90°,CD⊥AB,垂足为D,
(2)求证:∠1=∠B,∠2=∠A.
(2)证明: ∵∠ACB=90°,
∴∠1+∠2=90°,
∵CD⊥AB,
∴∠B +∠2=∠1+∠A =90°,
∴∠1+∠2 =∠B+∠2,∠1+∠2=∠1+∠A,
∴∠1=∠B,∠2=∠A.
特殊 一般
类比推理
如图,CD⊥AB于点D,AF平分∠CAB分别交CD,BC于点E,F,若∠CEF=∠CFE=70°,求证:△ABC为直角三角形.
分析:
证Rt△ABC
∠2+∠3=90 °
∠CAB+∠B=90°
变式应用
∠5+∠6=90°
求∠B,∠CAB,∠3,∠4,∠5,∠6的度数
证∠ACB=90°
证明: ∵∠1=∠2=70°,
∴∠7=∠1=70°,
∵CD⊥AB,
∴∠4=90°-∠7=20°,
∵AF平分∠CAB,
∴∠3=∠4=20°,
∴∠2+∠3=20°+70°=90°,
∴∠ACB=90°,
∴△ABC为直角三角形.
变式应用
如图,CD⊥AB于点D,AF平分∠CAB分别交CD,BC于点E,F,若∠CEF=∠CFE=70°,求证:△ABC为直角三角形.
直角三角形的性质
直角三角形的判断
角平分线的定义
小结
三角形内角和180°
直角三角形的两个锐角互余
高线、角平分线
求角度或
证明角的关系
1. 如图,CD⊥AB,CE平分∠ACB,∠A=30°,∠B=62° ,求∠DCE的度数.
分析:
巩固练习
求∠DCE
∠BCE-∠BCD
90°-∠CED
∠ACD-∠ACE
90°-∠B
90°-∠A
∠ACB
∠A=30°,∠B=62°
180°-∠BCE-∠B
解:∵∠A=30°,∠B=62°,
∴∠ACB =180°-62°-30°=88°,
∵CE平分∠ACB,
∴∠BCE= ∠BCA=44°,
∵CD⊥AB,
∴∠BCD=90°-62°=28°,
∴∠DCE=∠BCE-∠BCD=44°-28°=16°.
巩固练习
1. 如图,CD⊥AB,CE平分∠ACB,∠A=30°,∠B=62°,求∠DCE的度数.
1. 直角三角形的两个锐角互余,
有两个角互余的三角形是直角三角形.
2.
课堂小结
∠1=∠B,∠2=∠A
CD⊥AB,AC⊥BC
三角形内角和180°
直角三角形两锐角互余→求角度或
高线、角平分线 证明角的关系
1. 如图1,在Rt△ABC中,CD是斜边AB上的高,∠BCD=35°,∠A的度数为( ).
(A)55° (B)45° (C)35° (D)25°
2. 如图2,在△ABC中,AB⊥AC,DE∥BC,∠B=46°,则∠AED的度数是( ).
(A)44° (B)46° (C)54° (D)56°
3. 如图3,在△ABC中,D, E分别是AB,AC上一点,BE,CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则∠CFE等于( ).
(A)62° (B)68° (C)78° (D)90°
课后作业
图1
图2
图3
4. 如图4,在Rt△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( ).
(A)35° (B)30° (C)25° (D)20°
5. 如图5,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F.当∠DAC=21°,∠B=25°时,∠DAF的度数为( ).
(A)21° (B)22° (C)25° (D)30°
课后作业
图4
图5
