9.1.2 不等式的性质 课件(共21张PPT)
文档属性
| 名称 | 9.1.2 不等式的性质 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 712.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 13:41:52 | ||
图片预览








文档简介
(共21张PPT)
9.1.2 不等式的性质
七年级数学下册同步(人教版)
第九章
不等式与不等式组
学习目标
1.运用不等式基本性质解不等式,将简单的一元一次不等式转化为“xa”“ x a”的形式。(难点)
2. 初步体验不等式在生活中的应用;(重点)
3.体会探索过程中所应用的归纳和类比方法.
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
回顾旧知
大于向右,小于向左,有等号为实心,无等号为空心.
等式基本性质1:
等式的两边都加上(或减去)同一个数或式子,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
回顾旧知
由a+2=b+2, 能得到a=b?
由0.5a=0.5b, 能得到a=b?
由 -2a= -2b, 能得到a=b?
由a-2=b-2, 能得到a=b?
探究新知
不等式是否具有类似的性质呢?
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
探究新知
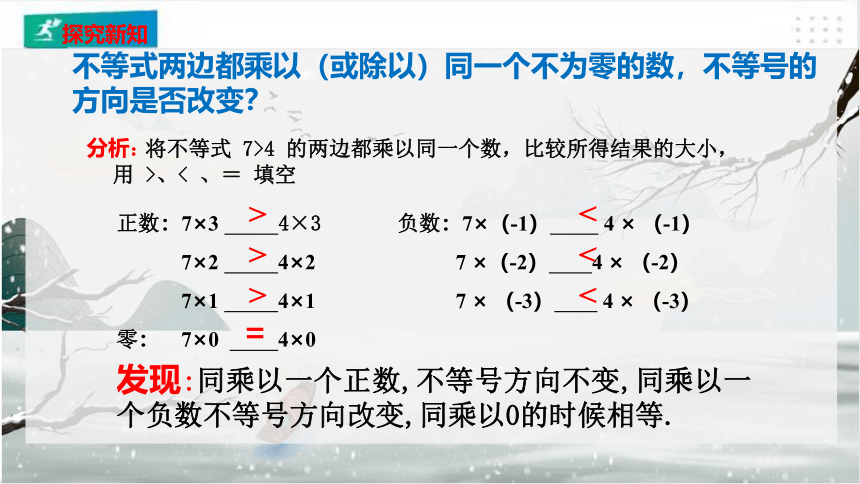
发现:同乘以一个正数,不等号方向不变,同乘以一个负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
分析:
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
探究新知
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac总结归纳
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
巩固提高
2.选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
巩固提高
例1: 用不等式表示下列语句并写出解集, 并在数轴上表示
解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
合作探究
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
合作探究
将下列不等式化成x > a或 x < a 的形式
(1) x-5 > -1
(2) -2x > 4
(3) 7x < 6x -6
解:根据不等式的基本性质1,不等式两边都加上5得x > 4
解:根据不等式的基本性质3 , 不等式两边都除以-2得, x < -2
解:根据不等式的基本性质1,不等式两边都减去6x,得x < -6
合作探究
例2: 小希就读的学校上午第一节课上课时间是早上8点. 小希家距学校有2km, 而她的步行速度为每小时10km. 那么, 小希上午几点从家里出发才能保证不迟到?
解: 设小希上午 x 点从家里出发才能不迟到.
根据题意得
答: 小希上午7:48前时从家里出发才能不迟到.
≤8,
解得 x≤ .
合作探究
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac课堂小结
课堂小结
巧记口诀
加减都用性质1,不等号方向不改变;
乘除正数性质2,不等号方向还不变;
乘除负数性质3,不等号方向必改变
提示:在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题
当堂检测
>
>
<
>
加同一个数,不等号方向不变
减同一个数,不等号方向不变
乘同一个负数,不等号方向改变
除以同一个正数,不等号方向不变
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2D
当堂检测
2. 用不等式表示下列语句并写出解集, 并在数轴上表示 解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
当堂检测
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
当堂检测
https://www.21cnjy.com/help/help_extract.php
9.1.2 不等式的性质
七年级数学下册同步(人教版)
第九章
不等式与不等式组
学习目标
1.运用不等式基本性质解不等式,将简单的一元一次不等式转化为“x
2. 初步体验不等式在生活中的应用;(重点)
3.体会探索过程中所应用的归纳和类比方法.
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
回顾旧知
大于向右,小于向左,有等号为实心,无等号为空心.
等式基本性质1:
等式的两边都加上(或减去)同一个数或式子,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
回顾旧知
由a+2=b+2, 能得到a=b?
由0.5a=0.5b, 能得到a=b?
由 -2a= -2b, 能得到a=b?
由a-2=b-2, 能得到a=b?
探究新知
不等式是否具有类似的性质呢?
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
探究新知
发现:同乘以一个正数,不等号方向不变,同乘以一个负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
分析:
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
探究新知
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
巩固提高
2.选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
巩固提高
例1: 用不等式表示下列语句并写出解集, 并在数轴上表示
解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
合作探究
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
合作探究
将下列不等式化成x > a或 x < a 的形式
(1) x-5 > -1
(2) -2x > 4
(3) 7x < 6x -6
解:根据不等式的基本性质1,不等式两边都加上5得x > 4
解:根据不等式的基本性质3 , 不等式两边都除以-2得, x < -2
解:根据不等式的基本性质1,不等式两边都减去6x,得x < -6
合作探究
例2: 小希就读的学校上午第一节课上课时间是早上8点. 小希家距学校有2km, 而她的步行速度为每小时10km. 那么, 小希上午几点从家里出发才能保证不迟到?
解: 设小希上午 x 点从家里出发才能不迟到.
根据题意得
答: 小希上午7:48前时从家里出发才能不迟到.
≤8,
解得 x≤ .
合作探究
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac
课堂小结
巧记口诀
加减都用性质1,不等号方向不改变;
乘除正数性质2,不等号方向还不变;
乘除负数性质3,不等号方向必改变
提示:在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题
当堂检测
>
>
<
>
加同一个数,不等号方向不变
减同一个数,不等号方向不变
乘同一个负数,不等号方向改变
除以同一个正数,不等号方向不变
加同一个数,不等号方向不变
除以同一个正数,不等号方向不变
乘同一个负数,不等号方向改变
当 m=2,n=-3 时,m2
当堂检测
2. 用不等式表示下列语句并写出解集, 并在数轴上表示 解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
当堂检测
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
当堂检测
https://www.21cnjy.com/help/help_extract.php
