沪科版数学八年级下册 18.1 勾股定理-教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理-教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 00:00:00 | ||
图片预览


文档简介
18.1.1勾股定理
第1课时 勾股定理的探究
教学目标:
1.知识与技能
掌握定理并初步运用勾股定理进行简单运算。
2.过程与方法
在探索勾股定理的过程中,让学生经历观察、猜想、归纳、验证等一系列思维活动,进一步发展学生的思维能力,体会数形结合和从特殊到一般的思考方法。
3.情感、态度与价值观
引导学生阅读中国古代对勾股定理的研究,激发热爱祖国、发奋学习的情怀。
教学重点
掌握勾股定理及其应用。
教学难点
理解勾股定理的发现过程。
教学准备
多媒体课件、方格纸、4个全等的直角三角形。
教学方法
引导发现与启发讲解相结合。
课时:1
教学过程
一、创设情境,引入新课
你见过这个漂亮的图案吗?
回顾直角三角形的特点
(
两个锐角互余
)
(
直角三角形
)
(
直角三
角形的三边
a
、
b
、
c
有没有等量关系呢?
)
探索新知
观察右边两幅图:下图是一个行距和列距都是1的方网格,你能完成下面的表格吗?
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
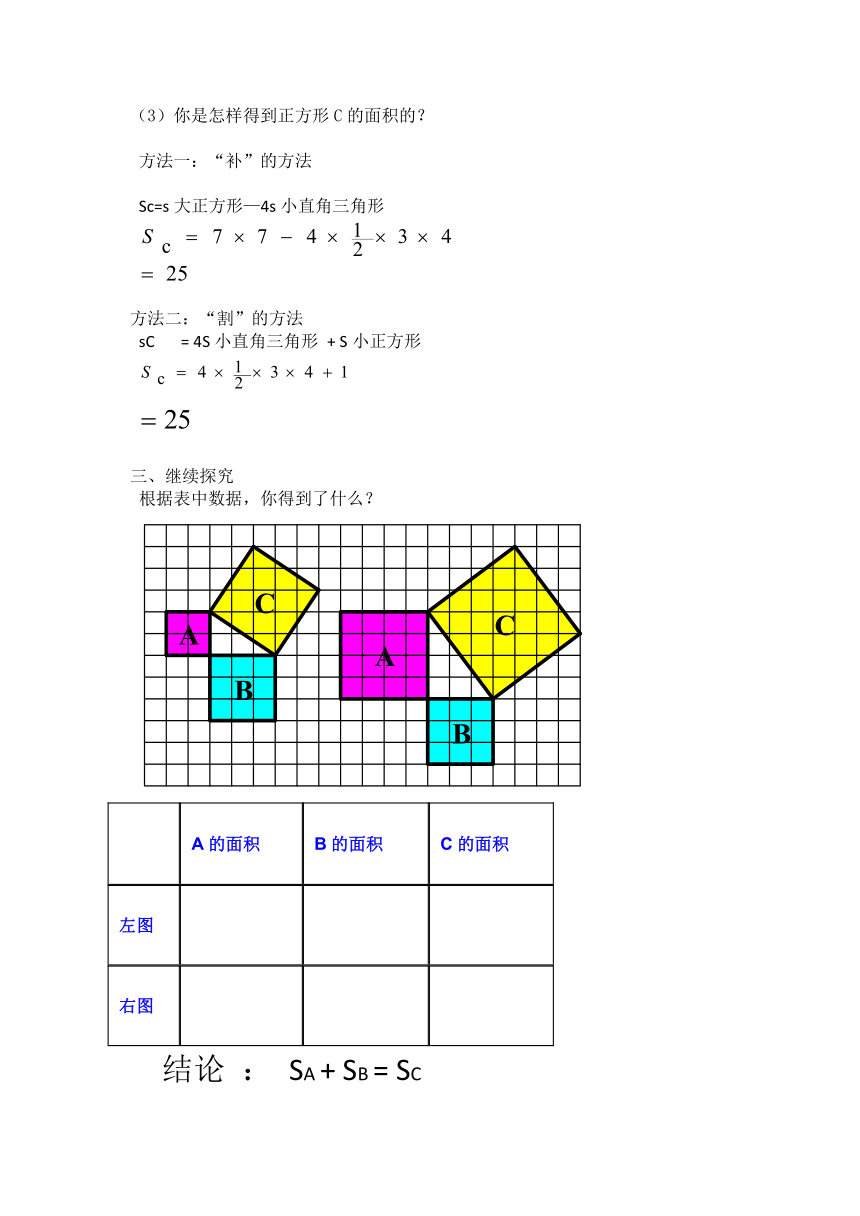
(3)你是怎样得到正方形C的面积的?
方法一:“补”的方法
Sc=s大正方形—4s小直角三角形
方法二:“割”的方法
sC = 4S小直角三角形 + S小正方形
继续探究
根据表中数据,你得到了什么?
A的面积 B的面积 C的面积
左图
右图
结论 : SA + SB = SC
四、继续思考
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
自主证明
如果直角三角形两直角边分别为a、b,斜边为c,
那么
即 直角三角形两直角边的平方和等于斜边的平方.
表示为:Rt△ABC中,∠C=90°,则
勾 股 定 理
如果直角三角形两直角边长分别为a、b,斜边长为c,
那么:
(
a
b
c
)
1.成立条件: 在直角三角形中;
2.公式变形:
3.作用:已知直角三角形任意两边长,
求第三边长.
五、小试身手
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 教材第24页练习第2题.
作业:
请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
六、总结
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
第1课时 勾股定理的探究
教学目标:
1.知识与技能
掌握定理并初步运用勾股定理进行简单运算。
2.过程与方法
在探索勾股定理的过程中,让学生经历观察、猜想、归纳、验证等一系列思维活动,进一步发展学生的思维能力,体会数形结合和从特殊到一般的思考方法。
3.情感、态度与价值观
引导学生阅读中国古代对勾股定理的研究,激发热爱祖国、发奋学习的情怀。
教学重点
掌握勾股定理及其应用。
教学难点
理解勾股定理的发现过程。
教学准备
多媒体课件、方格纸、4个全等的直角三角形。
教学方法
引导发现与启发讲解相结合。
课时:1
教学过程
一、创设情境,引入新课
你见过这个漂亮的图案吗?
回顾直角三角形的特点
(
两个锐角互余
)
(
直角三角形
)
(
直角三
角形的三边
a
、
b
、
c
有没有等量关系呢?
)
探索新知
观察右边两幅图:下图是一个行距和列距都是1的方网格,你能完成下面的表格吗?
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
(3)你是怎样得到正方形C的面积的?
方法一:“补”的方法
Sc=s大正方形—4s小直角三角形
方法二:“割”的方法
sC = 4S小直角三角形 + S小正方形
继续探究
根据表中数据,你得到了什么?
A的面积 B的面积 C的面积
左图
右图
结论 : SA + SB = SC
四、继续思考
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
自主证明
如果直角三角形两直角边分别为a、b,斜边为c,
那么
即 直角三角形两直角边的平方和等于斜边的平方.
表示为:Rt△ABC中,∠C=90°,则
勾 股 定 理
如果直角三角形两直角边长分别为a、b,斜边长为c,
那么:
(
a
b
c
)
1.成立条件: 在直角三角形中;
2.公式变形:
3.作用:已知直角三角形任意两边长,
求第三边长.
五、小试身手
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 教材第24页练习第2题.
作业:
请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
六、总结
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
