10.1.1有限样本空间与随机事件 课件(共15张PPT)
文档属性
| 名称 | 10.1.1有限样本空间与随机事件 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 783.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 16:17:07 | ||
图片预览






文档简介
(共15张PPT)
10.1.1 有限样本空间与随机事件
确定性现象
物体从某个高度开始做自由落体运动时,对下落过程中的每一时刻,下落的高度是唯一确定的.
不确定性现象
抛掷一枚硬币,观察落地时哪面朝上.
抛掷一枚骰子,观察落地时朝上面的点数.
在一批灯管中任意抽取一只,测试它的寿命;
记录某地区7月份的降雨量;
共性:就一次观测而言,出现哪种结果具有偶然性;但在大量重复观测下,各个结果出现的频率却具有稳定性。这类现象叫做随机现象.
把对随机现象的实现和对它的观察称为随机试验,常用字母E表示。
感兴趣的是具有以下特点的随机试验∶
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,
但事先不确定出现哪个结果.
可重复性
可预知性
随机性
研究某种随机现象的规律,首先要观察它所有可能的基本结果.
试验1 抛掷一枚骰子,观察落地时朝上面的点数.
落地时,朝上面的点数有1,2,3,4,5,6共6个可能的基本结果.
可用集合表示为.
样本点:每个可能的基本结果
样本空间:全体样本点的集合
我们用Ω表示样本空间,用ω表示样本点。
如果一个随机试验有n个可能结果,.......
则样本空间为有限样本空间。
试验2 抛掷一枚硬币,观察落地时哪面朝上.
试验的样本空间正面朝上,反面朝上.
如果用h表示“正面朝上”,
t 表示“反面朝上”,
则样本空间可以表示为.
如果用1表示“正面朝上”,
0表示“反面朝上”,
则样本空间可以表示为.
思考:用“1,0”有什么应用价值?
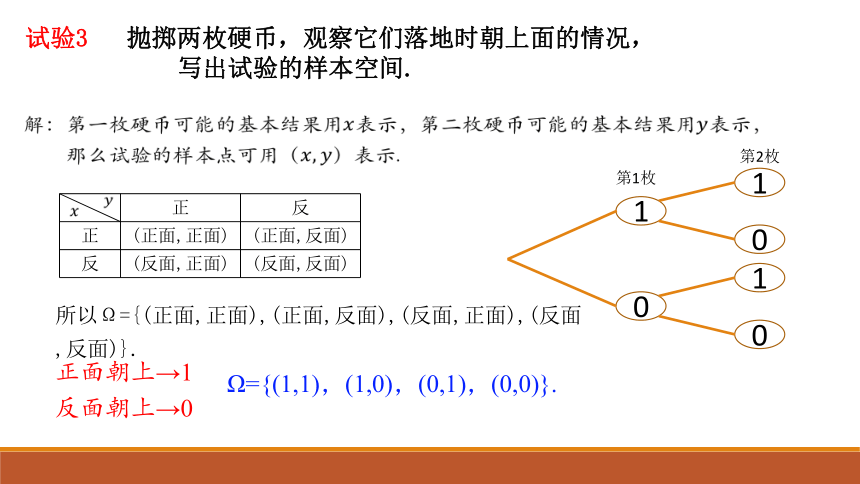
试验3 抛掷两枚硬币,观察它们落地时朝上面的情况,
写出试验的样本空间.
解:第一枚硬币可能的基本结果用表示,第二枚硬币可能的基本结果用表示,
那么试验的样本点可用表示.
所以Ω={(正面,正面),(正面,反面),(反面,正面),(反面,反面)}.
正 反
正 (正面,正面) (正面,反面)
反 (反面,正面) (反面,反面)
正面朝上→1
反面朝上→0
Ω={(1,1),(1,0),(0,1),(0,0)}.
1
1
0
0
1
0
第1枚
第2枚
练习 写出下列各随机试验的样本空间:
(1)采用抽签的方式,随机选择一名同学,并记录其性别;
(2)采用抽签的方式,随机选择一名同学,观察期ABO血型;
(3)随机选择一个有两个小孩的家庭,观察两个孩子的性别;
(4)射击靶3次,观察中靶的次数;
{男,女 }
{A,B,AB,O }
{男男,男女,女男,女女 }
{0,1,2,3 }
思考 在抛掷一枚骰子的试验中:
“朝上面的点数为偶数”是随机事件吗?
如何表示“朝上面的点数为偶数”?
表示“朝上面的点数为偶数”的集合A与样本空间Ω有什么关系?
是
A={2,4,6}
A Ω
一般地,随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示。
为了描述方便,我们将样本空间Ω的子集称为随机事件,简称事件.
一般用大写字母A,B,C……表示
在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生。
只包含一个样本点的事件称为基本事件.
注: Ω为必然事件,为不可能事件.
必然事件与不可能事件不具备随机性.
练习
在10件同类产品中,有7件正品,3件次品,从中任意抽出4件,
下列事件中:
① 4件都是正品; ② 至少有1件是次品;
③ 没有正品; ④ 至少有1件是正品.
其中随机事件有_____,必然事件有___,不可能事件有____.
练习 射击靶3次,观察各次射击中靶或脱靶情况;
(1)写出试验的样本空间;
(2)用集合表示下列事件:
A={中靶2次}
B={至多中靶2次}
例题 一个袋子中有大小和质地相同的5个球,其中有2个红色球(标记为),3个黄色球(标记为),从袋中不放回地依次随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
变式1 一个袋子中有大小和质地相同的5个球,其中有2个红色球,3个黄色球,从袋中有放回地依次随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
变式2 一个袋子中有大小和质地相同的5个球,其中有2个红色球,3个黄色球,从袋中同时随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
课后作业
1、课本243页,习题10.1,第1,2题;
2、课本263页,复习参考题10,第1题;
10.1.1 有限样本空间与随机事件
确定性现象
物体从某个高度开始做自由落体运动时,对下落过程中的每一时刻,下落的高度是唯一确定的.
不确定性现象
抛掷一枚硬币,观察落地时哪面朝上.
抛掷一枚骰子,观察落地时朝上面的点数.
在一批灯管中任意抽取一只,测试它的寿命;
记录某地区7月份的降雨量;
共性:就一次观测而言,出现哪种结果具有偶然性;但在大量重复观测下,各个结果出现的频率却具有稳定性。这类现象叫做随机现象.
把对随机现象的实现和对它的观察称为随机试验,常用字母E表示。
感兴趣的是具有以下特点的随机试验∶
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,
但事先不确定出现哪个结果.
可重复性
可预知性
随机性
研究某种随机现象的规律,首先要观察它所有可能的基本结果.
试验1 抛掷一枚骰子,观察落地时朝上面的点数.
落地时,朝上面的点数有1,2,3,4,5,6共6个可能的基本结果.
可用集合表示为.
样本点:每个可能的基本结果
样本空间:全体样本点的集合
我们用Ω表示样本空间,用ω表示样本点。
如果一个随机试验有n个可能结果,.......
则样本空间为有限样本空间。
试验2 抛掷一枚硬币,观察落地时哪面朝上.
试验的样本空间正面朝上,反面朝上.
如果用h表示“正面朝上”,
t 表示“反面朝上”,
则样本空间可以表示为.
如果用1表示“正面朝上”,
0表示“反面朝上”,
则样本空间可以表示为.
思考:用“1,0”有什么应用价值?
试验3 抛掷两枚硬币,观察它们落地时朝上面的情况,
写出试验的样本空间.
解:第一枚硬币可能的基本结果用表示,第二枚硬币可能的基本结果用表示,
那么试验的样本点可用表示.
所以Ω={(正面,正面),(正面,反面),(反面,正面),(反面,反面)}.
正 反
正 (正面,正面) (正面,反面)
反 (反面,正面) (反面,反面)
正面朝上→1
反面朝上→0
Ω={(1,1),(1,0),(0,1),(0,0)}.
1
1
0
0
1
0
第1枚
第2枚
练习 写出下列各随机试验的样本空间:
(1)采用抽签的方式,随机选择一名同学,并记录其性别;
(2)采用抽签的方式,随机选择一名同学,观察期ABO血型;
(3)随机选择一个有两个小孩的家庭,观察两个孩子的性别;
(4)射击靶3次,观察中靶的次数;
{男,女 }
{A,B,AB,O }
{男男,男女,女男,女女 }
{0,1,2,3 }
思考 在抛掷一枚骰子的试验中:
“朝上面的点数为偶数”是随机事件吗?
如何表示“朝上面的点数为偶数”?
表示“朝上面的点数为偶数”的集合A与样本空间Ω有什么关系?
是
A={2,4,6}
A Ω
一般地,随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示。
为了描述方便,我们将样本空间Ω的子集称为随机事件,简称事件.
一般用大写字母A,B,C……表示
在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生。
只包含一个样本点的事件称为基本事件.
注: Ω为必然事件,为不可能事件.
必然事件与不可能事件不具备随机性.
练习
在10件同类产品中,有7件正品,3件次品,从中任意抽出4件,
下列事件中:
① 4件都是正品; ② 至少有1件是次品;
③ 没有正品; ④ 至少有1件是正品.
其中随机事件有_____,必然事件有___,不可能事件有____.
练习 射击靶3次,观察各次射击中靶或脱靶情况;
(1)写出试验的样本空间;
(2)用集合表示下列事件:
A={中靶2次}
B={至多中靶2次}
例题 一个袋子中有大小和质地相同的5个球,其中有2个红色球(标记为),3个黄色球(标记为),从袋中不放回地依次随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
变式1 一个袋子中有大小和质地相同的5个球,其中有2个红色球,3个黄色球,从袋中有放回地依次随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
变式2 一个袋子中有大小和质地相同的5个球,其中有2个红色球,3个黄色球,从袋中同时随机摸出两个球,观察球的颜色,写出试验的样本空间.
第一次 第二次
课后作业
1、课本243页,习题10.1,第1,2题;
2、课本263页,复习参考题10,第1题;
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
