苏教版六年级下册解决问题的策略课件(共18张PPT)
文档属性
| 名称 | 苏教版六年级下册解决问题的策略课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 20:23:39 | ||
图片预览






文档简介
(共18张PPT)
解决问题的策略
苏教版六年级数学下册
复习
学校美术组中男生人数是女生的 。
1.找出句中的单位“1” ?
2.根据这句话,你能想到什么问题?
根据这句话,我们可以通过转化,用不同的方法来表示男、女人数之间的关系。
今天,我们将继续学习
“解决问题的策略”
例1.星河小学美术组男生人数占总人数的 。
已知女生有21人,男生有多少人?
1.这是一道什么应用题?
2.根据“男生人数占总人数的 ”,可以知道什么?
4.这是我们常见的分数应用题,除了用方程,你还会用其他方法吗?
3.你会列方程解答吗?
解:设星河小学美术组总人数为χ人。
总人数-男生人数=女生人数
χ - χ=21
χ=35
男生人数:35 - 21=14(人)
答:男生有14人。
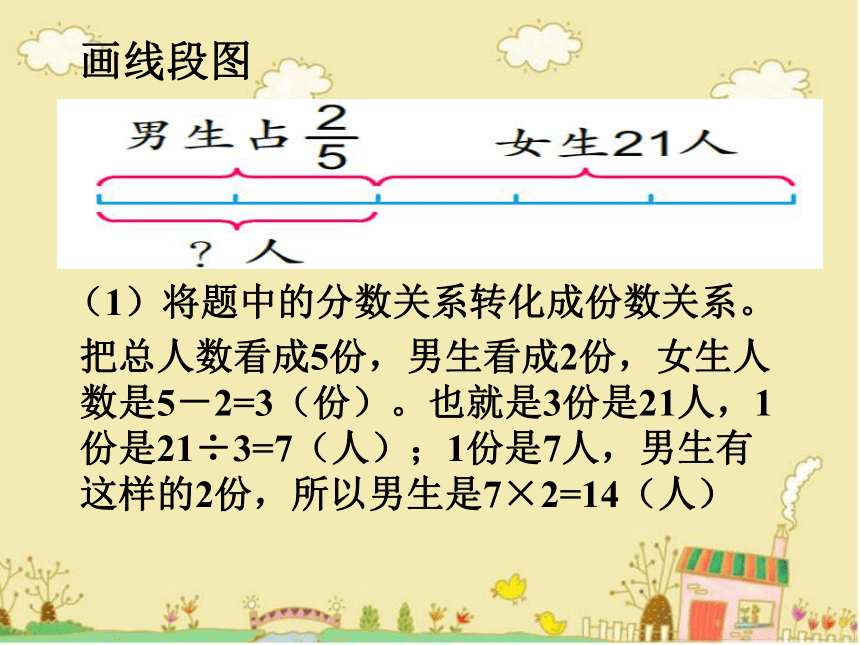
画线段图
(1)将题中的分数关系转化成份数关系。
把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)
男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。
列综合算式:
检验:
14÷(14+21)
=14÷35
=
(2)将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,男生人数与女生人数的比是2 ︰3。
男生人数与女生人数的比是2 ︰3。
男生人数是女生人数的 。
男生人数是女生人数的 。
求一个数是另一个数的几分之几?用乘法计算。
男生人数:21 × =14(人)
答:男生有14人。
列式计算:
总结
解决上面的问题,我们用了解方程的策略、画图的策略和把分数转化成比的策略,在这三种策略中,你觉得哪种策略更适合。
解方程
画图
转化成比
三种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。
2.分数转化成比策略:更容易理解数量之间的关系。
3.解方程策略:可以直观的将题目中的等量关系表现出来。
今天我们主要学习的是画图转化策略,只要画出图来,我们就能很快、很清楚的看出数量关系,列式解答。
归纳总结
现在我们就用画图策略解决一些实际问题。
练习五
2
5
3
5
2
3
7
5
2
7
2
5
课堂总结
同学们,这节课你学习了哪些策略?主要学会了什么策略呢?
解决问题的策略
苏教版六年级数学下册
复习
学校美术组中男生人数是女生的 。
1.找出句中的单位“1” ?
2.根据这句话,你能想到什么问题?
根据这句话,我们可以通过转化,用不同的方法来表示男、女人数之间的关系。
今天,我们将继续学习
“解决问题的策略”
例1.星河小学美术组男生人数占总人数的 。
已知女生有21人,男生有多少人?
1.这是一道什么应用题?
2.根据“男生人数占总人数的 ”,可以知道什么?
4.这是我们常见的分数应用题,除了用方程,你还会用其他方法吗?
3.你会列方程解答吗?
解:设星河小学美术组总人数为χ人。
总人数-男生人数=女生人数
χ - χ=21
χ=35
男生人数:35 - 21=14(人)
答:男生有14人。
画线段图
(1)将题中的分数关系转化成份数关系。
把总人数看成5份,男生看成2份,女生人数是5-2=3(份)。也就是3份是21人,1份是21÷3=7(人);1份是7人,男生有这样的2份,所以男生是7×2=14(人)
男生人数:21 ÷(5 - 2) ×2
=21 ÷3 ×2
=7 ×2
=14(人)
答:男生有14人。
列综合算式:
检验:
14÷(14+21)
=14÷35
=
(2)将题中的分数关系转化成比的关系。
男生人数占总人数的 。
男生人数和总人数的比是2 ︰5,女生人数和总人数的比是3 ︰5,男生人数与女生人数的比是2 ︰3。
男生人数与女生人数的比是2 ︰3。
男生人数是女生人数的 。
男生人数是女生人数的 。
求一个数是另一个数的几分之几?用乘法计算。
男生人数:21 × =14(人)
答:男生有14人。
列式计算:
总结
解决上面的问题,我们用了解方程的策略、画图的策略和把分数转化成比的策略,在这三种策略中,你觉得哪种策略更适合。
解方程
画图
转化成比
三种策略的特点:
1.画图策略:能使数量关系更直观,更清楚。
2.分数转化成比策略:更容易理解数量之间的关系。
3.解方程策略:可以直观的将题目中的等量关系表现出来。
今天我们主要学习的是画图转化策略,只要画出图来,我们就能很快、很清楚的看出数量关系,列式解答。
归纳总结
现在我们就用画图策略解决一些实际问题。
练习五
2
5
3
5
2
3
7
5
2
7
2
5
课堂总结
同学们,这节课你学习了哪些策略?主要学会了什么策略呢?
