沪科版数学八年级下册 18.1 勾股定理课件(共35张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 590.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 08:16:30 | ||
图片预览





文档简介
(共35张PPT)
18.1 勾股定理
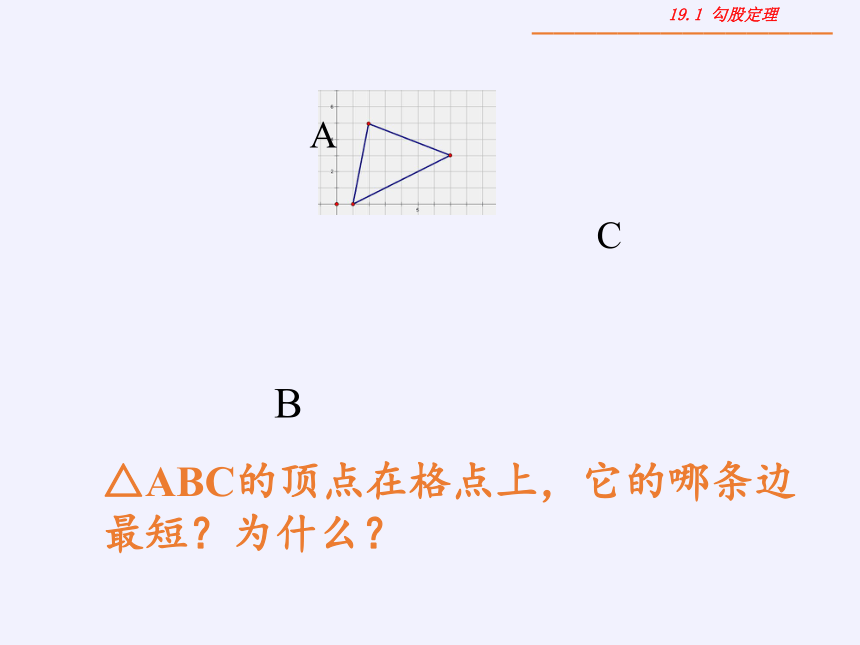
A
B
C
△ABC的顶点在格点上,它的哪条边最短?为什么?
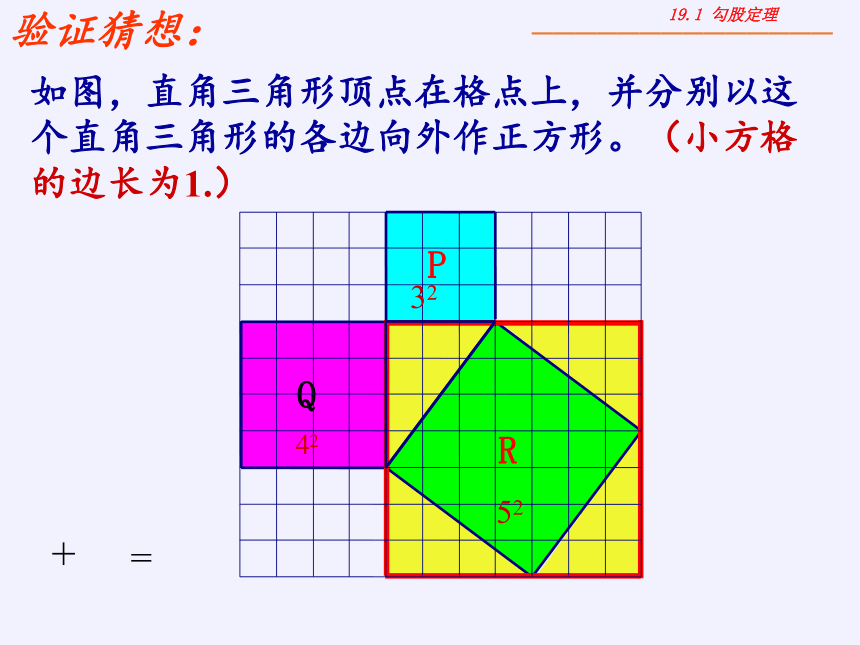
如图,直角三角形顶点在格点上,并分别以这个直角三角形的各边向外作正方形。(小方格的边长为1.)
验证猜想:
P
Q
C
R
32
42
52
+
=
P
Q
C
R
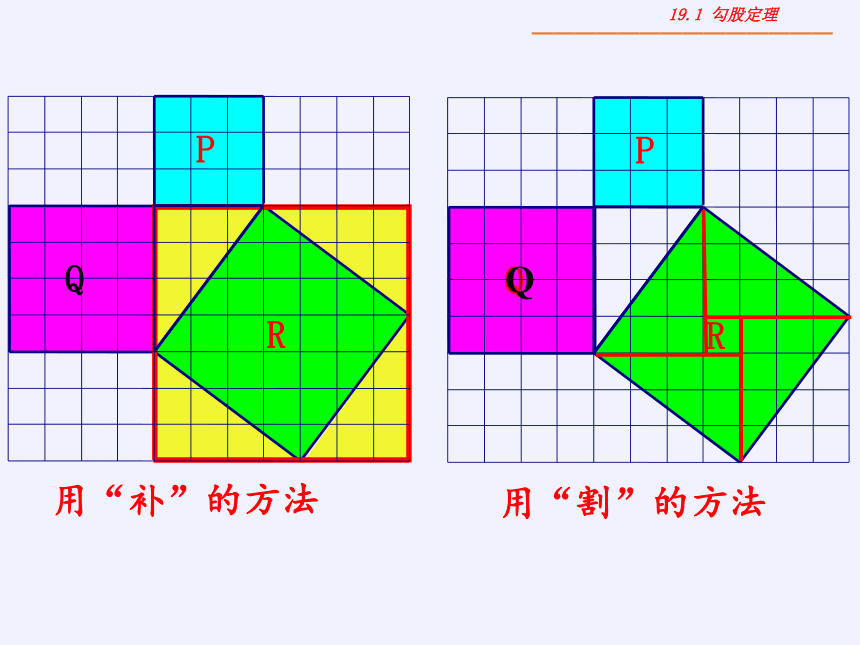
用“补”的方法
P
Q
C
R
用“割”的方法
Q
b
a
b
a
b
a
b
a
c
c
c
c
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
已知:如图,在Rt△ABC中,∠C=90o,AB=c,BC=a,AC=b.
求证: a2 + b2 = c2
b
a
c
A
C
B
勾股定理:
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
∵在Rt△ABC中,∠C=90o
∴AC2+BC2=AB2 或 a2+b2=c2
弦
勾
股
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
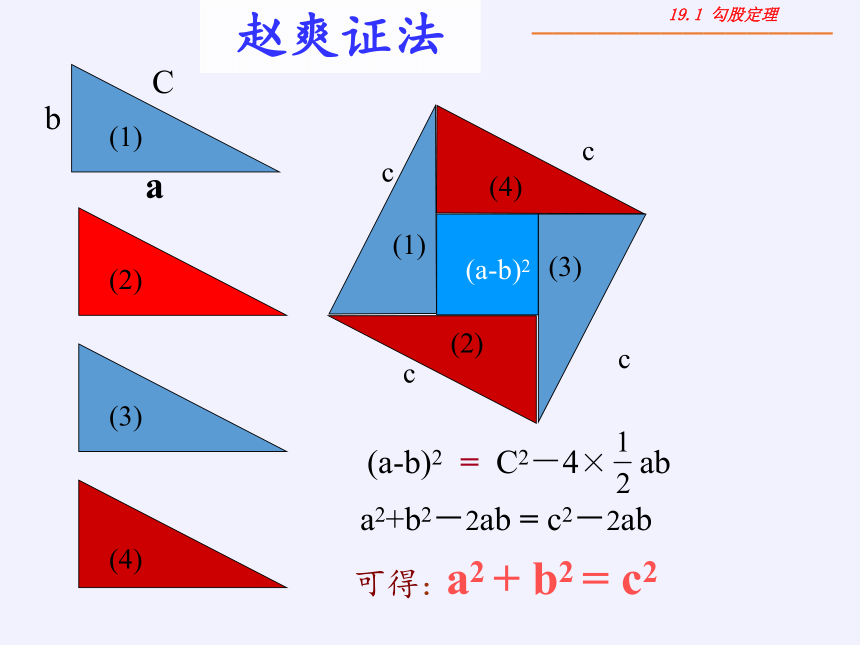
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
赵爽证法
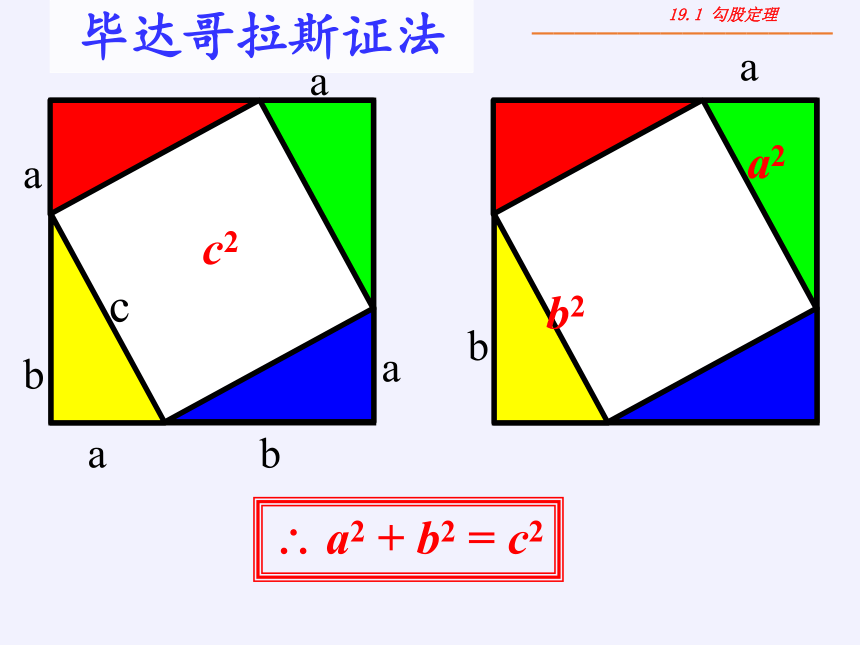
c2
a2
b2
a2 + b2 = c2
毕达哥拉斯证法
c
b
a
b
a
a
a
a
b
1.判断正误:
在△ABC中∠A、∠B、∠C的对边分别是a、b、c,
(1)若a=3, b=4, 则c=5 ( )
(2)若∠B=900,a=3, b=4, 则c=5 ( )
×
×
练一练
2、在直角三角形中,
(1)若两直角边为3、4,则斜边为_____
(2)若一个直角边为5,斜边为13,则另一直角边为_____
练一练
5
12
a
b
c
A
C
B
4
3
A
C
B
4
3
C
A
B
(2)“3”是直角边,“4”是斜边
(1)“3、4”都 是直角边
(3)若两边为3、4,则第三边为_____
D
A
B
C
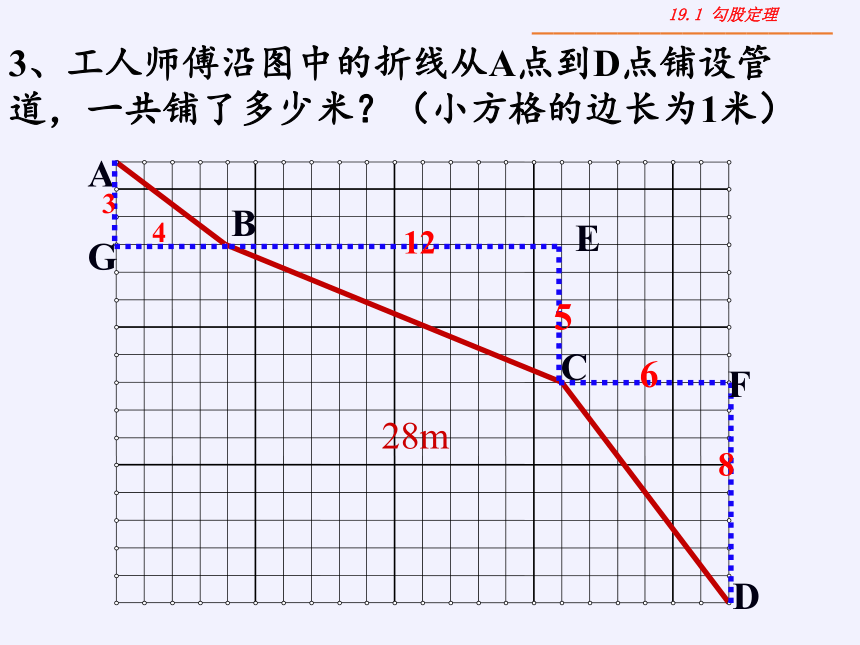
3、工人师傅沿图中的折线从A点到D点铺设管道,一共铺了多少米?(小方格的边长为1米)
G
F
E
3
4
12
5
6
8
28m
A
B
C
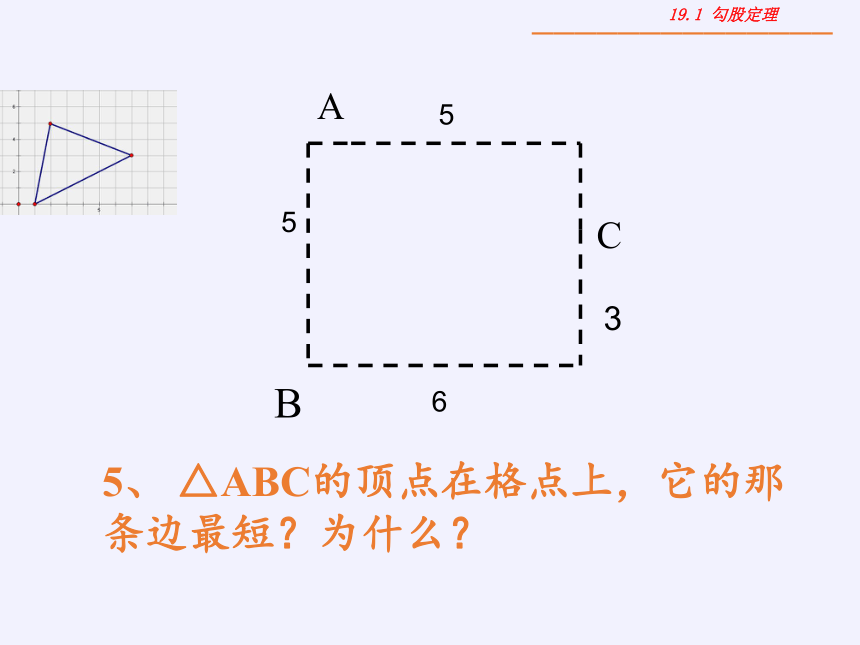
5、 △ABC的顶点在格点上,它的那条边最短?为什么?
5
5
6
3
6、 甲、乙两位探险者到沙漠进行探险.某日早晨甲乙先同时出发,甲以4千米/小时的速度向东行走, 乙以3千米/小时的速度向北行进,两小时后甲、乙二人相距多远
东
北
甲
乙
通过这节课的学习:
你有什么收获?
说说你的体验。
作业
查阅其他证明方法。
你自己设计一种方案验证勾股定理。
请各位老师批评指正
在网格纸上画出Rt△ABC,∠C=900
1、测量出三条边a、b、c的长(精确到毫米)。
2、填空: a2+b2=____,c2=_____.
3、你有什么发现?
A
B
C
合作探究:
a
b
c
3、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)
60
C
20
A
B
A
C
O
B
D
4、一个5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑2m,那么梯子底端B向外移多少
想一想:
大胆猜想:
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
A
B
C
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股世界
数学史
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕长只有58厘米和宽46厘米,他认为是售货员搞错了。你同意他的看法吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,对角线怎么求?
例
46
58
?
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
解:∵
议一议
∴荧屏对角线大约为74厘米
46
58
能力提升:
1、在Rt△ABC中,斜边AB=2,则 AB2+BC2+AC2=____________
2、在直角三角形中,若其中两边长分别为3和5,则它的面积为_______
3、如图,△ABC中,∠C=90°,
CD ⊥AB 于D, AC=9,BC=12,
求:CD的长。
B
A
C
D
2AB2=8
6或7.5
9
12
15
方法(面积法):1/2ACxBC=1/2ABxCD即1/2X9x12=1/2x15xCD所以CD=7.2
◆如图,以Rt△ABC的三边为直径的3个半圆的面积有什么关系 请你说明理由.
练一练
S1
S2
S3
(图中每个小方格代表一个单位面积)
A
B
C
D
F
E
思考:
1、观察左图中的△ABC和△DEF,它们是直角三角形吗?
2、分别以ABC和DEF的各边为一边向外所作的正方形,其中两个小正方形的面积和等于大正方形的面积吗?
S1
S2
S3
S1
S2
S3
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
学以致用
1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
2、已知: c =13,a=5,
求阴影部分的面积。
a
c
b
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3千米处,过了20秒,飞机距离这个男孩头顶5千米。这一过程中飞机飞过的距离是多少千米?
A
B
C
3千米
5千米
20秒后
规范运用
以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
A
B
C
D
E
F
议一议
已知:△ABC,AB=AC=17,BC=16.
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
例题分析
8
17
1、已知:△ABC,AB=AC=17,BC=16,则高AD=_,S△ABC=_.
2、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)
拓展延伸
60
C
20
A
B
美国第二十任总统伽菲尔德的证法:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
整体角度
局部角度
赵爽证法
谢 谢
18.1 勾股定理
A
B
C
△ABC的顶点在格点上,它的哪条边最短?为什么?
如图,直角三角形顶点在格点上,并分别以这个直角三角形的各边向外作正方形。(小方格的边长为1.)
验证猜想:
P
Q
C
R
32
42
52
+
=
P
Q
C
R
用“补”的方法
P
Q
C
R
用“割”的方法
Q
b
a
b
a
b
a
b
a
c
c
c
c
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
已知:如图,在Rt△ABC中,∠C=90o,AB=c,BC=a,AC=b.
求证: a2 + b2 = c2
b
a
c
A
C
B
勾股定理:
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
∵在Rt△ABC中,∠C=90o
∴AC2+BC2=AB2 或 a2+b2=c2
弦
勾
股
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
赵爽证法
c2
a2
b2
a2 + b2 = c2
毕达哥拉斯证法
c
b
a
b
a
a
a
a
b
1.判断正误:
在△ABC中∠A、∠B、∠C的对边分别是a、b、c,
(1)若a=3, b=4, 则c=5 ( )
(2)若∠B=900,a=3, b=4, 则c=5 ( )
×
×
练一练
2、在直角三角形中,
(1)若两直角边为3、4,则斜边为_____
(2)若一个直角边为5,斜边为13,则另一直角边为_____
练一练
5
12
a
b
c
A
C
B
4
3
A
C
B
4
3
C
A
B
(2)“3”是直角边,“4”是斜边
(1)“3、4”都 是直角边
(3)若两边为3、4,则第三边为_____
D
A
B
C
3、工人师傅沿图中的折线从A点到D点铺设管道,一共铺了多少米?(小方格的边长为1米)
G
F
E
3
4
12
5
6
8
28m
A
B
C
5、 △ABC的顶点在格点上,它的那条边最短?为什么?
5
5
6
3
6、 甲、乙两位探险者到沙漠进行探险.某日早晨甲乙先同时出发,甲以4千米/小时的速度向东行走, 乙以3千米/小时的速度向北行进,两小时后甲、乙二人相距多远
东
北
甲
乙
通过这节课的学习:
你有什么收获?
说说你的体验。
作业
查阅其他证明方法。
你自己设计一种方案验证勾股定理。
请各位老师批评指正
在网格纸上画出Rt△ABC,∠C=900
1、测量出三条边a、b、c的长(精确到毫米)。
2、填空: a2+b2=____,c2=_____.
3、你有什么发现?
A
B
C
合作探究:
a
b
c
3、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)
60
C
20
A
B
A
C
O
B
D
4、一个5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑2m,那么梯子底端B向外移多少
想一想:
大胆猜想:
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
A
B
C
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股世界
数学史
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕长只有58厘米和宽46厘米,他认为是售货员搞错了。你同意他的看法吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,对角线怎么求?
例
46
58
?
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
解:∵
议一议
∴荧屏对角线大约为74厘米
46
58
能力提升:
1、在Rt△ABC中,斜边AB=2,则 AB2+BC2+AC2=____________
2、在直角三角形中,若其中两边长分别为3和5,则它的面积为_______
3、如图,△ABC中,∠C=90°,
CD ⊥AB 于D, AC=9,BC=12,
求:CD的长。
B
A
C
D
2AB2=8
6或7.5
9
12
15
方法(面积法):1/2ACxBC=1/2ABxCD即1/2X9x12=1/2x15xCD所以CD=7.2
◆如图,以Rt△ABC的三边为直径的3个半圆的面积有什么关系 请你说明理由.
练一练
S1
S2
S3
(图中每个小方格代表一个单位面积)
A
B
C
D
F
E
思考:
1、观察左图中的△ABC和△DEF,它们是直角三角形吗?
2、分别以ABC和DEF的各边为一边向外所作的正方形,其中两个小正方形的面积和等于大正方形的面积吗?
S1
S2
S3
S1
S2
S3
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
学以致用
1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
2、已知: c =13,a=5,
求阴影部分的面积。
a
c
b
例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3千米处,过了20秒,飞机距离这个男孩头顶5千米。这一过程中飞机飞过的距离是多少千米?
A
B
C
3千米
5千米
20秒后
规范运用
以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
A
B
C
D
E
F
议一议
已知:△ABC,AB=AC=17,BC=16.
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
例题分析
8
17
1、已知:△ABC,AB=AC=17,BC=16,则高AD=_,S△ABC=_.
2、池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m。你能求出A、B两点间的距离吗?(结果保留整数)
拓展延伸
60
C
20
A
B
美国第二十任总统伽菲尔德的证法:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
整体角度
局部角度
赵爽证法
谢 谢
