沪科版数学八年级下册 19.1 多边形内角和 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.1 多边形内角和 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 535.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
19.1 多边形内角和
观察下列图案
三角形
四边形
六边形
三角形
六边形
四边形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
五边形
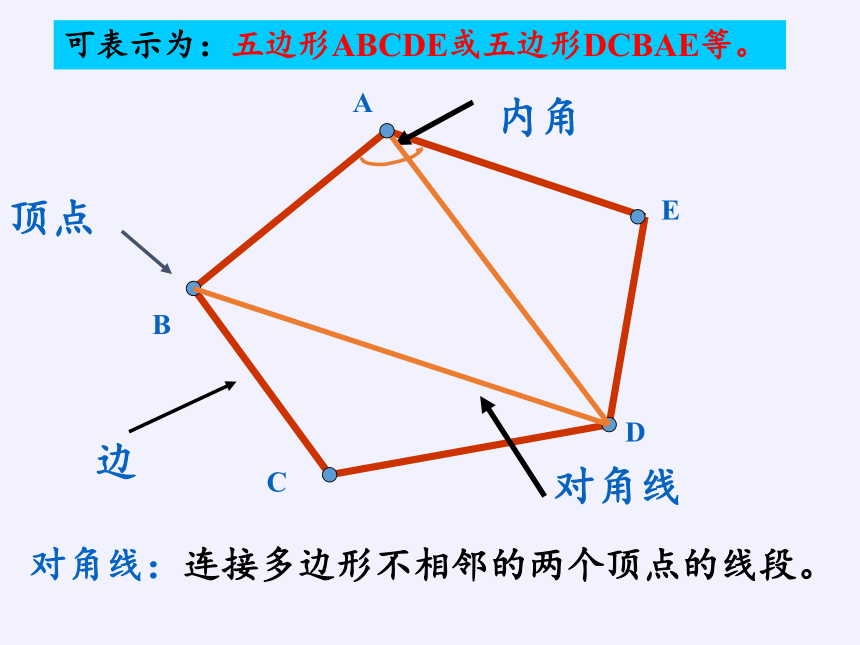
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE等。
A
B
C
D
E
1
2
3
4
5
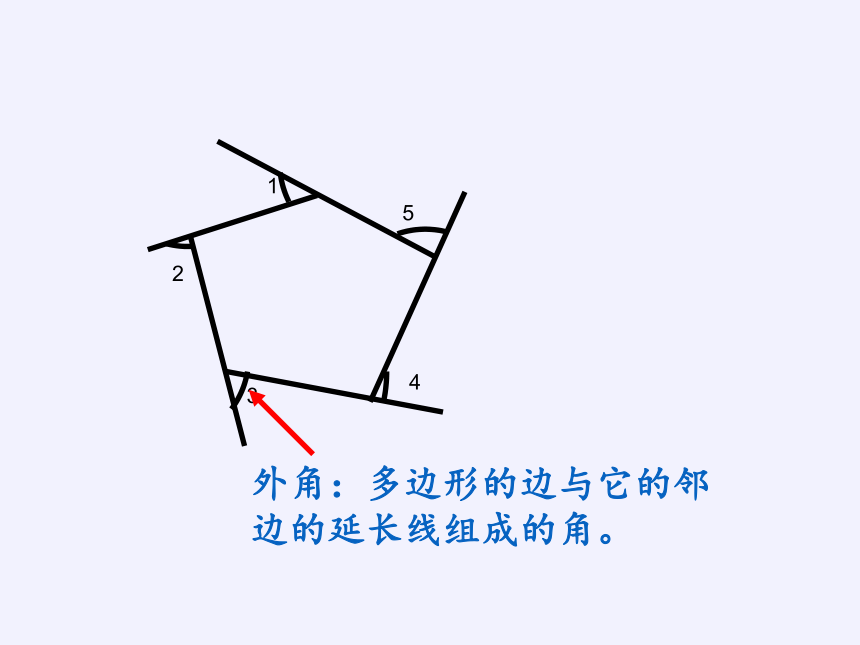
外角:多边形的边与它的邻边的延长线组成的角。
A
B
C
D
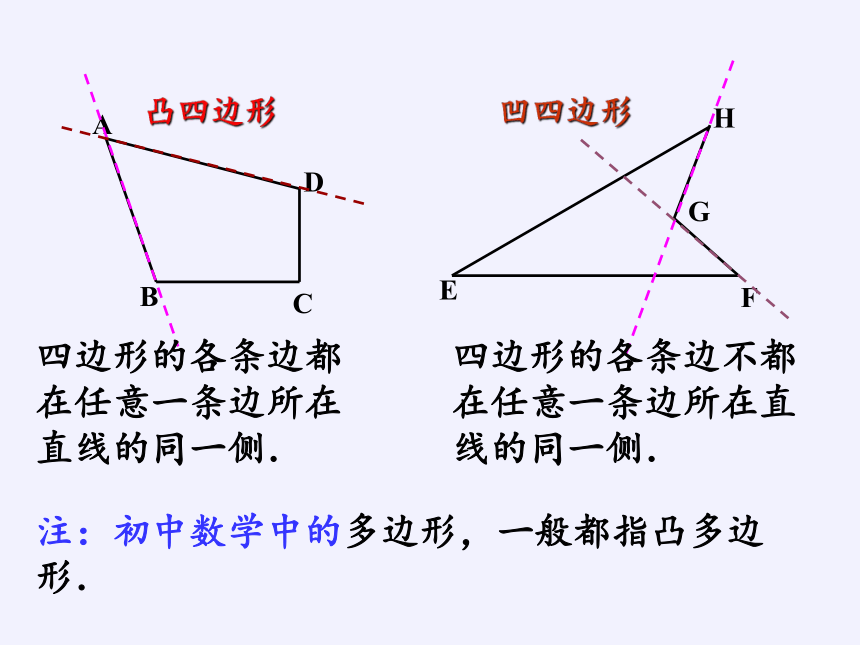
凸四边形
E
F
G
H
凹四边形
注:初中数学中的多边形,一般都指凸多边形.
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
1800
回顾:三角形的内角和是_____.
正方形、长方形的内角和是_____.
3600
任意四边形的内角和是
2×180 °=360°
A
B
C
D
360°
从顶点A可以画 条对角线。
五边形被分成了 个三角形。
A
B
D
C
E
你能用以上方法求出五边形的内角和吗?
180°×3=540°
边数 4 5 6 7 … n
图形
过一顶点对角线条数
分成的三角形个数 …
多边形内角和 …
n边形的内角和等于(n-2).180°
定理:
还有其他方法吗?
A
B
C
D
O
4×180°-360°=360°。
结论:任意四边形的内角和是360 0
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
还有什么方法求多边形的内角和?
1、求十边形的内角和的度数。
2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
知识应用
解:设这个多边形的边数为n,
可列方程(n-2)×180°= 1080°.
解得n=8
答:这个多边形是八边形。
3、小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
4、已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是 。
144°
这节课学习了什么?
n边形的内角和等于(n-2).180°
A
B
C
D
A
B
C
D
O
证明思路:
多边形
三角形
转化
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,能求出n边形的内角和吗?请同学们课后试一试。
课后探究
谢 谢
19.1 多边形内角和
观察下列图案
三角形
四边形
六边形
三角形
六边形
四边形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
五边形
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE等。
A
B
C
D
E
1
2
3
4
5
外角:多边形的边与它的邻边的延长线组成的角。
A
B
C
D
凸四边形
E
F
G
H
凹四边形
注:初中数学中的多边形,一般都指凸多边形.
四边形的各条边都在任意一条边所在直线的同一侧.
四边形的各条边不都在任意一条边所在直线的同一侧.
1800
回顾:三角形的内角和是_____.
正方形、长方形的内角和是_____.
3600
任意四边形的内角和是
2×180 °=360°
A
B
C
D
360°
从顶点A可以画 条对角线。
五边形被分成了 个三角形。
A
B
D
C
E
你能用以上方法求出五边形的内角和吗?
180°×3=540°
边数 4 5 6 7 … n
图形
过一顶点对角线条数
分成的三角形个数 …
多边形内角和 …
n边形的内角和等于(n-2).180°
定理:
还有其他方法吗?
A
B
C
D
O
4×180°-360°=360°。
结论:任意四边形的内角和是360 0
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
还有什么方法求多边形的内角和?
1、求十边形的内角和的度数。
2、若一个多边形的内角和是1080°,求这个多边形的边数。
解:(10-2)×180°
=1440°
答:十边形的内角和为1440°。
知识应用
解:设这个多边形的边数为n,
可列方程(n-2)×180°= 1080°.
解得n=8
答:这个多边形是八边形。
3、小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
4、已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是 。
144°
这节课学习了什么?
n边形的内角和等于(n-2).180°
A
B
C
D
A
B
C
D
O
证明思路:
多边形
三角形
转化
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,能求出n边形的内角和吗?请同学们课后试一试。
课后探究
谢 谢
