湘教版数学七年级下册 第3章 整式的乘法章末复习 课件(共28张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 第3章 整式的乘法章末复习 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 796.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 16:53:13 | ||
图片预览





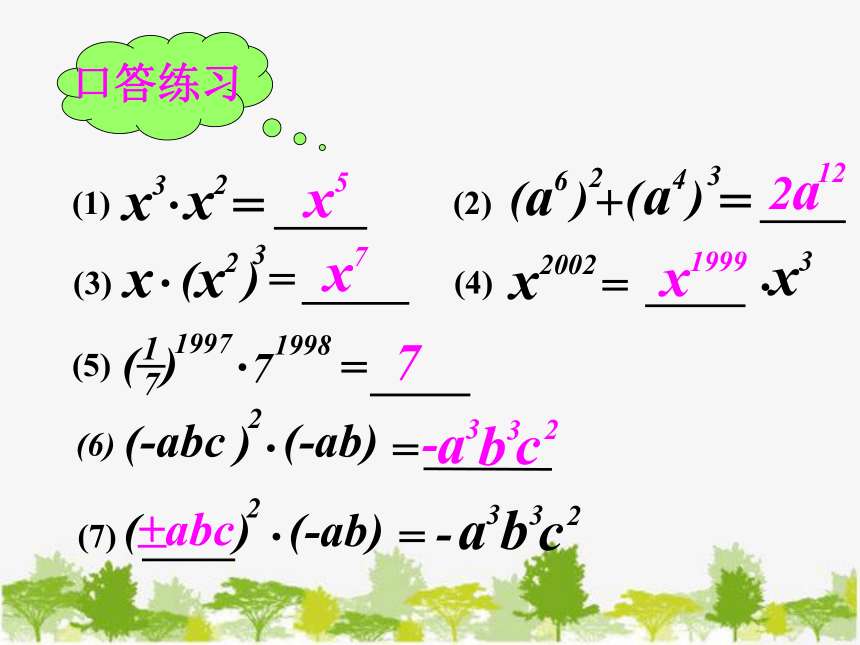


文档简介
(共28张PPT)
章末复习
湘教版 七年级下册
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
a
m
a
n
·
=
a
m+n
a
m
n
( )
=
a
mn
ab
n
( )
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3 )
=
[4 ( -3)]
a
3
a
2
( )
x
2
x
5
( )
b
=-12a
5
bx
7
复习导入
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
单项式与多项式相乘
多项式的乘法
a
m
a
n
·
=
a
m+n
a
m
( )
n
=
a
mn
ab
n
( )
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3 )
m(a+b)=
(a+b)(m+n)=
ma+mb
am+an+bm+bn
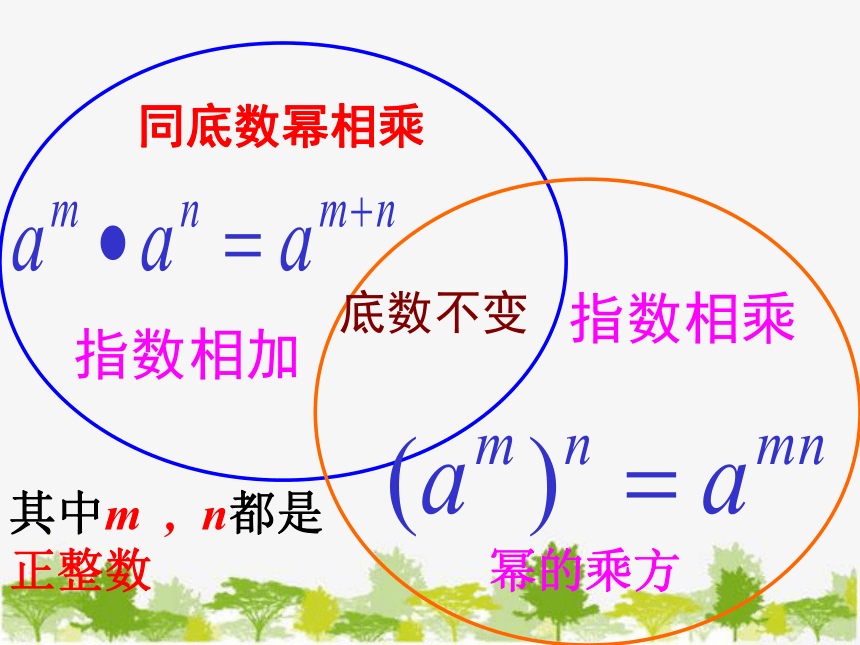
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
想
一
想
下列各题错在哪里?
a
2
a
3
a
5
+
=
(1)
a
2
a
a
2
·
=
(2)
(x-y)
2
(y-x)
5
=
(x-y)
7
(8)
x
2
( )
3
=
x
5
(4)
a
3
x
6
3
5
-(x-y)
7
(y-x)
7
·
·
4
7
(6)
(-5)
(-5)
=5
11
-5
11
(-3)
2
·
3
3
=
(-3)
5
(7)
2
(5)
3
5a
·
2a
=10a
6
10a
5
(3)
a
3
a
3
=2a
3
a
6
找一找
下列各式中运算正确的是( )
4
7
-
x
2
y
z
2
( )
7
4
-
x
y
2
( )
=
x
3
y
3
10
5
10
3
-
10
2
10
10
( )
( )
-2
·
·
3
( )
=
-6
2
1
-
6
1
-
a
2
b
3
a
8
b
27
( )
3
=
a
3n
2
3n
( )
·
b
2
( )
ab
( )
=
(A)
(D)
(B)
(C)
D
6n
复习巩固
口答练习
x
3
x
2
·
=
( )
a
6
2
+
a
4
3
( )
=
x
x
2
·
( )
3
=
x
3
x
2002
·
=
·
=
7
1
( )
1997
7
1998
2
=
·
( )
(-ab)
-
c
2
b
3
a
3
(1)
(3)
(7)
·
-abc
( )
(-ab)
2
=
(6)
(5)
(4)
(2)
x
5
2a
12
x
7
x
1999
7
-
a
3
b
3
c
2
+abc
比一比
算
计
(1)
3x
2
( )
3
-
7x
3
[ ]
x
3
-x
4x
2
+1
( )
a
2
( )
-2b
2
a+2b
( )
-2ab(a-b)
(2)
先化简,再求值:
其中
a=1,b=
2
1
.
公 式 的 反 向 使 用
公 式 的 反 向 使 用
试用简便方法计算:
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
(1) 23×53 ;
(2) (-5)16 × (-2)15
(3) 24 × 44 ×(-0.125)4 ;
= (2×5)3
= 103
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1
(1) (x5y) ÷ x2 = x5 2 ·y
(2) (8m2n2) ÷ (2m2n) = (8÷2 )·m2 2·n2 1 ;
(3) (a4b2c) ÷ (3a2b) = (1÷3 )·a4 2·b2 1·c .
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
写在商里面作
(被除式的指数) —(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂) 商的指数=
一个单项式;
?
因式。
单项式 的 除法 法则
如何进行单项式除以单项式的运算
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
观察 & 归纳
解: (2x y) ·(–7xy )÷(14x4y )
=-56x7y5 ÷(14x4y )
= -4x3y2
解:(2a+b)4÷(2a+b)
=(2a+b)
= 4a2+4ab+b2
=8x6y3 ·(–7xy )÷(14x4y )
= (2a+b)4-2
(1)(-a)8÷(-a2)
(2)-5a5b3c÷5a4b3
(4)-3a2x4y3÷(-axy2)
(5)(4×109)÷(-2×103)
口答
=-a6
=-ac
=3ax3y
=-2×106
(3) 6m2n÷(-2mn)
= -3m
你找到了 多项式除以单项式的规律 吗?
议一议
( a+b+c )÷m
=
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
例 题 解 析
例3 计算:
(2)原式=
=
(1)(-2a4b3c)3÷(-8a4b5c)
(3 )(-3.6×1010)÷(-2×102)2÷(3×102)2
小测
=a8b4c2
= –10
(2)(6x2y3)2÷(3xy2)2
=4x2y2
乘法公式
平方差公式
完全平方公式(两数和的平方)
(a+b)(a-b) =
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x +(a+b)x+ab
2
例1 计算 1998
2002
1998
2002 =
(2000-2)(2000+2)
=4000000-4
=3999996
解
想一想
下列计算是否正确?如不正确,应
如何改正?
(-x+6)(-x-6) =
-
x
2
-
6
(1)
2
-x
-
1
(-x-1)(x+1) =
(2)
=
(-x)
2
-
6
2
=
x
2
-
36
-(x+1)
=
(x+1)
=
-(x+1)
2
=
+
+
1
( )
x
2
2x
-
=
-
x
2
-
2x
-1
(3)
(-2xy-1)(2xy-1) =
1-2xy
2
=(-1)
2
-(2xy)
2
2
=1-4x
y
2
平方差公式的应用题:
1、利用分解因式简便计算
(1) 652-642 (2) 5.42-4.62
(3) (4)
解:652-642
=(65+64)(65-64)
=129×1
=129
解:5.42-4.62
=(5.4+4.6)(5.4-4.6)
=10×0.8
=8
答案:5
答案:28
提高题:
2、已知 , ,求(a+b)2-(a-b)2的值。
解: (a+b)2-(a-b)2
=[(a+b)+(a-b)][(a+b)-(a-b)]
=2a·2b
=4ab
当 , 时,
原式=4× ×
=
思考:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2+2ab+b2 =(a+b)2
a2-2ab+b2 = (a-b)2
什么关系?
完全平方公式
a2+2ab+b2 =(a+b)2
a2-2ab+b2 = (a-b)2
用他们可以把一个三项式分解因式的特点:
两项是两个数的平方
另一项是加上(或减去)这两个数积的两倍
x2-4x+4
=x2-4x+22
=(x-2)2
a2 +2a+1
= a2 +2·a·1 +12
=(a+1)2
a2+10a+25
=a2+2·a( ) +( )2
=(a+ )2
5
5
5
X2+12ax+36a2
=X2+2·x·6a +(6a)2
=(x+6a)2
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
章末复习
湘教版 七年级下册
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
a
m
a
n
·
=
a
m+n
a
m
n
( )
=
a
mn
ab
n
( )
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3 )
=
[4 ( -3)]
a
3
a
2
( )
x
2
x
5
( )
b
=-12a
5
bx
7
复习导入
整式的乘法
同底数幂的乘法
幂的乘方
积的乘方
单项式的乘法
单项式与多项式相乘
多项式的乘法
a
m
a
n
·
=
a
m+n
a
m
( )
n
=
a
mn
ab
n
( )
=
a
n
b
n
a
2
x
5
4
·
x
2
a
3
b
(-3 )
m(a+b)=
(a+b)(m+n)=
ma+mb
am+an+bm+bn
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
想
一
想
下列各题错在哪里?
a
2
a
3
a
5
+
=
(1)
a
2
a
a
2
·
=
(2)
(x-y)
2
(y-x)
5
=
(x-y)
7
(8)
x
2
( )
3
=
x
5
(4)
a
3
x
6
3
5
-(x-y)
7
(y-x)
7
·
·
4
7
(6)
(-5)
(-5)
=5
11
-5
11
(-3)
2
·
3
3
=
(-3)
5
(7)
2
(5)
3
5a
·
2a
=10a
6
10a
5
(3)
a
3
a
3
=2a
3
a
6
找一找
下列各式中运算正确的是( )
4
7
-
x
2
y
z
2
( )
7
4
-
x
y
2
( )
=
x
3
y
3
10
5
10
3
-
10
2
10
10
( )
( )
-2
·
·
3
( )
=
-6
2
1
-
6
1
-
a
2
b
3
a
8
b
27
( )
3
=
a
3n
2
3n
( )
·
b
2
( )
ab
( )
=
(A)
(D)
(B)
(C)
D
6n
复习巩固
口答练习
x
3
x
2
·
=
( )
a
6
2
+
a
4
3
( )
=
x
x
2
·
( )
3
=
x
3
x
2002
·
=
·
=
7
1
( )
1997
7
1998
2
=
·
( )
(-ab)
-
c
2
b
3
a
3
(1)
(3)
(7)
·
-abc
( )
(-ab)
2
=
(6)
(5)
(4)
(2)
x
5
2a
12
x
7
x
1999
7
-
a
3
b
3
c
2
+abc
比一比
算
计
(1)
3x
2
( )
3
-
7x
3
[ ]
x
3
-x
4x
2
+1
( )
a
2
( )
-2b
2
a+2b
( )
-2ab(a-b)
(2)
先化简,再求值:
其中
a=1,b=
2
1
.
公 式 的 反 向 使 用
公 式 的 反 向 使 用
试用简便方法计算:
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
(1) 23×53 ;
(2) (-5)16 × (-2)15
(3) 24 × 44 ×(-0.125)4 ;
= (2×5)3
= 103
= (-5)×[(-5)×(-2)]15
= -5×1015
= [2×4×(-0.125)]4
= 14
= 1
(1) (x5y) ÷ x2 = x5 2 ·y
(2) (8m2n2) ÷ (2m2n) = (8÷2 )·m2 2·n2 1 ;
(3) (a4b2c) ÷ (3a2b) = (1÷3 )·a4 2·b2 1·c .
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
写在商里面作
(被除式的指数) —(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂) 商的指数=
一个单项式;
?
因式。
单项式 的 除法 法则
如何进行单项式除以单项式的运算
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
观察 & 归纳
解: (2x y) ·(–7xy )÷(14x4y )
=-56x7y5 ÷(14x4y )
= -4x3y2
解:(2a+b)4÷(2a+b)
=(2a+b)
= 4a2+4ab+b2
=8x6y3 ·(–7xy )÷(14x4y )
= (2a+b)4-2
(1)(-a)8÷(-a2)
(2)-5a5b3c÷5a4b3
(4)-3a2x4y3÷(-axy2)
(5)(4×109)÷(-2×103)
口答
=-a6
=-ac
=3ax3y
=-2×106
(3) 6m2n÷(-2mn)
= -3m
你找到了 多项式除以单项式的规律 吗?
议一议
( a+b+c )÷m
=
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
例 题 解 析
例3 计算:
(2)原式=
=
(1)(-2a4b3c)3÷(-8a4b5c)
(3 )(-3.6×1010)÷(-2×102)2÷(3×102)2
小测
=a8b4c2
= –10
(2)(6x2y3)2÷(3xy2)2
=4x2y2
乘法公式
平方差公式
完全平方公式(两数和的平方)
(a+b)(a-b) =
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x +(a+b)x+ab
2
例1 计算 1998
2002
1998
2002 =
(2000-2)(2000+2)
=4000000-4
=3999996
解
想一想
下列计算是否正确?如不正确,应
如何改正?
(-x+6)(-x-6) =
-
x
2
-
6
(1)
2
-x
-
1
(-x-1)(x+1) =
(2)
=
(-x)
2
-
6
2
=
x
2
-
36
-(x+1)
=
(x+1)
=
-(x+1)
2
=
+
+
1
( )
x
2
2x
-
=
-
x
2
-
2x
-1
(3)
(-2xy-1)(2xy-1) =
1-2xy
2
=(-1)
2
-(2xy)
2
2
=1-4x
y
2
平方差公式的应用题:
1、利用分解因式简便计算
(1) 652-642 (2) 5.42-4.62
(3) (4)
解:652-642
=(65+64)(65-64)
=129×1
=129
解:5.42-4.62
=(5.4+4.6)(5.4-4.6)
=10×0.8
=8
答案:5
答案:28
提高题:
2、已知 , ,求(a+b)2-(a-b)2的值。
解: (a+b)2-(a-b)2
=[(a+b)+(a-b)][(a+b)-(a-b)]
=2a·2b
=4ab
当 , 时,
原式=4× ×
=
思考:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2+2ab+b2 =(a+b)2
a2-2ab+b2 = (a-b)2
什么关系?
完全平方公式
a2+2ab+b2 =(a+b)2
a2-2ab+b2 = (a-b)2
用他们可以把一个三项式分解因式的特点:
两项是两个数的平方
另一项是加上(或减去)这两个数积的两倍
x2-4x+4
=x2-4x+22
=(x-2)2
a2 +2a+1
= a2 +2·a·1 +12
=(a+1)2
a2+10a+25
=a2+2·a( ) +( )2
=(a+ )2
5
5
5
X2+12ax+36a2
=X2+2·x·6a +(6a)2
=(x+6a)2
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
