湘教版七年级下册6 数据的分析 课件(共13张PPT)
文档属性
| 名称 | 湘教版七年级下册6 数据的分析 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 209.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 16:21:47 | ||
图片预览





文档简介
(共13张PPT)
小结与复习
第6章 数据的分析
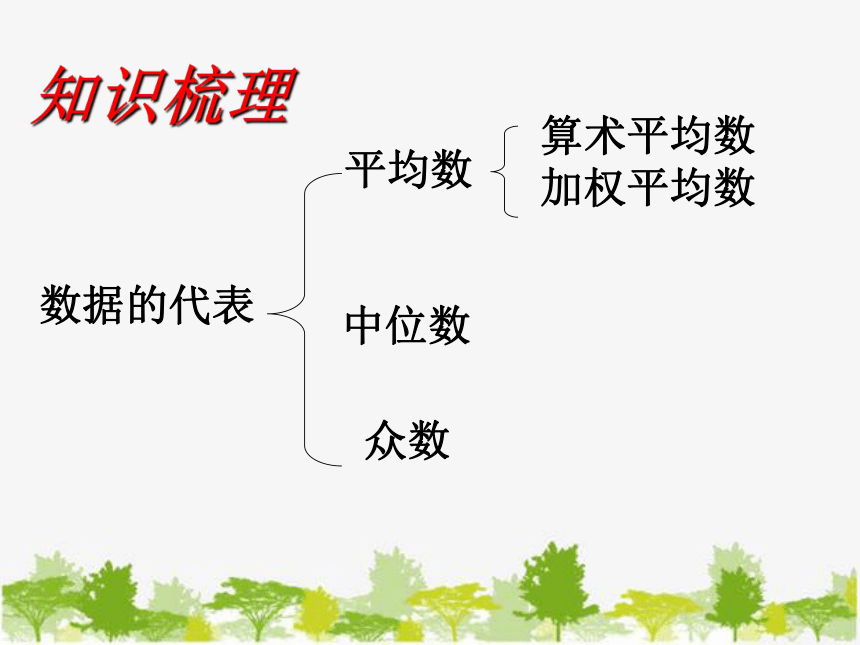
数据的代表
平均数
算术平均数
加权平均数
中位数
众数
知识梳理
问题1:求加权平均数的公式是什么?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数。
若n个数
的权分别是
则:
叫做这n个数的加权平均数。
将一组数据按照由小到大(或由大到小)的顺序排列如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
一组数据中出现次数最多的数据就是这组数据的众数。
★极差:一组数据中最大数据与最小数据的差。
极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大.
※各数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
方差越小,波动越小。方差越大,波动越大。
1、在一次英语口试中,10名学生的得分如下:80、70、90、100、80、60、80、70、90、100,则这次英语口试中,学生得分的众数是( )
2、八年级一班46个同学中,13岁的有5人,14岁的20人,15岁的有15人,16岁 的有6人。八年级一班学生年龄的平均分,中位数,众数分别是( )
3、有7个数由小到大依次排列,平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,这7个数的中位数是( )
随堂练习
4、设一组数据为a、b、c、d、a、c、d、d、a,其中a<b<c<d,则这组数据的中位数是( )
A、a B、b C、c、 D、d
5、已知一组数据x、-5、4、-3、2、-5;根据下列条件确定x的值;
(1)中位数为-1;
(2)平均数是3;
(3)x是唯一的众数;
6、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
预测项目 A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按4︰3︰1的比例确定各人的成绩,此时谁将录用?
(3)若要让最后的测试成绩从高到低为A、C、B,则权重可能是多少?
7、为了解某校八年级学生成长发肓情况,从全校八年级学生中随机抽取了100人测量体重,他们的体重频数分布表如下:
体重 45~49 50 ~54 55 ~59 60 ~64 65 ~69 70 ~74 75 ~79 80 ~84
频数 5 22 35 20 8 6 3 1
问:学校八年级学生的平均体重是多少?
8、 某次考试后,政治老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计
表。得分率=得该分数的人数/被统计的人数。
0
1
2
3
4
34.8%
10%
25.8%
9.8%
19.6%
分数 (分)
得分率
(1)老师估计该题能得2分或2分以上者,即可认为“比较好”,
在所统计的学生中共有224人不属于“比
较 好”。问统计的总人数为多少?
(2)求该题得分的众数、中位数
和平均数。
9、 数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数和众数分别为( )
学生数
答对题数
D
A 8,8 B 8,9 C 9,9 D 9,8
4
20
18
8
10、某中学要召开运动会,决定从九年级的150名女生中选30人,组成一个彩旗方队。现在抽测了10名女生的身高,结果如下(单位:厘米):166,154,151,167,162,158,158,160,162,162。
(1)依据样本数据估计该九年级全体女生的平均身高约是多少?
(2)这10名女生的身高的中位数、众数各是多少?
(3)请你依据样本数据,设计一个挑选参加方队的女生的方案。
小结与复习
第6章 数据的分析
数据的代表
平均数
算术平均数
加权平均数
中位数
众数
知识梳理
问题1:求加权平均数的公式是什么?
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数。
若n个数
的权分别是
则:
叫做这n个数的加权平均数。
将一组数据按照由小到大(或由大到小)的顺序排列如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
一组数据中出现次数最多的数据就是这组数据的众数。
★极差:一组数据中最大数据与最小数据的差。
极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大.
※各数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
方差越小,波动越小。方差越大,波动越大。
1、在一次英语口试中,10名学生的得分如下:80、70、90、100、80、60、80、70、90、100,则这次英语口试中,学生得分的众数是( )
2、八年级一班46个同学中,13岁的有5人,14岁的20人,15岁的有15人,16岁 的有6人。八年级一班学生年龄的平均分,中位数,众数分别是( )
3、有7个数由小到大依次排列,平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,这7个数的中位数是( )
随堂练习
4、设一组数据为a、b、c、d、a、c、d、d、a,其中a<b<c<d,则这组数据的中位数是( )
A、a B、b C、c、 D、d
5、已知一组数据x、-5、4、-3、2、-5;根据下列条件确定x的值;
(1)中位数为-1;
(2)平均数是3;
(3)x是唯一的众数;
6、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
预测项目 A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按4︰3︰1的比例确定各人的成绩,此时谁将录用?
(3)若要让最后的测试成绩从高到低为A、C、B,则权重可能是多少?
7、为了解某校八年级学生成长发肓情况,从全校八年级学生中随机抽取了100人测量体重,他们的体重频数分布表如下:
体重 45~49 50 ~54 55 ~59 60 ~64 65 ~69 70 ~74 75 ~79 80 ~84
频数 5 22 35 20 8 6 3 1
问:学校八年级学生的平均体重是多少?
8、 某次考试后,政治老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计
表。得分率=得该分数的人数/被统计的人数。
0
1
2
3
4
34.8%
10%
25.8%
9.8%
19.6%
分数 (分)
得分率
(1)老师估计该题能得2分或2分以上者,即可认为“比较好”,
在所统计的学生中共有224人不属于“比
较 好”。问统计的总人数为多少?
(2)求该题得分的众数、中位数
和平均数。
9、 数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数和众数分别为( )
学生数
答对题数
D
A 8,8 B 8,9 C 9,9 D 9,8
4
20
18
8
10、某中学要召开运动会,决定从九年级的150名女生中选30人,组成一个彩旗方队。现在抽测了10名女生的身高,结果如下(单位:厘米):166,154,151,167,162,158,158,160,162,162。
(1)依据样本数据估计该九年级全体女生的平均身高约是多少?
(2)这10名女生的身高的中位数、众数各是多少?
(3)请你依据样本数据,设计一个挑选参加方队的女生的方案。
