特殊的四边形—菱形 课件
图片预览






文档简介
课件24张PPT。特殊的平行四边形
-----菱形(1)
两组对边
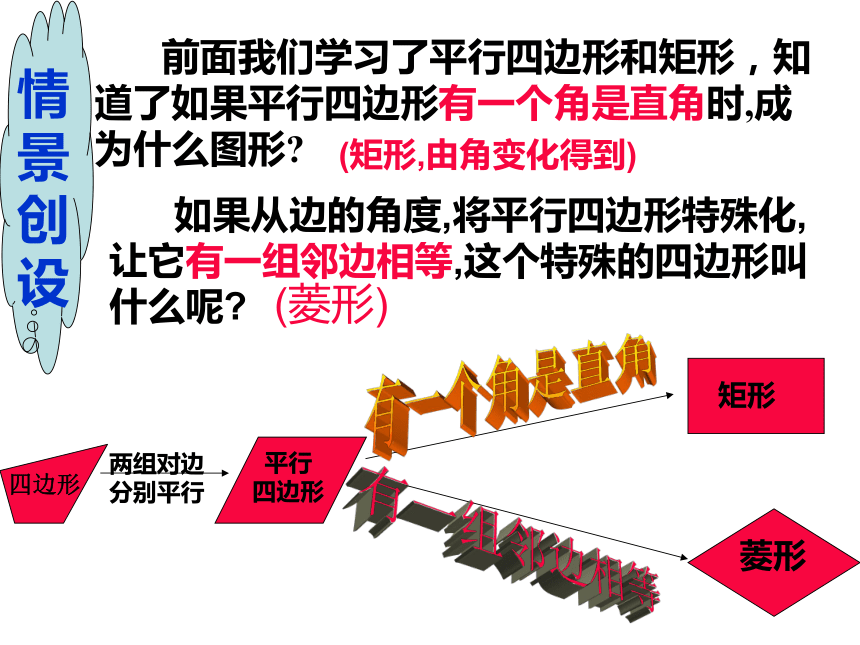
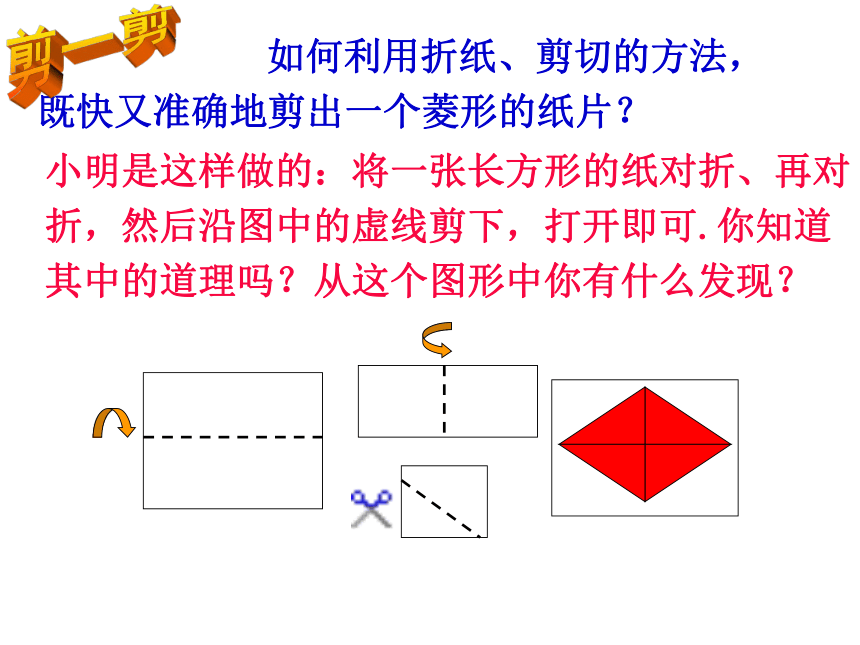
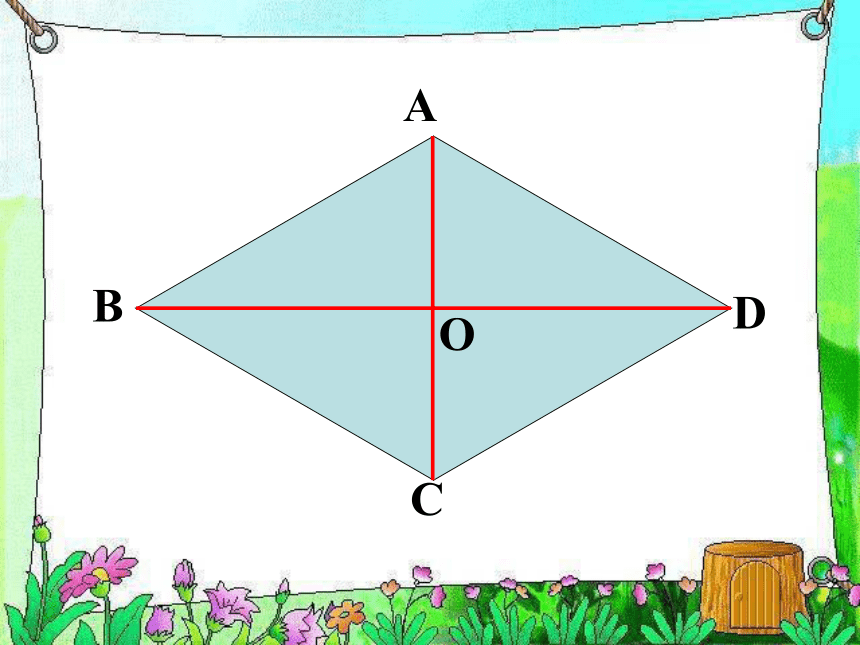
分别平行矩形 前面我们学习了平行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?有一个角是直角菱形有一组邻边相等(矩形,由角变化得到) 如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢?(菱形)四边形情景创设有一组邻边相等的平行四边形叫菱形. 平行四边形 邻边相等菱形在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?想一想如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?2000多年前…… 一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑生活感受菱形就在我们身边三菱汽车标志欣赏 小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?剪一剪ADOC B我们已经知道矩形和菱形是特殊的平行四边形,因此矩形菱形都是中心对称图形,想一想 矩形、菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?矩形是轴对称图形,对称轴有两条。菱形是轴对称图形,对称轴有两条。 由于平行四边形的对边相等,而菱形的邻边相等,因此我们得到:菱形的性质1:菱形的四条边都相等。菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质:菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.菱形的两条对角线互相垂直,每一条对角线平分一组对角。∵四边形ABCD是菱形∴ AD=AB,OD=OB∴ AC⊥BD∴∠9=∠10又∵ AO = AO∴△AOD ≌ △AOB∵ △AOD ≌ △AOB∴∠1=∠2
∴ AC平分∠DAB 同理:∠5=∠6 , ∠7=∠8
∴ BD平分∠ADC和∠ABC∴ ∠9=∠10= 90°已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC证明:菱形的性质2: O 6又∵ ∠9+∠10= 180°同理:∠3=∠4
∴ AC平分∠DCBO已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC证明2:∵四边形ABCD是菱形∴AB=AD,(菱形的定义) ∴ AC⊥BD ,AC平分∠DAB (为什么?)同理:AC平分∠DCB OD=OB (平行四边形的对角线互相平分) BD平分∠ADC和∠ABCDCBOA菱形的性质边角对角线对称性菱形的两组对边平行且相等几何语言∵四边形ABCD是菱形 菱形的四条边相等∴ AB=BC=CD=DA菱形的两组对角分别相等∴ ∠DAB=∠DCB
∠ADC=∠ABC 菱形的邻角互补∴ ∠DAB+∠ABC= 180° 菱形的两条对角线互相平分∴ OA=OC;OB=OD菱形的两条对角线互相垂直,
每一条对角线平分一组对角。∴ AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是中心对称图形,对称中心是两条对角线的交点。菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
1 24 3 5 76 8∵四边形ABCD是菱形,说说理由∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )OA=OC,OB=OD ( ) AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )你都掌握了吗?
练一练【菱形的面积公式】OES菱形=BC· AE思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗? 议一议 大显身手解:【菱形的面积公式】OES菱形=BC· AE思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗? 菱形面积:S菱形=底×高=对角线乘积的一半议一议 在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?试一试 =BD·AO+BD·CO =·BD· (AO+CO)=BD·AC =×10×18=90解:学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______。3cm60度3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm344、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)课堂小结1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想
-----菱形(1)
两组对边
分别平行矩形 前面我们学习了平行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?有一个角是直角菱形有一组邻边相等(矩形,由角变化得到) 如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢?(菱形)四边形情景创设有一组邻边相等的平行四边形叫菱形. 平行四边形 邻边相等菱形在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?想一想如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?2000多年前…… 一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗花纹——越王勾践剑生活感受菱形就在我们身边三菱汽车标志欣赏 小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?剪一剪ADOC B我们已经知道矩形和菱形是特殊的平行四边形,因此矩形菱形都是中心对称图形,想一想 矩形、菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?矩形是轴对称图形,对称轴有两条。菱形是轴对称图形,对称轴有两条。 由于平行四边形的对边相等,而菱形的邻边相等,因此我们得到:菱形的性质1:菱形的四条边都相等。菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质:菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.菱形的两条对角线互相垂直,每一条对角线平分一组对角。∵四边形ABCD是菱形∴ AD=AB,OD=OB∴ AC⊥BD∴∠9=∠10又∵ AO = AO∴△AOD ≌ △AOB∵ △AOD ≌ △AOB∴∠1=∠2
∴ AC平分∠DAB 同理:∠5=∠6 , ∠7=∠8
∴ BD平分∠ADC和∠ABC∴ ∠9=∠10= 90°已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC证明:菱形的性质2: O 6又∵ ∠9+∠10= 180°同理:∠3=∠4
∴ AC平分∠DCBO已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC证明2:∵四边形ABCD是菱形∴AB=AD,(菱形的定义) ∴ AC⊥BD ,AC平分∠DAB (为什么?)同理:AC平分∠DCB OD=OB (平行四边形的对角线互相平分) BD平分∠ADC和∠ABCDCBOA菱形的性质边角对角线对称性菱形的两组对边平行且相等几何语言∵四边形ABCD是菱形 菱形的四条边相等∴ AB=BC=CD=DA菱形的两组对角分别相等∴ ∠DAB=∠DCB
∠ADC=∠ABC 菱形的邻角互补∴ ∠DAB+∠ABC= 180° 菱形的两条对角线互相平分∴ OA=OC;OB=OD菱形的两条对角线互相垂直,
每一条对角线平分一组对角。∴ AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是中心对称图形,对称中心是两条对角线的交点。菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
1 24 3 5 76 8∵四边形ABCD是菱形,说说理由∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )OA=OC,OB=OD ( ) AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )你都掌握了吗?
练一练【菱形的面积公式】OES菱形=BC· AE思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗? 议一议 大显身手解:【菱形的面积公式】OES菱形=BC· AE思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗? 菱形面积:S菱形=底×高=对角线乘积的一半议一议 在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?试一试 =BD·AO+BD·CO =·BD· (AO+CO)=BD·AC =×10×18=90解:学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______。3cm60度3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm344、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)课堂小结1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想
