沪科版数学八年级下册 18.1 勾股定理教案(表格式)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览

文档简介
沪科版数学八年级下册18.1勾股定理 教学设计
课题 18.1勾股定理 单元 第18章第1节 学科 数学 年级 八年级下
学习 目标 【知识与技能】 1、探索直角三角形三边关系 2、了解勾股定理的发现过程 3、掌握勾股定理的内容,会用面积法证明勾股定理。 【过程与方法】 1、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。 2、在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的能力,并体会数形结合和特殊到一般的思想方法。 【情感态度与价值观】 1、介绍我国古代勾股定理研究方面所取得的成就,感受数学文化,激发学生的爱国热情,促其勤奋学习。 2、在探究活动中,培养学生的合作交流意识和探索精神。
重点 了解勾股定理的演绎过程,掌握勾股定理及其应用
难点 理解勾股定理的演绎和推导过程。
教学过程
教学环节 教师活动 学生活动 设计意图
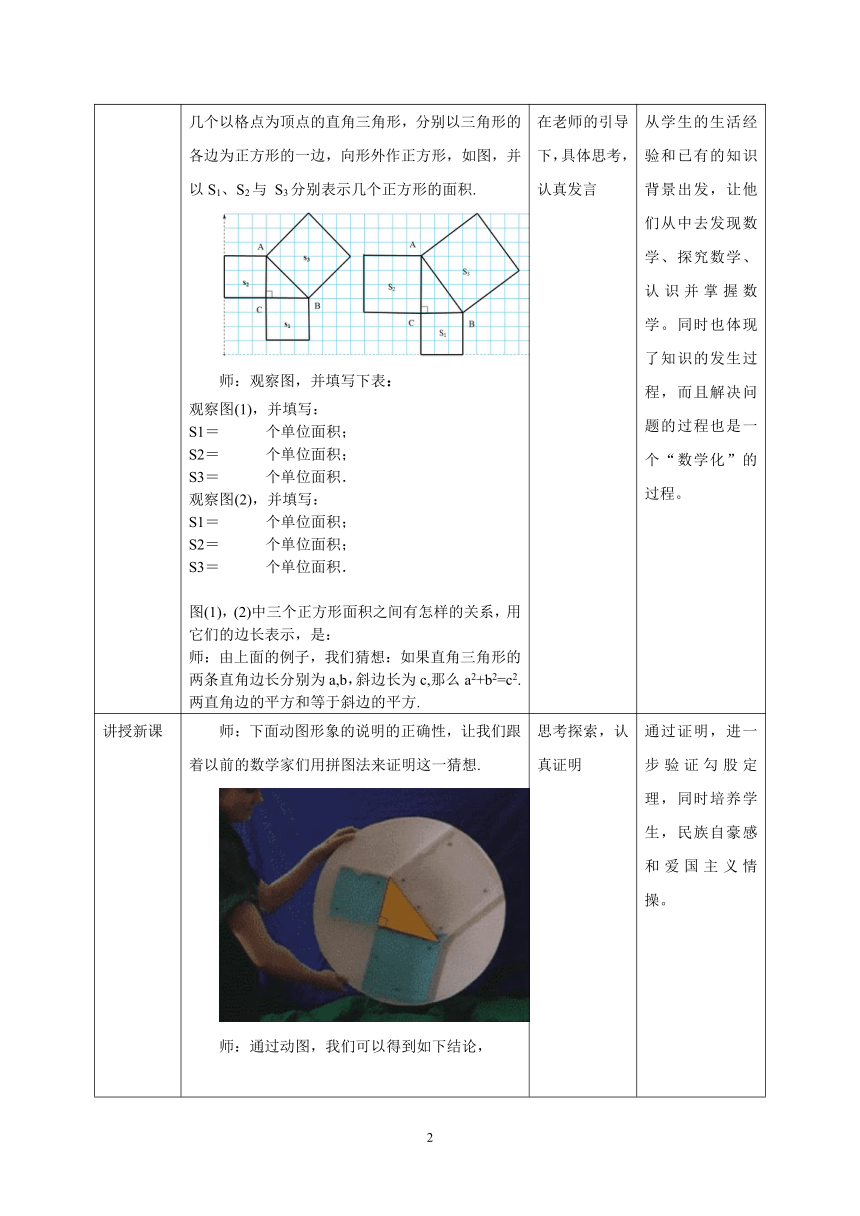
导入新课 播放有关勾股定理的电视剧片段 师: 我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图): 师:在行距、列距都是1的方格图中,任作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图,并以S1、S2与 S3分别表示几个正方形的面积. 师:观察图,并填写下表: 观察图(1),并填写: S1= 个单位面积; S2= 个单位面积; S3= 个单位面积. 观察图(2),并填写: S1= 个单位面积; S2= 个单位面积; S3= 个单位面积. 图(1),(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是: 师:由上面的例子,我们猜想:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方. 认真听讲积极思考 在老师的引导下,具体思考,认真发言 设置情景,调动学生的学习积极性,为新课学习做好铺垫。 从学生的生活经验和已有的知识背景出发,让他们从中去发现数学、探究数学、认识并掌握数学。同时也体现了知识的发生过程,而且解决问题的过程也是一个“数学化”的过程。
讲授新课 师:下面动图形象的说明的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想. 师:通过动图,我们可以得到如下结论, 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2 +b2 =c2.的平方和等于斜边的平方. 在外国则叫毕达哥拉斯定理,或百牛定理. 师:下面我们来看一下,我们的老祖先,赵爽是怎么证明的?下面这个图,叫做赵爽弦图。 证明:∵S大正方形=c2, S小正方形=(b-a)2, ∴S大正方形=4·S三角形+S小正方形, 观看视频了解美国总统证法。 思考探索,认真证明 通过证明,进一步验证勾股定理,同时培养学生,民族自豪感和爱国主义情操。
课堂练习 师:他们勾股定理都有什么用呢?下面我们来通过几个练习来看看它的应用。 1、求下列字母所代表的正方形的面积。 求出下列直角三角形中未知边的长度: 积极思考,完成练习 通过练习,进一步巩固,勾股定理,掌握并运用其解决一些实际问题。
课堂小结 谈谈你的收获和体会吧! ⒈是不是所有的三角形三边关系都满足勾股定理? ⒉在发现勾股定理的过程中,我们用了什么方法? ⒊据不完全统计,勾股定理的证明方法已经多达400多种,今天我们用了什么方法? 4.运用勾股定理应注意哪些事项? (1)前提条件是在直角三角形中; (2)弄清哪个角是直角; 认真回顾梳理知识,积极回答问题 引导学生回忆本节知识,梳理本节内容,使知识内化。
课题 18.1勾股定理 单元 第18章第1节 学科 数学 年级 八年级下
学习 目标 【知识与技能】 1、探索直角三角形三边关系 2、了解勾股定理的发现过程 3、掌握勾股定理的内容,会用面积法证明勾股定理。 【过程与方法】 1、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。 2、在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验证”的能力,并体会数形结合和特殊到一般的思想方法。 【情感态度与价值观】 1、介绍我国古代勾股定理研究方面所取得的成就,感受数学文化,激发学生的爱国热情,促其勤奋学习。 2、在探究活动中,培养学生的合作交流意识和探索精神。
重点 了解勾股定理的演绎过程,掌握勾股定理及其应用
难点 理解勾股定理的演绎和推导过程。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 播放有关勾股定理的电视剧片段 师: 我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图): 师:在行距、列距都是1的方格图中,任作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图,并以S1、S2与 S3分别表示几个正方形的面积. 师:观察图,并填写下表: 观察图(1),并填写: S1= 个单位面积; S2= 个单位面积; S3= 个单位面积. 观察图(2),并填写: S1= 个单位面积; S2= 个单位面积; S3= 个单位面积. 图(1),(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是: 师:由上面的例子,我们猜想:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方. 认真听讲积极思考 在老师的引导下,具体思考,认真发言 设置情景,调动学生的学习积极性,为新课学习做好铺垫。 从学生的生活经验和已有的知识背景出发,让他们从中去发现数学、探究数学、认识并掌握数学。同时也体现了知识的发生过程,而且解决问题的过程也是一个“数学化”的过程。
讲授新课 师:下面动图形象的说明的正确性,让我们跟着以前的数学家们用拼图法来证明这一猜想. 师:通过动图,我们可以得到如下结论, 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2 +b2 =c2.的平方和等于斜边的平方. 在外国则叫毕达哥拉斯定理,或百牛定理. 师:下面我们来看一下,我们的老祖先,赵爽是怎么证明的?下面这个图,叫做赵爽弦图。 证明:∵S大正方形=c2, S小正方形=(b-a)2, ∴S大正方形=4·S三角形+S小正方形, 观看视频了解美国总统证法。 思考探索,认真证明 通过证明,进一步验证勾股定理,同时培养学生,民族自豪感和爱国主义情操。
课堂练习 师:他们勾股定理都有什么用呢?下面我们来通过几个练习来看看它的应用。 1、求下列字母所代表的正方形的面积。 求出下列直角三角形中未知边的长度: 积极思考,完成练习 通过练习,进一步巩固,勾股定理,掌握并运用其解决一些实际问题。
课堂小结 谈谈你的收获和体会吧! ⒈是不是所有的三角形三边关系都满足勾股定理? ⒉在发现勾股定理的过程中,我们用了什么方法? ⒊据不完全统计,勾股定理的证明方法已经多达400多种,今天我们用了什么方法? 4.运用勾股定理应注意哪些事项? (1)前提条件是在直角三角形中; (2)弄清哪个角是直角; 认真回顾梳理知识,积极回答问题 引导学生回忆本节知识,梳理本节内容,使知识内化。
