人教版八年级下册 18.2.1矩形 课件(共21张PPT)
文档属性
| 名称 | 人教版八年级下册 18.2.1矩形 课件(共21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 448.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 20:09:57 | ||
图片预览






文档简介
(共21张PPT)
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经研究了平行四边形,下面我们通过平行四边形角、边的特殊化,研究特殊的平行四边形—— 矩形。
18.2 特殊的平行四边形
18.2.1 矩形
第一课时
一、学习目标:
1.理解矩形的概念,明确矩形与平行四 边形的区别与联系。
2.探索并证明矩形的性质,会用矩形性质解决相关问题。
3.理解“直角三角形斜边上的中线等于斜边上的一半”这一重要结论。
学习重点:
1.矩形的性质。
2.直角三角形斜边上的中线的性质。
二、自学指导
阅读教材52-53页的内容后回答下列问题。时间:10分钟。
1.矩形的定义?
2.矩形的性质?矩形具备而平行四边形不具备的性质?
3.直角三角形斜边上的中线的性质?
三、学生小组交流,探究新知
四、质疑答疑学生遇到难点,教师适当点拨
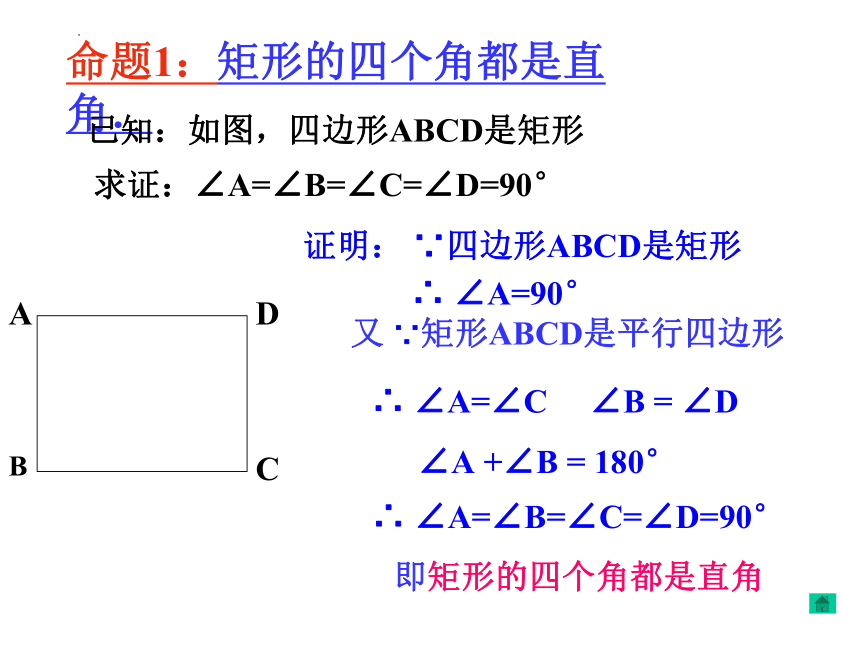
有一个角是直角的平行四边形
1.矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
也叫长方形
是矩形
2.矩形的性质的研究
三、矩形 两条对角线互相平分
二、矩形的两组对角分别相等
一、矩形的两组对边分别平行且相等
四、矩形的邻角互补
小组讨论:矩形是否具备其他特殊的性质呢?
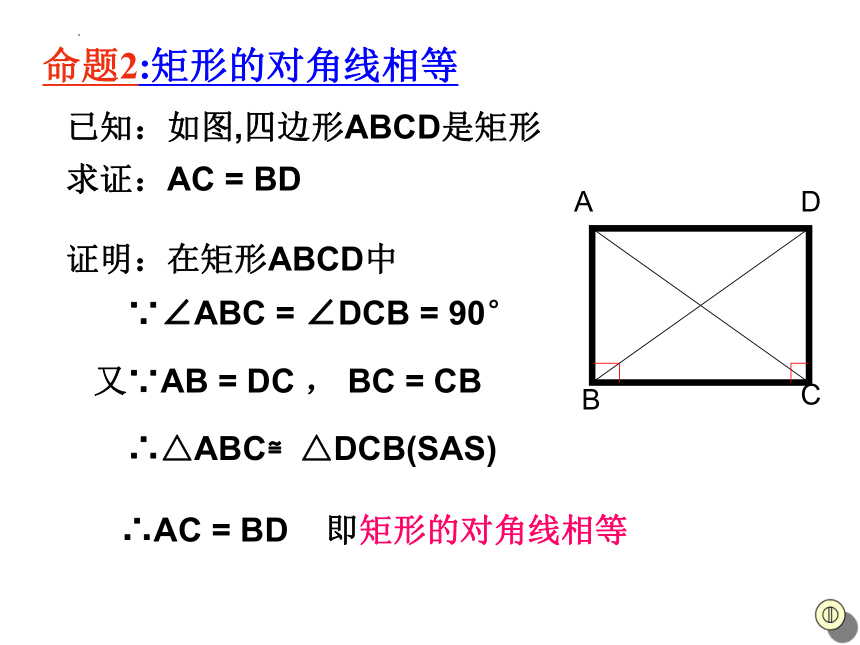
命题1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 ∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD 即矩形的对角线相等
命题2:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
你能用数学语言描述吗?
A
B
C
D
O
归纳:矩形的性质
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
3.研究直角三角形斜边上的中线的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
练习1
五、课堂检测
1、矩形具有而平行四边形不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8.5 (D)6.5
B
D
D
从一般到特殊
边
角
对角线
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
2.直角三角形斜边上的中线性质
1.矩形的定义:
有一个角是直角的平行四边形叫做矩形
六、课堂小结
2.矩形的性质:
七、课后作业
4.已知:如图,四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB= _______ ㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
谢谢!
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
复习巩固
我是平行四边形,我的角,边,对角线都有哪些特性呢
A D
B C
O
边 角 对角线 对称性
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
对边平行
且相等
两组对边
分别平行
平行
四边形
矩形
情景创设
我们已经研究了平行四边形,下面我们通过平行四边形角、边的特殊化,研究特殊的平行四边形—— 矩形。
18.2 特殊的平行四边形
18.2.1 矩形
第一课时
一、学习目标:
1.理解矩形的概念,明确矩形与平行四 边形的区别与联系。
2.探索并证明矩形的性质,会用矩形性质解决相关问题。
3.理解“直角三角形斜边上的中线等于斜边上的一半”这一重要结论。
学习重点:
1.矩形的性质。
2.直角三角形斜边上的中线的性质。
二、自学指导
阅读教材52-53页的内容后回答下列问题。时间:10分钟。
1.矩形的定义?
2.矩形的性质?矩形具备而平行四边形不具备的性质?
3.直角三角形斜边上的中线的性质?
三、学生小组交流,探究新知
四、质疑答疑学生遇到难点,教师适当点拨
有一个角是直角的平行四边形
1.矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
也叫长方形
是矩形
2.矩形的性质的研究
三、矩形 两条对角线互相平分
二、矩形的两组对角分别相等
一、矩形的两组对边分别平行且相等
四、矩形的邻角互补
小组讨论:矩形是否具备其他特殊的性质呢?
命题1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 ∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD 即矩形的对角线相等
命题2:矩形的对角线相等
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
你能用数学语言描述吗?
A
B
C
D
O
归纳:矩形的性质
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
3.研究直角三角形斜边上的中线的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
练习1
五、课堂检测
1、矩形具有而平行四边形不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8.5 (D)6.5
B
D
D
从一般到特殊
边
角
对角线
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
2.直角三角形斜边上的中线性质
1.矩形的定义:
有一个角是直角的平行四边形叫做矩形
六、课堂小结
2.矩形的性质:
七、课后作业
4.已知:如图,四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB= _______ ㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
谢谢!
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
复习巩固
我是平行四边形,我的角,边,对角线都有哪些特性呢
A D
B C
O
边 角 对角线 对称性
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
对边平行
且相等
