人教版八年级下册18.2.3正方形课件(共22张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.3正方形课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
正方形
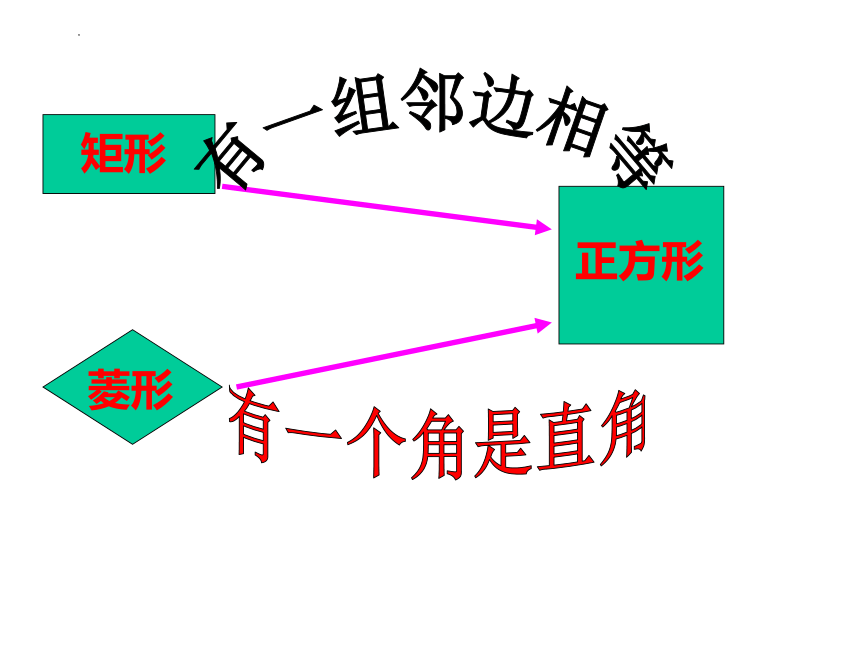
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
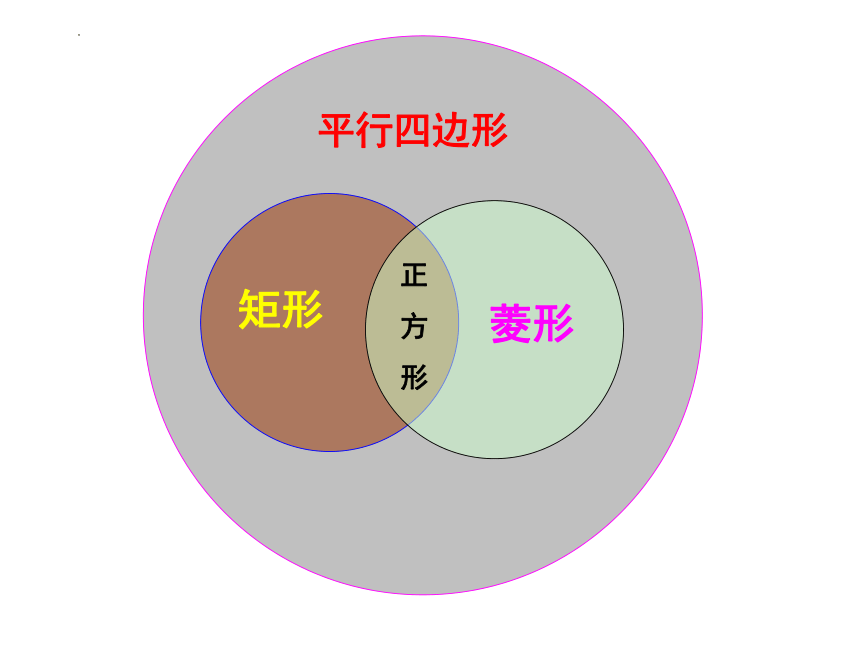
平行四边形
矩形
菱形
正
方
形
讨论:正方形有哪些性质和判定方法?
1.对角线互相垂直且相等的平行四边形是正方形?
2.对角线互相垂直的矩形是正方形?
3.对角线相等的菱形是正方形?
4.对角线互相垂直平分且相等的四边形是正方形?
思考?
活动
1.从长方形木板中怎样截出最大的正方形木板
2.怎样使菱形的衣帽架变成正方形的衣帽架
3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验
一下方巾是否是正方形的。
1.要使一个菱形成为正方形需
增加的条件是_______.
(填上一个条件即可)
做一做
2、要使一个矩形成为正方形需添加的条件是________.
(填上一个条件即可)
3.下列正确的是
A. 四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是 正方形
D.对角线互相垂直平分且相等的 四边形是正方形
4.已知:正方形ABCD对角线AC、BD相交于点O,且AB=2cm,则AC的长是_____,正方形的面积是 ____。
5.已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6 cm,则正方形的面积是______, 周长是______.
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
例2.点E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN,试判断四边形EFMN是什么图形?并证明你的结论。
A
B
C
D
N
E
F
M
练一练:
请打开书101页做练习1,2
通过今天的学习你有哪些收获?
课堂检测 点E、F、M、N分别是正方形ABCD四条边上的中点,试判断四边形EFMN是什么图形?并证明你的结论。
A
B
C
D
N
E
F
M
巩固提高
如图,正方形ABCD中,AC、BD相交于O, MN∥BC且MN分别交OB、OA于M、N, 求证:CM=DN。
A
B
C
D
M
N
O
例.已知:在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M. 试判断点F在CD的延长线上移动时,∠MFD的大小是否变化?若变化,请求出变化范围;若不变化,请求出其度数.
B
C
D
F
E
A
M
练习:
1.如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。
求证:∠CEA=∠ABG
D
B
C
A
F
G
E
A
B
C
P
D
E
3.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
求证:① PE=PD ; ② PE⊥PD;
小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”。他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论。你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由。
中考全接触
A
A
A
A
B
B
B
B
C
C
C
C
D
D
E
D
D
E
E
E
F
F
F
F
图①
图②
图③
图④
如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
测试
正方形
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
平行四边形
矩形
菱形
正
方
形
讨论:正方形有哪些性质和判定方法?
1.对角线互相垂直且相等的平行四边形是正方形?
2.对角线互相垂直的矩形是正方形?
3.对角线相等的菱形是正方形?
4.对角线互相垂直平分且相等的四边形是正方形?
思考?
活动
1.从长方形木板中怎样截出最大的正方形木板
2.怎样使菱形的衣帽架变成正方形的衣帽架
3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验
一下方巾是否是正方形的。
1.要使一个菱形成为正方形需
增加的条件是_______.
(填上一个条件即可)
做一做
2、要使一个矩形成为正方形需添加的条件是________.
(填上一个条件即可)
3.下列正确的是
A. 四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是 正方形
D.对角线互相垂直平分且相等的 四边形是正方形
4.已知:正方形ABCD对角线AC、BD相交于点O,且AB=2cm,则AC的长是_____,正方形的面积是 ____。
5.已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6 cm,则正方形的面积是______, 周长是______.
例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
例2.点E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN,试判断四边形EFMN是什么图形?并证明你的结论。
A
B
C
D
N
E
F
M
练一练:
请打开书101页做练习1,2
通过今天的学习你有哪些收获?
课堂检测 点E、F、M、N分别是正方形ABCD四条边上的中点,试判断四边形EFMN是什么图形?并证明你的结论。
A
B
C
D
N
E
F
M
巩固提高
如图,正方形ABCD中,AC、BD相交于O, MN∥BC且MN分别交OB、OA于M、N, 求证:CM=DN。
A
B
C
D
M
N
O
例.已知:在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M. 试判断点F在CD的延长线上移动时,∠MFD的大小是否变化?若变化,请求出变化范围;若不变化,请求出其度数.
B
C
D
F
E
A
M
练习:
1.如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。
求证:∠CEA=∠ABG
D
B
C
A
F
G
E
A
B
C
P
D
E
3.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
求证:① PE=PD ; ② PE⊥PD;
小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”。他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论。你同意小明的观点吗?若同意,请结合图④加以证明;若不同意,请说明理由。
中考全接触
A
A
A
A
B
B
B
B
C
C
C
C
D
D
E
D
D
E
E
E
F
F
F
F
图①
图②
图③
图④
如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
测试
