第18章平行四边形小专题复习(三)课件-人教版八年级数学下册(共16张PPT)
文档属性
| 名称 | 第18章平行四边形小专题复习(三)课件-人教版八年级数学下册(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 262.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
《平行四边形》小专题复习(三)
1、了解两个全等三角形拼平行四边形的方法,体会分类思想.
2、在平行四边形背景下,能用勾股定理建立方程求线段长.
学习目标
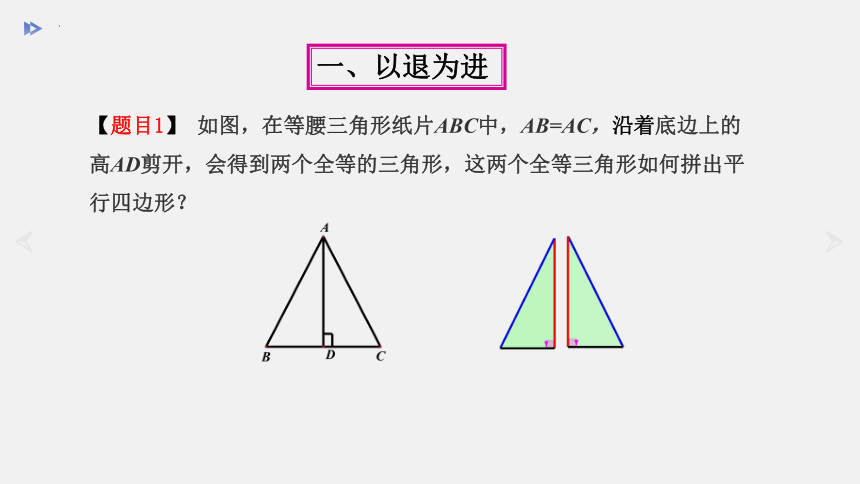
【题目1】 如图,在等腰三角形纸片ABC中,AB=AC,沿着底边上的高AD剪开,会得到两个全等的三角形,这两个全等三角形如何拼出平行四边形?
一、以退为进
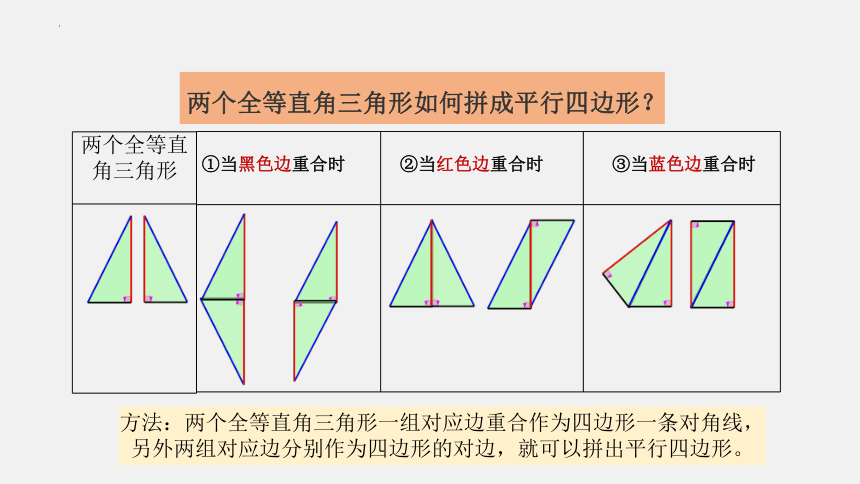
方法:两个全等直角三角形一组对应边重合作为四边形一条对角线,另外两组对应边分别作为四边形的对边,就可以拼出平行四边形。
两个全等直角三角形
两个全等直角三角形如何拼成平行四边形?
①当黑色边重合时
②当红色边重合时
③当蓝色边重合时
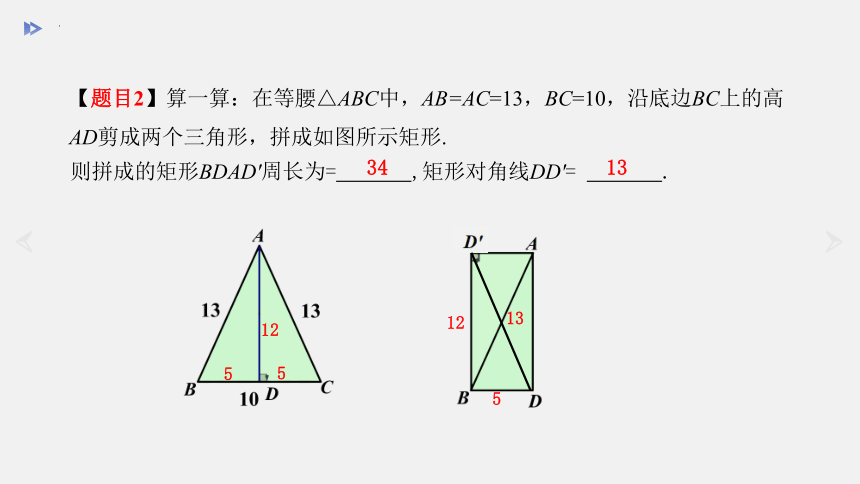
【题目2】算一算:在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,拼成如图所示矩形.
则拼成的矩形BDAD'周长为= ,矩形对角线DD'= .
5
5
12
34
13
5
12
13
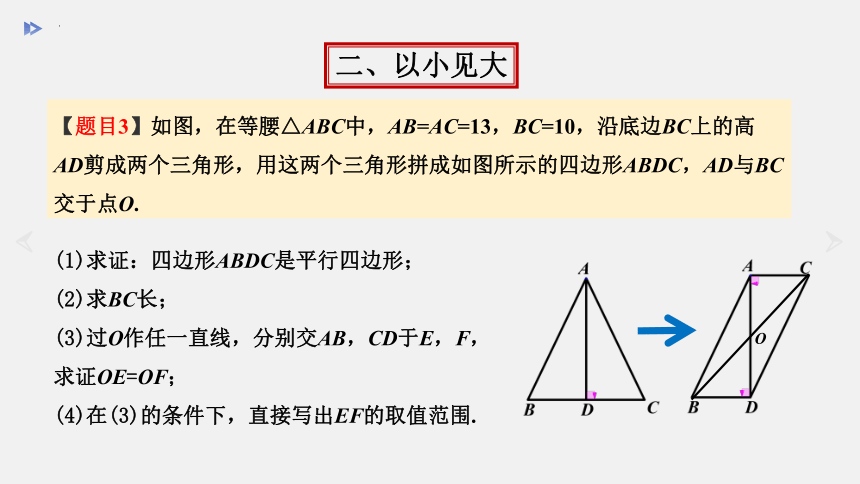
【题目3】如图,在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成如图所示的四边形ABDC,AD与BC交于点O.
二、以小见大
(1)求证:四边形ABDC是平行四边形;
(2)求BC长;
(3)过O作任一直线,分别交AB,CD于E,F, 求证OE=OF;
(4)在(3)的条件下,直接写出EF的取值范围.
O
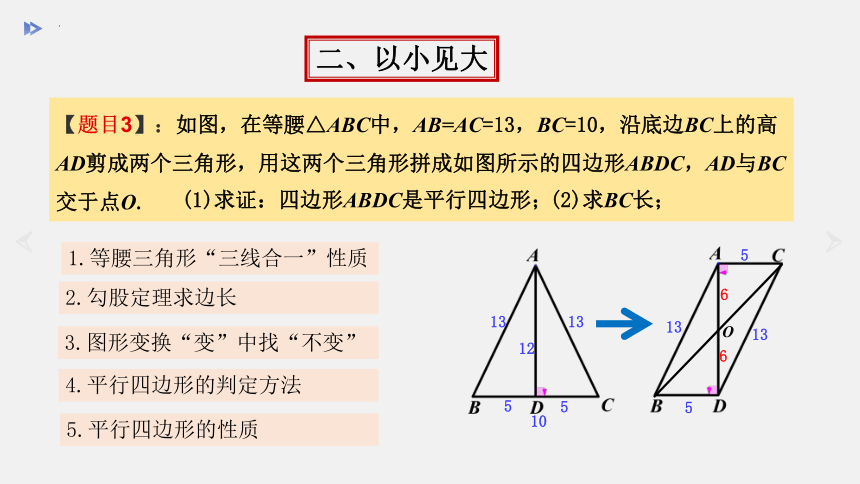
【题目3】:如图,在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成如图所示的四边形ABDC,AD与BC交于点O.
二、以小见大
5.平行四边形的性质
12
5
5
13
13
5
5
13
13
1.等腰三角形“三线合一”性质
2.勾股定理求边长
3.图形变换“变”中找“不变”
4.平行四边形的判定方法
10
6
6
(2)求BC长;
(1)求证:四边形ABDC是平行四边形;
O
13
13
解题过程
10
5
13
13
5
在四边形ABDC中,
AB=CD=13,BD=AC=5,
∴四边形ABDC是平行四边形.
5
5
12
13
?
?
解法二:
延长BD,过点C作CE⊥BD交于点E,
O
O
5
5
13
13
(3)过O作任一直线,分别交AB,CD于点E,F,求证OE=OF;
(4)在(3)的条件下,直接写出EF的取值范围.
(3)解:如图,过点O作直线EF,
分别交AB,CD于点E和F,
∴∠AEO=∠DFO,∠EAO=∠FDO,
∴OE=OF.
E
F
E
F
【题目4】(课本P62第14题)如图,在等腰三角形纸片ABC中,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,求平行四边形的对角线的长.
解:分类画出符合条件的平行四边形:
三、学以致用
(1)当AB边为对角线时,
(2)当AD边为对角线时,
(3)当BD边为对角线时,
h
h
n
(3)解:当BD边为对角线时,如图所示.
连接AG,延长GB,
过点A作BG的垂线AH,垂足为H,
∵∠ADB=∠DBH=∠H=90°,
∴四边形AHBD是矩形,
∴HB=AD=h,AH=DB=n,
GH=HB+BG=h+h=2h,
在Rt△AHG中,
?
?
.
图1
图2
图3
四、课堂小结
如图,在等腰直角三角形纸片ABC中,∠BAC=90°,AB=AC,BC=8,沿底边上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,请求出平行四边形对角线的长.
五、课后作业
《平行四边形》小专题复习(三)
1、了解两个全等三角形拼平行四边形的方法,体会分类思想.
2、在平行四边形背景下,能用勾股定理建立方程求线段长.
学习目标
【题目1】 如图,在等腰三角形纸片ABC中,AB=AC,沿着底边上的高AD剪开,会得到两个全等的三角形,这两个全等三角形如何拼出平行四边形?
一、以退为进
方法:两个全等直角三角形一组对应边重合作为四边形一条对角线,另外两组对应边分别作为四边形的对边,就可以拼出平行四边形。
两个全等直角三角形
两个全等直角三角形如何拼成平行四边形?
①当黑色边重合时
②当红色边重合时
③当蓝色边重合时
【题目2】算一算:在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,拼成如图所示矩形.
则拼成的矩形BDAD'周长为= ,矩形对角线DD'= .
5
5
12
34
13
5
12
13
【题目3】如图,在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成如图所示的四边形ABDC,AD与BC交于点O.
二、以小见大
(1)求证:四边形ABDC是平行四边形;
(2)求BC长;
(3)过O作任一直线,分别交AB,CD于E,F, 求证OE=OF;
(4)在(3)的条件下,直接写出EF的取值范围.
O
【题目3】:如图,在等腰△ABC中,AB=AC=13,BC=10,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成如图所示的四边形ABDC,AD与BC交于点O.
二、以小见大
5.平行四边形的性质
12
5
5
13
13
5
5
13
13
1.等腰三角形“三线合一”性质
2.勾股定理求边长
3.图形变换“变”中找“不变”
4.平行四边形的判定方法
10
6
6
(2)求BC长;
(1)求证:四边形ABDC是平行四边形;
O
13
13
解题过程
10
5
13
13
5
在四边形ABDC中,
AB=CD=13,BD=AC=5,
∴四边形ABDC是平行四边形.
5
5
12
13
?
?
解法二:
延长BD,过点C作CE⊥BD交于点E,
O
O
5
5
13
13
(3)过O作任一直线,分别交AB,CD于点E,F,求证OE=OF;
(4)在(3)的条件下,直接写出EF的取值范围.
(3)解:如图,过点O作直线EF,
分别交AB,CD于点E和F,
∴∠AEO=∠DFO,∠EAO=∠FDO,
∴OE=OF.
E
F
E
F
【题目4】(课本P62第14题)如图,在等腰三角形纸片ABC中,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,求平行四边形的对角线的长.
解:分类画出符合条件的平行四边形:
三、学以致用
(1)当AB边为对角线时,
(2)当AD边为对角线时,
(3)当BD边为对角线时,
h
h
n
(3)解:当BD边为对角线时,如图所示.
连接AG,延长GB,
过点A作BG的垂线AH,垂足为H,
∵∠ADB=∠DBH=∠H=90°,
∴四边形AHBD是矩形,
∴HB=AD=h,AH=DB=n,
GH=HB+BG=h+h=2h,
在Rt△AHG中,
?
?
.
图1
图2
图3
四、课堂小结
如图,在等腰直角三角形纸片ABC中,∠BAC=90°,AB=AC,BC=8,沿底边上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,请求出平行四边形对角线的长.
五、课后作业
