人教版八年级数学下册 第18章平行四边形小专题复习(四)课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第18章平行四边形小专题复习(四)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
平行四边形 小专题复习(四)
学 习 目 标
1.会综合运用基本图形的性质和判定进行计算和证明;
2.掌握证明一条线段等于两条线段和差的方法, 体会图形之间相互转化解决问题的联系.
以退为进
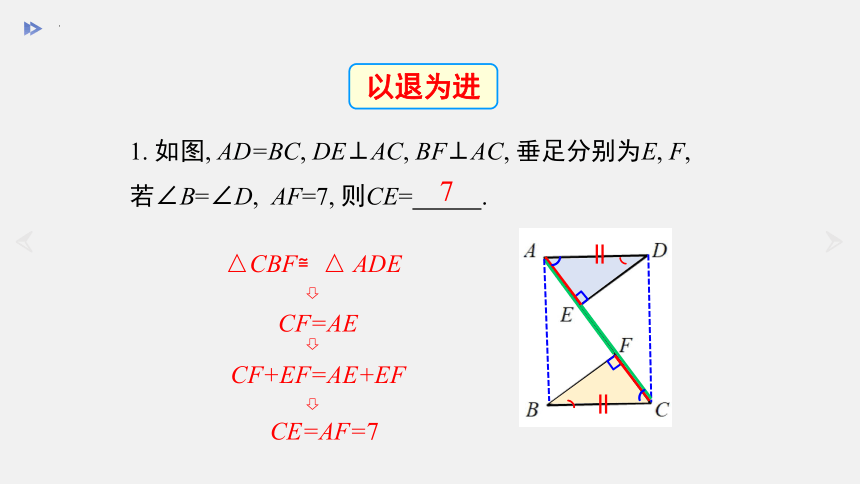
1. 如图, AD=BC, DE⊥AC, BF⊥AC, 垂足分别为E, F,
若∠B=∠D, AF=7, 则CE= .
7
△CBF≌△ ADE
=
=
CF=AE
CF+EF=AE+EF
CE=AF=7
以退为进
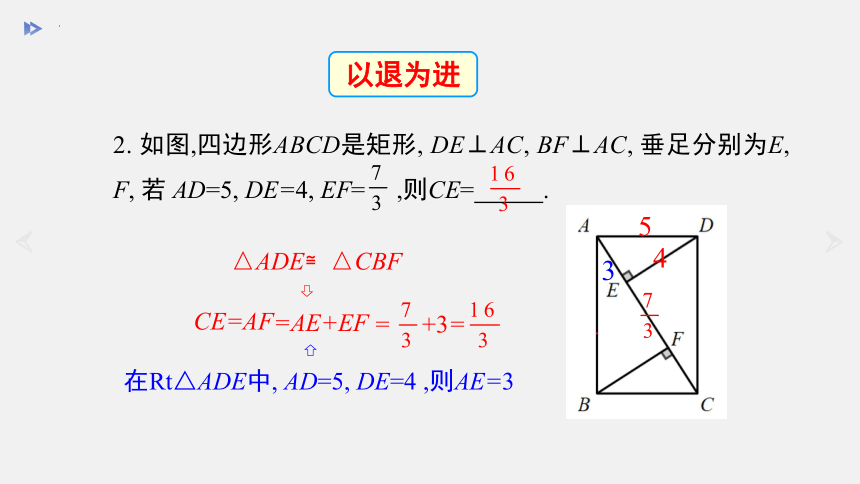
2. 如图,四边形ABCD是矩形, DE⊥AC, BF⊥AC, 垂足分别为E, F, 若 AD=5, DE=4, EF= ,则CE= .
△ADE≌△CBF
CE=AF
在Rt△ADE中, AD=5, DE=4 ,则AE=3
=AE+EF
4
5
3
= +3=
E
以退为进
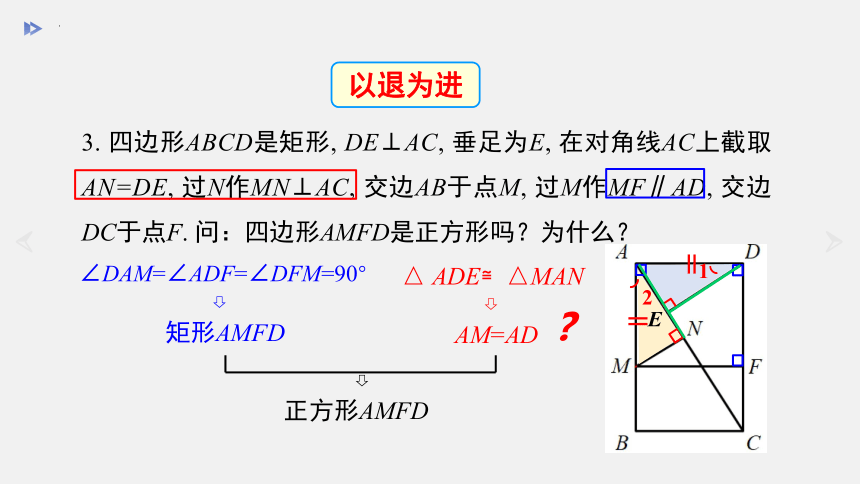
3. 四边形ABCD是矩形, DE⊥AC, 垂足为E, 在对角线AC上截取AN=DE, 过N作MN⊥AC, 交边AB于点M, 过M作MF∥AD, 交边DC于点F. 问:四边形AMFD是正方形吗?为什么?
∠DAM=∠ADF=∠DFM=90°
矩形AMFD
△ ADE≌△MAN
正方形AMFD
1
2
=
=
AM=AD
以小见大
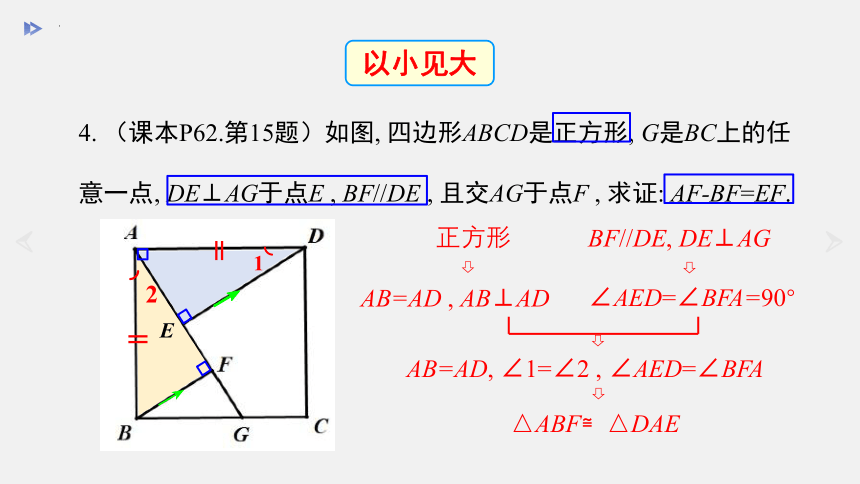
△ABF≌△DAE
=
=
正方形
AB=AD , AB⊥AD
BF//DE, DE⊥AG
∠AED=∠BFA=90°
AB=AD, ∠1=∠2 , ∠AED=∠BFA
1
2
←
←
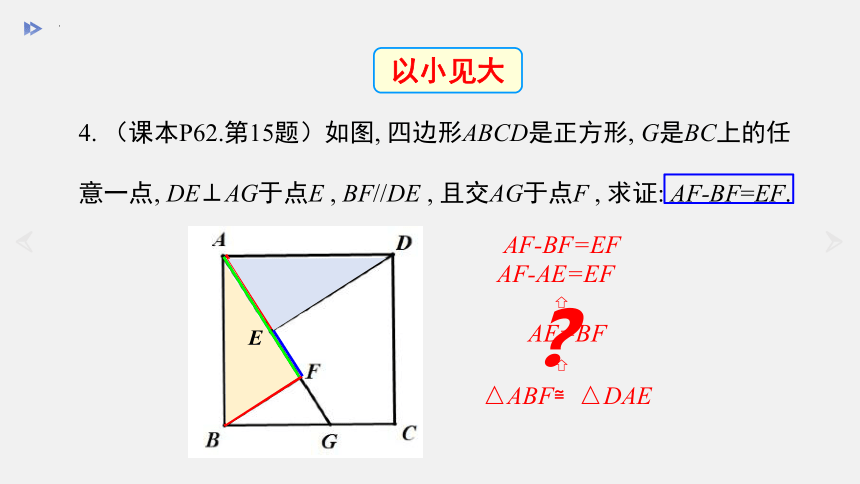
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
E
以小见大
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
△ABF≌△DAE
AF-BF=EF
AE=BF
AF-AE=EF
E
以小见大
=
=
∟
1
2
证明:
∵DE⊥AG,
∴∠AED =90°.
∵BF//DE,
∴∠AFB=∠AED =90°.
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
∵四边形ABCD是正方形,
∴∠DAB =90°, AB =AD,
∴∠1+∠DAE=∠2+∠DAE=90°.
∴∠1=∠2.
∴BF=AE.
∴AF-BF=AF-AE=EF.
∴△ABF≌△DAE.
全等 + 等量代换
线段和差.
小拓展
若“G是BC上的任意一点”改为“G是直线BC上的任意一点”, 则线段AF, BF, EF存在什么数量关系?
点G的位置有几种情况?
①点G在线段BC的反向延长线上时,
BF + AF=EF.
②点G在线段BC延长线上时,
BF-AF=EF.
BF
AF
EF
F
=
=
1
2
小拓展
若“G是BC上的任意一点”改为“G是直线BC上的任意一点”, 则线段AF, BF, EF存在什么数量关系?
②BF+AF=EF
③BF-AF=EF
①AF-BF =EF
如图, 直线MN过正方形ABCD的顶点A, 过点B, D分别作直线MN的垂线交于点F, E,当直线MN绕点A 转动时, △ABF与△DAE始终全等.
小结论
正方形 等腰直角三角形
H
I
学以致用
5.如图, 四边形ABCD是正方形, DE⊥AE于点E, CI⊥DE于点I, 过B作BF//DE, 交AE的延长线于点F, 交CI于点H, 求证:AE+EI=CI.
证明: 在正方形ABCD中, ∠ADC=90°, AD =CD ,
∵ CI⊥DE,
∴∠ADC=∠AED=∠CID =90°.
∴∠ADE+∠CDI=∠DCI+ ∠CDI.
∴∠ADE =∠DCI.
∴△ADE≌△DCI.
∴AE=DI, DE=CI.
∵DI+EI=DE,
∴AE+EI=CI .
△ABF≌△DAE ≌△CDI ≌△BCH
∵DI+EI=DE
↓
∴AE+EI=CI
↓
课堂小结
→
→
→
→
三角形 四边形
全等 + 等量代换 线段和差
课后作业
课本P62.第13题:
如图, E, F, M, N分别是正方形ABCD四条边上的点, 且AE=BF=CM=DN, 试判断四边形EFMN是什么图形, 并证明你的结论.
平行四边形 小专题复习(四)
学 习 目 标
1.会综合运用基本图形的性质和判定进行计算和证明;
2.掌握证明一条线段等于两条线段和差的方法, 体会图形之间相互转化解决问题的联系.
以退为进
1. 如图, AD=BC, DE⊥AC, BF⊥AC, 垂足分别为E, F,
若∠B=∠D, AF=7, 则CE= .
7
△CBF≌△ ADE
=
=
CF=AE
CF+EF=AE+EF
CE=AF=7
以退为进
2. 如图,四边形ABCD是矩形, DE⊥AC, BF⊥AC, 垂足分别为E, F, 若 AD=5, DE=4, EF= ,则CE= .
△ADE≌△CBF
CE=AF
在Rt△ADE中, AD=5, DE=4 ,则AE=3
=AE+EF
4
5
3
= +3=
E
以退为进
3. 四边形ABCD是矩形, DE⊥AC, 垂足为E, 在对角线AC上截取AN=DE, 过N作MN⊥AC, 交边AB于点M, 过M作MF∥AD, 交边DC于点F. 问:四边形AMFD是正方形吗?为什么?
∠DAM=∠ADF=∠DFM=90°
矩形AMFD
△ ADE≌△MAN
正方形AMFD
1
2
=
=
AM=AD
以小见大
△ABF≌△DAE
=
=
正方形
AB=AD , AB⊥AD
BF//DE, DE⊥AG
∠AED=∠BFA=90°
AB=AD, ∠1=∠2 , ∠AED=∠BFA
1
2
←
←
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
E
以小见大
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
△ABF≌△DAE
AF-BF=EF
AE=BF
AF-AE=EF
E
以小见大
=
=
∟
1
2
证明:
∵DE⊥AG,
∴∠AED =90°.
∵BF//DE,
∴∠AFB=∠AED =90°.
4. (课本P62.第15题)如图, 四边形ABCD是正方形, G是BC上的任意一点, DE⊥AG于点E , BF//DE , 且交AG于点F , 求证: AF-BF=EF.
∵四边形ABCD是正方形,
∴∠DAB =90°, AB =AD,
∴∠1+∠DAE=∠2+∠DAE=90°.
∴∠1=∠2.
∴BF=AE.
∴AF-BF=AF-AE=EF.
∴△ABF≌△DAE.
全等 + 等量代换
线段和差.
小拓展
若“G是BC上的任意一点”改为“G是直线BC上的任意一点”, 则线段AF, BF, EF存在什么数量关系?
点G的位置有几种情况?
①点G在线段BC的反向延长线上时,
BF + AF=EF.
②点G在线段BC延长线上时,
BF-AF=EF.
BF
AF
EF
F
=
=
1
2
小拓展
若“G是BC上的任意一点”改为“G是直线BC上的任意一点”, 则线段AF, BF, EF存在什么数量关系?
②BF+AF=EF
③BF-AF=EF
①AF-BF =EF
如图, 直线MN过正方形ABCD的顶点A, 过点B, D分别作直线MN的垂线交于点F, E,当直线MN绕点A 转动时, △ABF与△DAE始终全等.
小结论
正方形 等腰直角三角形
H
I
学以致用
5.如图, 四边形ABCD是正方形, DE⊥AE于点E, CI⊥DE于点I, 过B作BF//DE, 交AE的延长线于点F, 交CI于点H, 求证:AE+EI=CI.
证明: 在正方形ABCD中, ∠ADC=90°, AD =CD ,
∵ CI⊥DE,
∴∠ADC=∠AED=∠CID =90°.
∴∠ADE+∠CDI=∠DCI+ ∠CDI.
∴∠ADE =∠DCI.
∴△ADE≌△DCI.
∴AE=DI, DE=CI.
∵DI+EI=DE,
∴AE+EI=CI .
△ABF≌△DAE ≌△CDI ≌△BCH
∵DI+EI=DE
↓
∴AE+EI=CI
↓
课堂小结
→
→
→
→
三角形 四边形
全等 + 等量代换 线段和差
课后作业
课本P62.第13题:
如图, E, F, M, N分别是正方形ABCD四条边上的点, 且AE=BF=CM=DN, 试判断四边形EFMN是什么图形, 并证明你的结论.
