人教版八年级数学下册 第18章平行四边形小专题复习(五)课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第18章平行四边形小专题复习(五)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
《平行四边形》小专题复习(五)
学习目标
1.能运用正方形和全等三角形的性质与判定方法进行证明;
2.会在运动变化中发现不变的位置关系与数量关系。
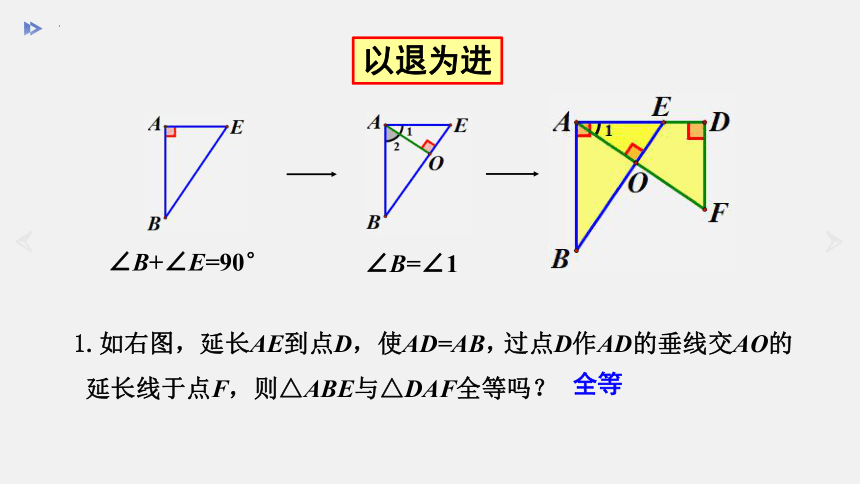
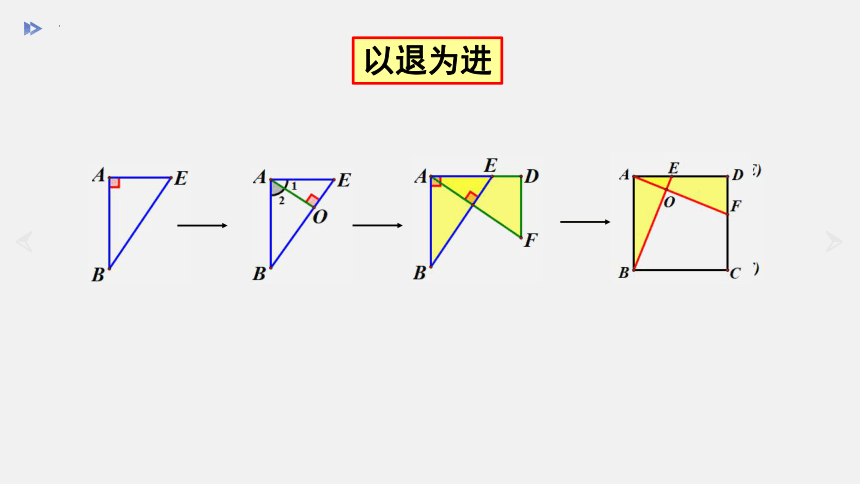
以退为进
∠B+∠E=90°
∠B=∠1
1.如右图,延长AE到点D,使AD=AB,
过点D作AD的垂线交AO的延长线于点F,则△ABE与△DAF全等吗?
全等
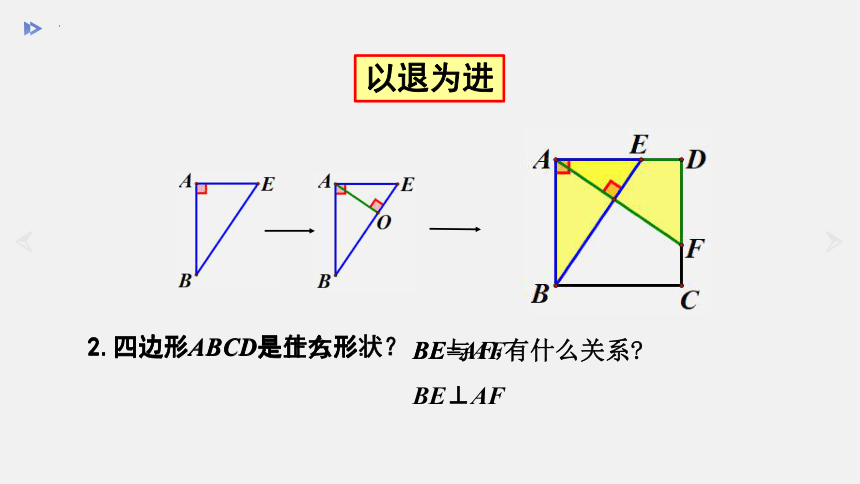
以退为进
2.四边形ABCD是什么形状?
2.四边形ABCD是正方形.
BE与AF有什么关系
BE=AF, BE⊥AF
以退为进
以小见大
例题 如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF. 要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
BE=AF
O
BE⊥AF
(课本第68页第8题)
1
3
.
AE=DF.
△ ABE≌△DAF,
AD-DE=CD-CF,
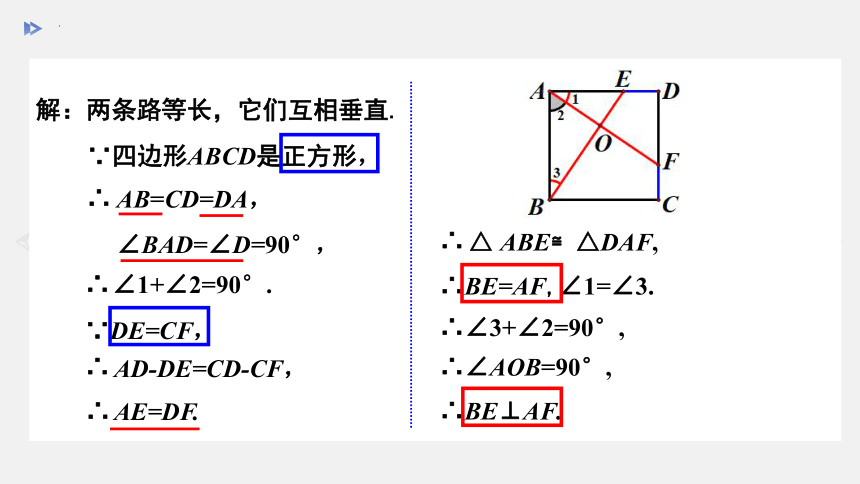
解:两条路等长,它们互相垂直.
∴
∴
∴∠AOB=90°,
∴∠3+∠2=90°,
∴
∵四边形ABCD是正方形,
AB=CD=DA,
∠BAD=∠D=90°,
∠1+∠2=90°.
∴
∵DE=CF,
∴
∴BE=AF,∠1=∠3.
∴BE⊥AF.
变式1 如图,正方形花园ABCD中修建两条路BE和AF,
且满足BE⊥AF,这两条路等长吗?DE=CF 吗?
BE=AF,
△ ABE≌△DAF
AE=DF
变式2 如图,若在正方形ABCD花园的AB边上再增加一个门(点G),若
修建小路BE,GF,发现BE⊥GF,问BE与GF有什么数量关系?为什么?
BE=GF
△ ABE≌△MFG
M
1
2
1
2
构造全等三角形
作平行线
作垂线
平移
学以致用
如图,在正方形ABCD花园的四边各开一个门,分别用点E,F , H ,G表示,修建小路EH,GF,发现EH⊥GF,问EH与GF有什么数量关系?为什么?
EH=GF
全等
M
N
平移
学以致用
变式 如图,在正方形ABCD花园的四边各开一个门,分别用点E,F , H , G表示,修建小路EH,GF,发现EH=GF,问EH⊥GF吗?为什么?
K
EH与GF不一定垂直
P
归纳总结
DE=CF
DE=CF
(图1)
(图2)
(图3)
归纳总结
正方形ABCD中,EH⊥GF,
当DE=CF时,
四边形EFHG一定是正方形.
作业布置
如图,点E,H,F,G分别在正方形ABCD的各边上,连接EF,GH,若EF⊥GH,则
(1)若EF=4,求GH的长;
(2)连接EH,HF,FG,GE,DE=CH,
求证:四边形EHFG是正方形.
《平行四边形》小专题复习(五)
学习目标
1.能运用正方形和全等三角形的性质与判定方法进行证明;
2.会在运动变化中发现不变的位置关系与数量关系。
以退为进
∠B+∠E=90°
∠B=∠1
1.如右图,延长AE到点D,使AD=AB,
过点D作AD的垂线交AO的延长线于点F,则△ABE与△DAF全等吗?
全等
以退为进
2.四边形ABCD是什么形状?
2.四边形ABCD是正方形.
BE与AF有什么关系
BE=AF, BE⊥AF
以退为进
以小见大
例题 如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF. 要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
BE=AF
O
BE⊥AF
(课本第68页第8题)
1
3
.
AE=DF.
△ ABE≌△DAF,
AD-DE=CD-CF,
解:两条路等长,它们互相垂直.
∴
∴
∴∠AOB=90°,
∴∠3+∠2=90°,
∴
∵四边形ABCD是正方形,
AB=CD=DA,
∠BAD=∠D=90°,
∠1+∠2=90°.
∴
∵DE=CF,
∴
∴BE=AF,∠1=∠3.
∴BE⊥AF.
变式1 如图,正方形花园ABCD中修建两条路BE和AF,
且满足BE⊥AF,这两条路等长吗?DE=CF 吗?
BE=AF,
△ ABE≌△DAF
AE=DF
变式2 如图,若在正方形ABCD花园的AB边上再增加一个门(点G),若
修建小路BE,GF,发现BE⊥GF,问BE与GF有什么数量关系?为什么?
BE=GF
△ ABE≌△MFG
M
1
2
1
2
构造全等三角形
作平行线
作垂线
平移
学以致用
如图,在正方形ABCD花园的四边各开一个门,分别用点E,F , H ,G表示,修建小路EH,GF,发现EH⊥GF,问EH与GF有什么数量关系?为什么?
EH=GF
全等
M
N
平移
学以致用
变式 如图,在正方形ABCD花园的四边各开一个门,分别用点E,F , H , G表示,修建小路EH,GF,发现EH=GF,问EH⊥GF吗?为什么?
K
EH与GF不一定垂直
P
归纳总结
DE=CF
DE=CF
(图1)
(图2)
(图3)
归纳总结
正方形ABCD中,EH⊥GF,
当DE=CF时,
四边形EFHG一定是正方形.
作业布置
如图,点E,H,F,G分别在正方形ABCD的各边上,连接EF,GH,若EF⊥GH,则
(1)若EF=4,求GH的长;
(2)连接EH,HF,FG,GE,DE=CH,
求证:四边形EHFG是正方形.
