人教版八年级数学下册 第20章数据的分析 小结课件(共17张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第20章数据的分析 小结课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
《数据的分析》小结
会求加权平均数、众数、中位数,能选择适当的统计量表示数据的集中趋势;
会计算方差,会表示数据的离散程度;
了解统计学的发展.
学 习 目 标
我校将举办数学实验技能比赛. 赛制要求:
1. 参加对象:全体初二年级同学;
2. 比赛内容:个人笔试、小组实验操作测试.
全班同学,分成五个小组,组织了一次班级模拟比赛,并随机选了两个小组13名同学的比赛成绩,进行分析.
班里两个小组参赛的笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87.
乙组:84 100 41 100 97 88.
一、收集数据
平均数
众数
中位数
方差
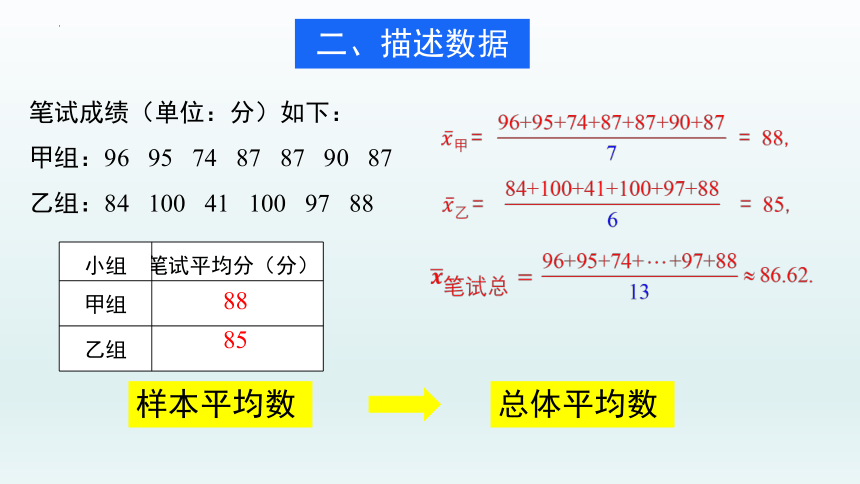
二、描述数据
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
小组 笔试平均分(分)
甲组
乙组
88
85
样本平均数
总体平均数
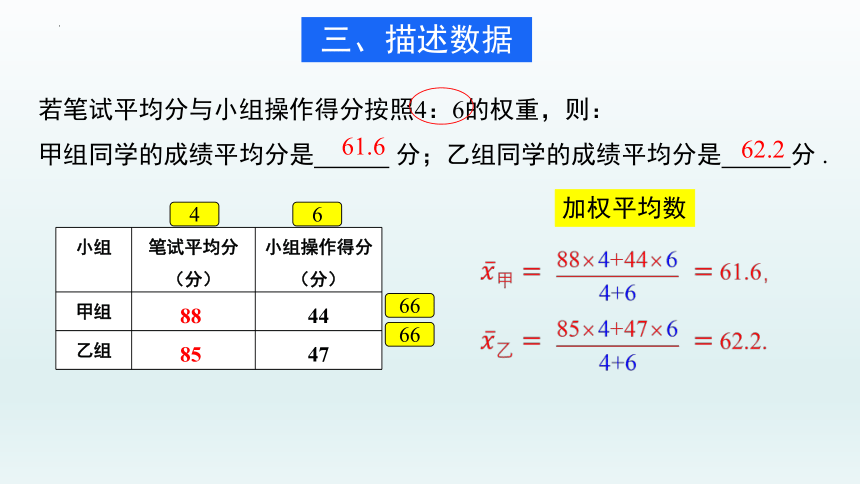
若笔试平均分与小组操作得分按照4:6的权重,则:
甲组同学的成绩平均分是 分;乙组同学的成绩平均分是 分 .
61.6
62.2
4
6
三、描述数据
小组 笔试平均分 (分) 小组操作得分
(分)
甲组 88 44
乙组 85 47
加权平均数
66
66
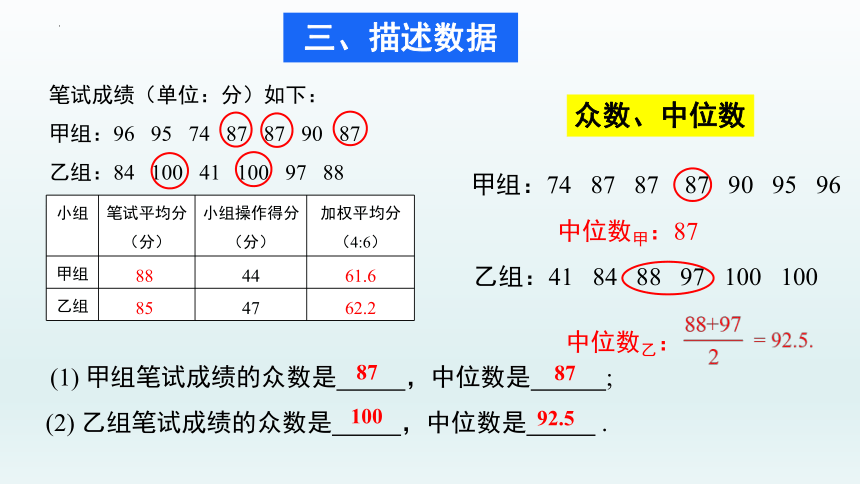
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
(1) 甲组笔试成绩的众数是 ,中位数是 ;
(2) 乙组笔试成绩的众数是 ,中位数是 .
87
100
中位数乙:
甲组:74 87 87 87 90 95 96
乙组:41 84 88 97 100 100
87
92.5
三、描述数据
小组 笔试平均分 (分) 小组操作得分 (分) 加权平均分
(4:6)
甲组 88 44 61.6
乙组 85 47 62.2
众数、中位数
中位数甲:87
组的笔试成绩稳定性高.
甲
小组 笔试平均分(分) 小组操作 得分(分) 加权平均分 (4:6) 众数 中位数
甲组 88 44 61.6 87 87
乙组 85 47 62.2 100 92.5
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
三、描述数据
组的笔试成绩稳定性高.
甲
< ,
方 差
三、描述数据
小组 笔试平均分(分) 小组操作 得分(分) 加权平均分 (4:6) 众数 中位数
甲组 88 44 61.6 87 87
乙组 85 47 62.2 100 92.5
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
甲组 笔试平均分 88
中位数 87
众数 87
方差 45.14
乙组 笔试平均分 85
中位数 92.5
众数 100
方差 423.33
估计在88分左右
稳
估计在92分左右
不稳定
√
四、分析数据
小组 笔试平均分 (分) 小组操作得分 (分) 加权平均分
(4:6)
甲组 88 44 61.6
乙组 85 47 62.2
平均数
数据的分析
数据的集中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
用样本平均数估计总体平均数
用样本方差估计总体方差
小结
《根据死亡公告的自然和政治的观察》
统计学的发展
古 往
格朗特 (J. Graunt , 1620 -1674) .
整理数据
用数学揭示数字之间的关系
发现新的真相
提取数据信息
统计学的发展
古 往
高斯 (C. F.Gass , 1777 -1855) .
勒让德 (A. -M.Legendre , 1752 -1833) .
关于最小二乘法的工作
皮尔逊 (K. Pearson , 1857 -1936) .
总体
根据样本对总体进行推断
对数据的推断
费希尔 (R.A. Fisher , 1890 -1962) .
试验设计分支及相应的方差分析方法等
统计学的发展
今 来
克拉默 (H. Cramer , 1893 -1985) .
1946年《统计学的数学方法》
数
据
初中的统计学
收集数据
整理数据
描述数据
分析数据
1. 举例说明平均数、中位数、众数的意义;
2. 算术平均数和加权平均数有什么联系和区别?举例说明加权平均数中“权”的意义;
3. 举例说明怎样用方差刻画数据的波动程度;
4. 举例说明刻画数据特征的量在决策中的作用;
5. 你认为统计学在生活中有什么意义和价值?
学后反思
课本
P136 复习巩固 第1题
P137 综合运用 第6题
课后作业
《数据的分析》小结
会求加权平均数、众数、中位数,能选择适当的统计量表示数据的集中趋势;
会计算方差,会表示数据的离散程度;
了解统计学的发展.
学 习 目 标
我校将举办数学实验技能比赛. 赛制要求:
1. 参加对象:全体初二年级同学;
2. 比赛内容:个人笔试、小组实验操作测试.
全班同学,分成五个小组,组织了一次班级模拟比赛,并随机选了两个小组13名同学的比赛成绩,进行分析.
班里两个小组参赛的笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87.
乙组:84 100 41 100 97 88.
一、收集数据
平均数
众数
中位数
方差
二、描述数据
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
小组 笔试平均分(分)
甲组
乙组
88
85
样本平均数
总体平均数
若笔试平均分与小组操作得分按照4:6的权重,则:
甲组同学的成绩平均分是 分;乙组同学的成绩平均分是 分 .
61.6
62.2
4
6
三、描述数据
小组 笔试平均分 (分) 小组操作得分
(分)
甲组 88 44
乙组 85 47
加权平均数
66
66
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
(1) 甲组笔试成绩的众数是 ,中位数是 ;
(2) 乙组笔试成绩的众数是 ,中位数是 .
87
100
中位数乙:
甲组:74 87 87 87 90 95 96
乙组:41 84 88 97 100 100
87
92.5
三、描述数据
小组 笔试平均分 (分) 小组操作得分 (分) 加权平均分
(4:6)
甲组 88 44 61.6
乙组 85 47 62.2
众数、中位数
中位数甲:87
组的笔试成绩稳定性高.
甲
小组 笔试平均分(分) 小组操作 得分(分) 加权平均分 (4:6) 众数 中位数
甲组 88 44 61.6 87 87
乙组 85 47 62.2 100 92.5
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
三、描述数据
组的笔试成绩稳定性高.
甲
< ,
方 差
三、描述数据
小组 笔试平均分(分) 小组操作 得分(分) 加权平均分 (4:6) 众数 中位数
甲组 88 44 61.6 87 87
乙组 85 47 62.2 100 92.5
笔试成绩(单位:分)如下:
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
甲组:96 95 74 87 87 90 87
乙组:84 100 41 100 97 88
甲组 笔试平均分 88
中位数 87
众数 87
方差 45.14
乙组 笔试平均分 85
中位数 92.5
众数 100
方差 423.33
估计在88分左右
稳
估计在92分左右
不稳定
√
四、分析数据
小组 笔试平均分 (分) 小组操作得分 (分) 加权平均分
(4:6)
甲组 88 44 61.6
乙组 85 47 62.2
平均数
数据的分析
数据的集中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
用样本平均数估计总体平均数
用样本方差估计总体方差
小结
《根据死亡公告的自然和政治的观察》
统计学的发展
古 往
格朗特 (J. Graunt , 1620 -1674) .
整理数据
用数学揭示数字之间的关系
发现新的真相
提取数据信息
统计学的发展
古 往
高斯 (C. F.Gass , 1777 -1855) .
勒让德 (A. -M.Legendre , 1752 -1833) .
关于最小二乘法的工作
皮尔逊 (K. Pearson , 1857 -1936) .
总体
根据样本对总体进行推断
对数据的推断
费希尔 (R.A. Fisher , 1890 -1962) .
试验设计分支及相应的方差分析方法等
统计学的发展
今 来
克拉默 (H. Cramer , 1893 -1985) .
1946年《统计学的数学方法》
数
据
初中的统计学
收集数据
整理数据
描述数据
分析数据
1. 举例说明平均数、中位数、众数的意义;
2. 算术平均数和加权平均数有什么联系和区别?举例说明加权平均数中“权”的意义;
3. 举例说明怎样用方差刻画数据的波动程度;
4. 举例说明刻画数据特征的量在决策中的作用;
5. 你认为统计学在生活中有什么意义和价值?
学后反思
课本
P136 复习巩固 第1题
P137 综合运用 第6题
课后作业
