沪科版八年级数学下册 专题:特殊四边形动点问题 课件(共34张PPT)
文档属性
| 名称 | 沪科版八年级数学下册 专题:特殊四边形动点问题 课件(共34张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览





文档简介
(共34张PPT)
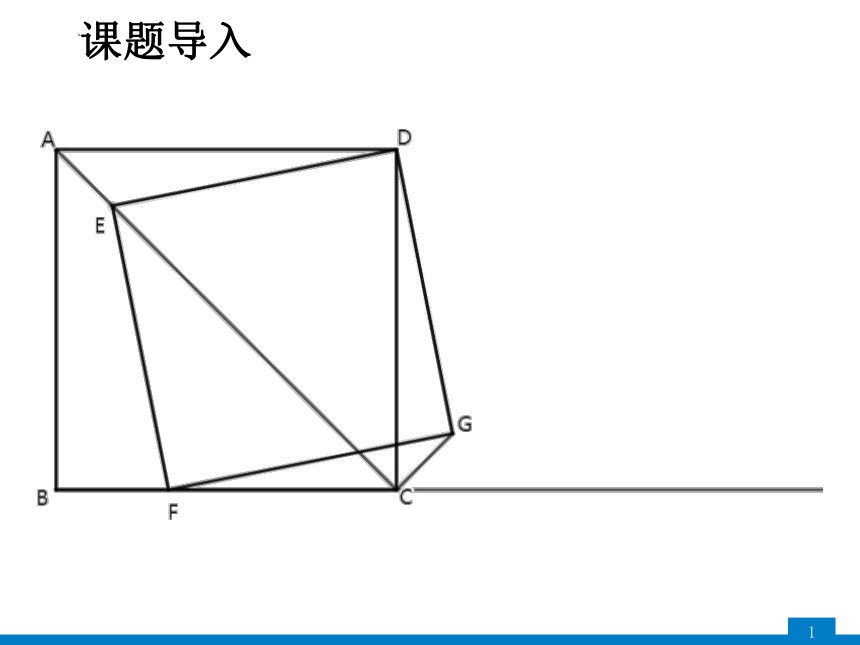
课题导入
课题导入
特殊四边形动点问题
会运用特殊平行四边形的性质解决实际问题
目标引领
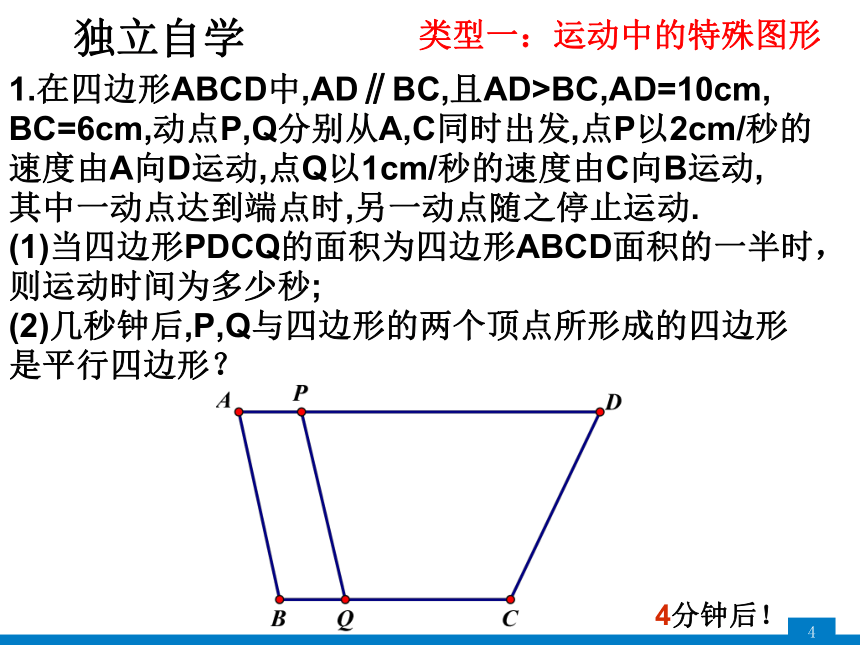
1.在四边形ABCD中,AD∥BC,且AD>BC,AD=10cm,
BC=6cm,动点P,Q分别从A,C同时出发,点P以2cm/秒的
速度由A向D运动,点Q以1cm/秒的速度由C向B运动,
其中一动点达到端点时,另一动点随之停止运动.
(1)当四边形PDCQ的面积为四边形ABCD面积的一半时,则运动时间为多少秒;
(2)几秒钟后,P,Q与四边形的两个顶点所形成的四边形
是平行四边形?
独立自学
4分钟后!
类型一:运动中的特殊图形
2.如图,已知平行四边形ABCD的对角线AC,BD相交于O,AC=20cm,BD=12cm,两动点E,F同时分别以2cm/s的速度从点A,C出发在线段AC上运动.
(1)求证:当E,F运动过程中不与点O重合时,四边形BEDF一定为平行四边形;
(2)当E,F运动时间t为何值时,四边形BEDF为矩形
引导探究
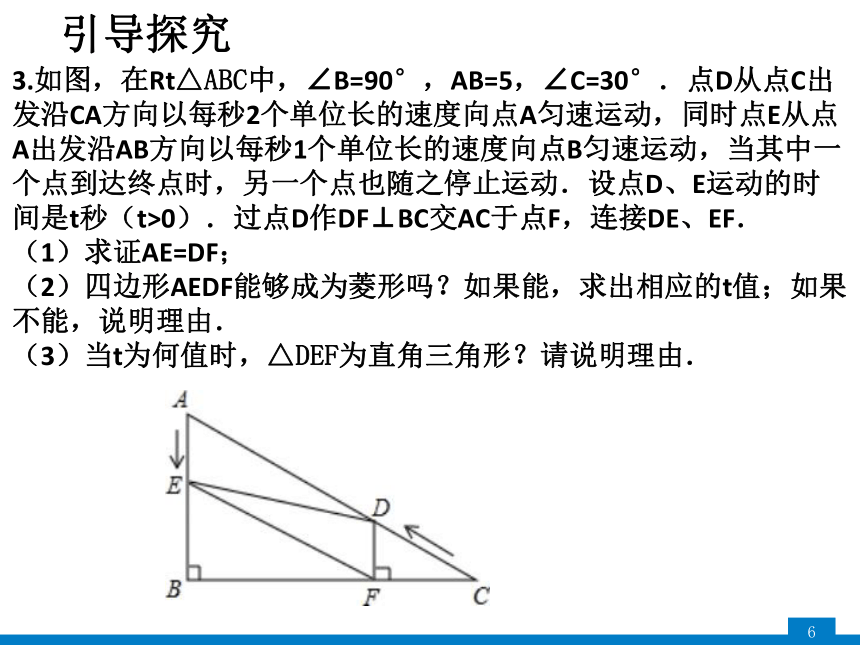
3.如图,在Rt△ABC中,∠B=90°,AB=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC交AC于点F,连接DE、EF.
(1)求证AE=DF;
(2)四边形AEDF能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
引导探究
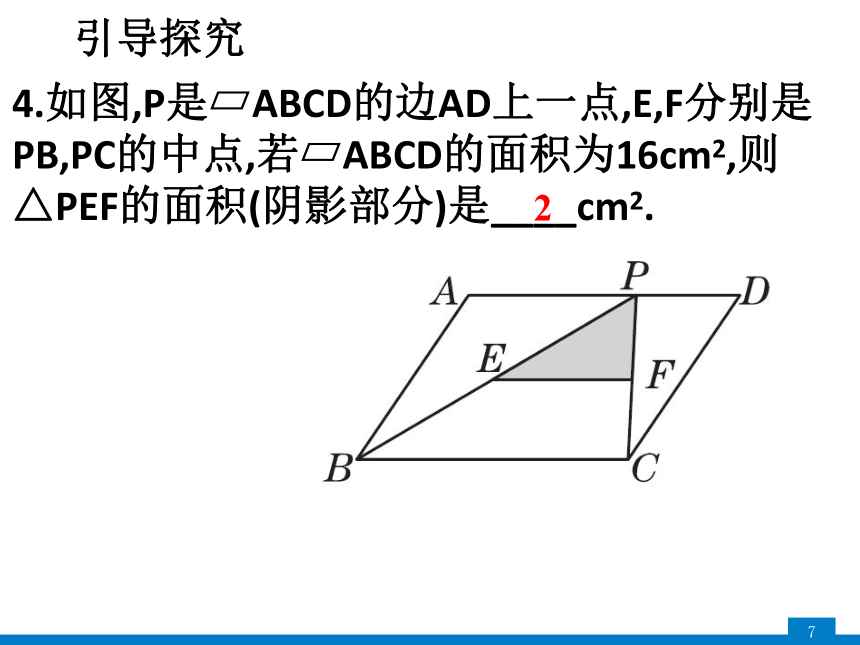
4.如图,P是 ABCD的边AD上一点,E,F分别是
PB,PC的中点,若 ABCD的面积为16cm2,则
△PEF的面积(阴影部分)是____cm2.
2
引导探究
类型二:动点与函数
5.如图,在菱形ABCD中,M是AD的中点,点P由点A出发,沿A→B→C→D做匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的大致图象是( )
D
引导探究
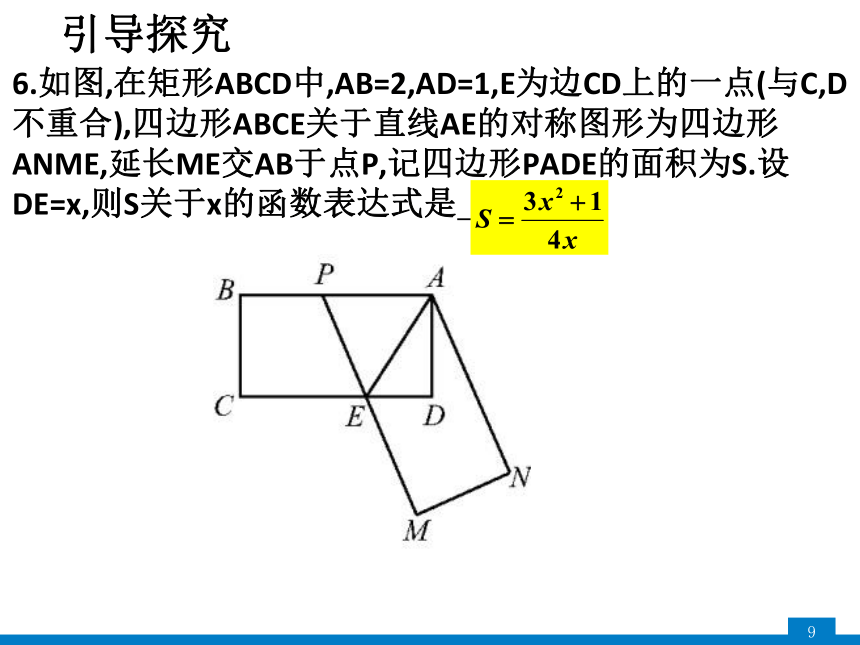
6.如图,在矩形ABCD中,AB=2,AD=1,E为边CD上的一点(与C,D不重合),四边形ABCE关于直线AE的对称图形为四边形ANME,延长ME交AB于点P,记四边形PADE的面积为S.设DE=x,则S关于x的函数表达式是 .
引导探究
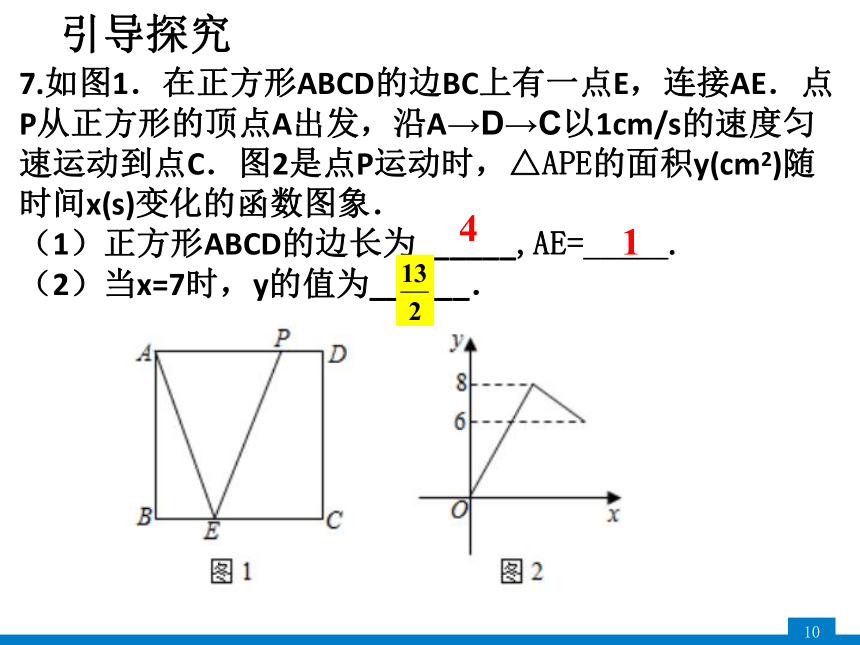
7.如图1.在正方形ABCD的边BC上有一点E,连接AE.点P从正方形的顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C.图2是点P运动时,△APE的面积y(cm2)随时间x(s)变化的函数图象.
(1)正方形ABCD的边长为______,AE=_____.
(2)当x=7时,y的值为______.
4
1
引导探究
类型三:动点求值
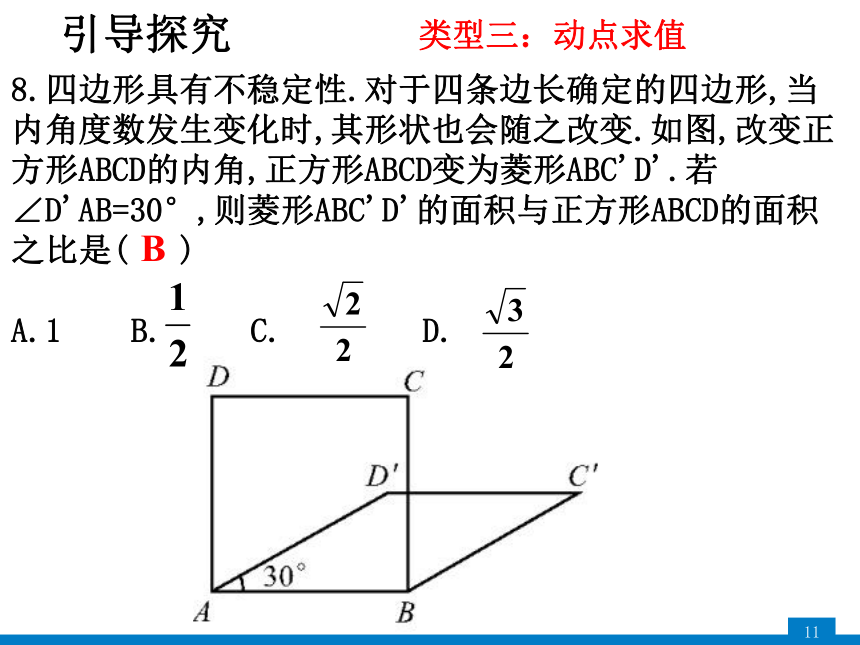
8.四边形具有不稳定性.对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D'.若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是( )
A.1 B. C. D.
B
引导探究
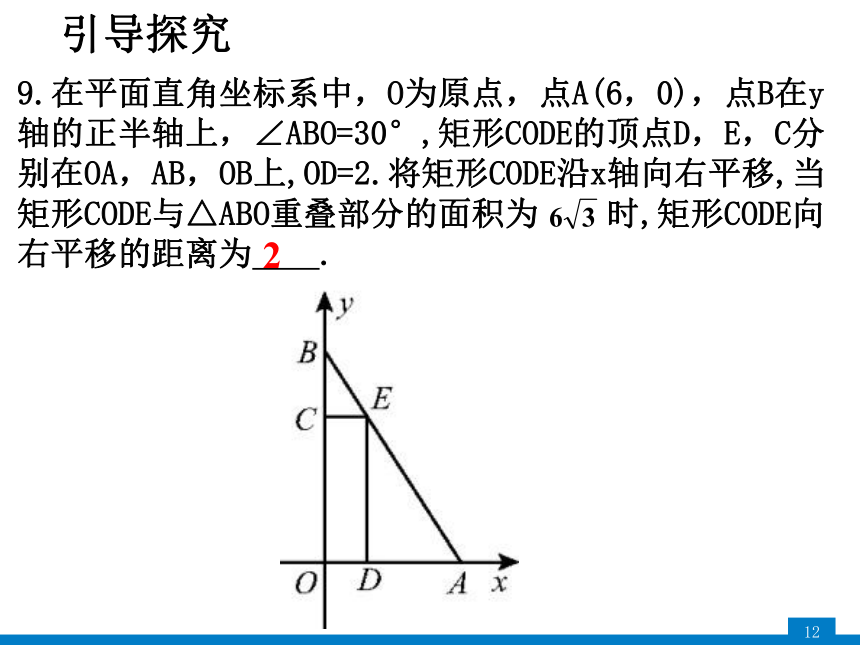
9.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°,矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.将矩形CODE沿x轴向右平移,当矩形CODE与△ABO重叠部分的面积为 时,矩形CODE向右平移的距离为 .
2
引导探究
10.如图,四边形ABCD是边长为2的正方形,E是边BC上一个动点(不与点B,C重合),∠AEF=90°,且EF交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:
①∠BAE=∠CEG;②AE=EF;③∠DAF=∠CFE;④BE2+AD2=AF2.
其中正确结论的序号是 .
引导探究
类型四:动点求最值---矩形对角线
11.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于__.
引导探究
类型四:动点求最值---直角三角形斜边中线
12.如图,∠MON=90°,动点A、B分别位于射线OM、ON上,矩形ABCD的边AB=6,BC=4,则线段OC长的最大值是( )
A.10 B.8 C.6 D.5
B
引导探究
类型四:动点求最值---中位线
13.如图,在菱形ABCD中,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC=2 ,则GH的最小值为_______.
引导探究
类型四:动点求最值---将军饮马
14.如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△PAB= S△PCD,则PC+PD的最小值是________.
引导探究
15.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),当EP+BP最短时,点P的坐标为_______.
引导探究
16.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0 B.4 C.6 D.8
D
引导探究
17.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD方向平移,得到△EGF,连接EC,GC,则EC+GC的最小值为 .
引导探究
18.如图,在矩形ABCD中,BC=10,∠ABD=30°,若M,N分别是线段BD,AB上的两个动点,则AM+MN的最小值为 .
类型四:动点求最值---垂线段最短
15
引导探究
类型四:动点求最值---利用轨迹
19.如图,在矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB.若PB的最小值为5 ,则AD的长为 ( )
A.5 B.6 C.7 D.8
A
P点的运动轨迹为△DEF的中位线
引导探究
20.如图,点E是边长为8的正方形ABCD的对角线BD上的动点,以AE为边向左侧作正方形AEFG,点P为AD的中点,连接PG,在点E的运动过程中,线段PG的最小值是( )
G点的运动轨迹为正方形外角的角平分线
C
引导探究
21.如图,正方形ABCD,边长为7,点E在边BC上,BE=2,点F是AB边上一动点,连接EF,以EF为边向右作等边△EFG,连接CG,线段CG的最小值是___________.
引导探究
类型五:运动中的数量关系
22.P是 ABCD的对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为E,F.O为AC的中点.
(1)如图1,当点P与点O重合时,线段OE和OF的关系是 ;
(2)当点P运动到如图2所示的位置时,请在图中补全图形,并通过证明判断(1)中的结论是否仍然成立
(3)如图3,点P在线段OA的延长线上运动,当
∠OEF=30°时,试探究线段CF,AE,OE之间的关系.
引导探究
谈一谈你有什么收获
目标升华
(1)如图,点O为 ABCD的对角线AC,BD的交点.
∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.求EF的长
(2)若△AOE的面积为S1,△COF的面积为S2,
S1+S2的值是否发生变化 若不变,求出这个不变的
值;若变化,请说明随着DE的增大,S1+S2的值是如何
发生变化的?
当堂诊学
2.在菱形ABCD中,∠B=60°,动点E在边BC上,动点F
在边CD上.(1)如图①,若E是BC的中点,∠AEF=60°,
求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
当堂诊学
3.已知正方形ABCD,P为射线AB上一点,以BP为边作
正方形BPEF,使点F在线段CB的延长线上,连接EA,EC,
AC.
(1)如图①,若点P在线段AB的延长线上,判断△ACE的
形状,并说明理由.
②当AB=BP时,请直接写出∠CAE的度数.
(2)如图②,已知点P在线段AB上.
①若点P是线段AB的中点,判断
△ACE的形状,并说明理由;
当堂诊学
4.已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的
垂直平分线EF分别交AD,BC于点E,F,垂足为O.
如图①,连接AF,CE.
(1)四边形AFCE是什么特殊四边形 请说明理由;
(2)求AF的长;
当堂诊学
引导探究
拓展拔高
引导探究
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10 cm,AD=8 cm,E,F分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每
秒2 cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3 cm的速度向C点运动,H,P两点同时出发,运动时间为t秒,当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
当堂诊学
(1)如图①,纸片 ABCD中,AD=5,S ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
①求证:四边形AFF′D是菱形;
②求四边形AFF′D的两条对角线的长.
当堂诊学
课题导入
课题导入
特殊四边形动点问题
会运用特殊平行四边形的性质解决实际问题
目标引领
1.在四边形ABCD中,AD∥BC,且AD>BC,AD=10cm,
BC=6cm,动点P,Q分别从A,C同时出发,点P以2cm/秒的
速度由A向D运动,点Q以1cm/秒的速度由C向B运动,
其中一动点达到端点时,另一动点随之停止运动.
(1)当四边形PDCQ的面积为四边形ABCD面积的一半时,则运动时间为多少秒;
(2)几秒钟后,P,Q与四边形的两个顶点所形成的四边形
是平行四边形?
独立自学
4分钟后!
类型一:运动中的特殊图形
2.如图,已知平行四边形ABCD的对角线AC,BD相交于O,AC=20cm,BD=12cm,两动点E,F同时分别以2cm/s的速度从点A,C出发在线段AC上运动.
(1)求证:当E,F运动过程中不与点O重合时,四边形BEDF一定为平行四边形;
(2)当E,F运动时间t为何值时,四边形BEDF为矩形
引导探究
3.如图,在Rt△ABC中,∠B=90°,AB=5,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC交AC于点F,连接DE、EF.
(1)求证AE=DF;
(2)四边形AEDF能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
引导探究
4.如图,P是 ABCD的边AD上一点,E,F分别是
PB,PC的中点,若 ABCD的面积为16cm2,则
△PEF的面积(阴影部分)是____cm2.
2
引导探究
类型二:动点与函数
5.如图,在菱形ABCD中,M是AD的中点,点P由点A出发,沿A→B→C→D做匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的大致图象是( )
D
引导探究
6.如图,在矩形ABCD中,AB=2,AD=1,E为边CD上的一点(与C,D不重合),四边形ABCE关于直线AE的对称图形为四边形ANME,延长ME交AB于点P,记四边形PADE的面积为S.设DE=x,则S关于x的函数表达式是 .
引导探究
7.如图1.在正方形ABCD的边BC上有一点E,连接AE.点P从正方形的顶点A出发,沿A→D→C以1cm/s的速度匀速运动到点C.图2是点P运动时,△APE的面积y(cm2)随时间x(s)变化的函数图象.
(1)正方形ABCD的边长为______,AE=_____.
(2)当x=7时,y的值为______.
4
1
引导探究
类型三:动点求值
8.四边形具有不稳定性.对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D'.若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是( )
A.1 B. C. D.
B
引导探究
9.在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°,矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.将矩形CODE沿x轴向右平移,当矩形CODE与△ABO重叠部分的面积为 时,矩形CODE向右平移的距离为 .
2
引导探究
10.如图,四边形ABCD是边长为2的正方形,E是边BC上一个动点(不与点B,C重合),∠AEF=90°,且EF交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:
①∠BAE=∠CEG;②AE=EF;③∠DAF=∠CFE;④BE2+AD2=AF2.
其中正确结论的序号是 .
引导探究
类型四:动点求最值---矩形对角线
11.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D在AB边上,DE⊥AC,DF⊥BC,垂足分别为点E、F,连接EF,则线段EF的最小值等于__.
引导探究
类型四:动点求最值---直角三角形斜边中线
12.如图,∠MON=90°,动点A、B分别位于射线OM、ON上,矩形ABCD的边AB=6,BC=4,则线段OC长的最大值是( )
A.10 B.8 C.6 D.5
B
引导探究
类型四:动点求最值---中位线
13.如图,在菱形ABCD中,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC=2 ,则GH的最小值为_______.
引导探究
类型四:动点求最值---将军饮马
14.如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△PAB= S△PCD,则PC+PD的最小值是________.
引导探究
15.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),当EP+BP最短时,点P的坐标为_______.
引导探究
16.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0 B.4 C.6 D.8
D
引导探究
17.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD方向平移,得到△EGF,连接EC,GC,则EC+GC的最小值为 .
引导探究
18.如图,在矩形ABCD中,BC=10,∠ABD=30°,若M,N分别是线段BD,AB上的两个动点,则AM+MN的最小值为 .
类型四:动点求最值---垂线段最短
15
引导探究
类型四:动点求最值---利用轨迹
19.如图,在矩形ABCD中,AB:AD=2:1,点E为AB的中点,点F为EC上一个动点,点P为DF的中点,连接PB.若PB的最小值为5 ,则AD的长为 ( )
A.5 B.6 C.7 D.8
A
P点的运动轨迹为△DEF的中位线
引导探究
20.如图,点E是边长为8的正方形ABCD的对角线BD上的动点,以AE为边向左侧作正方形AEFG,点P为AD的中点,连接PG,在点E的运动过程中,线段PG的最小值是( )
G点的运动轨迹为正方形外角的角平分线
C
引导探究
21.如图,正方形ABCD,边长为7,点E在边BC上,BE=2,点F是AB边上一动点,连接EF,以EF为边向右作等边△EFG,连接CG,线段CG的最小值是___________.
引导探究
类型五:运动中的数量关系
22.P是 ABCD的对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为E,F.O为AC的中点.
(1)如图1,当点P与点O重合时,线段OE和OF的关系是 ;
(2)当点P运动到如图2所示的位置时,请在图中补全图形,并通过证明判断(1)中的结论是否仍然成立
(3)如图3,点P在线段OA的延长线上运动,当
∠OEF=30°时,试探究线段CF,AE,OE之间的关系.
引导探究
谈一谈你有什么收获
目标升华
(1)如图,点O为 ABCD的对角线AC,BD的交点.
∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.求EF的长
(2)若△AOE的面积为S1,△COF的面积为S2,
S1+S2的值是否发生变化 若不变,求出这个不变的
值;若变化,请说明随着DE的增大,S1+S2的值是如何
发生变化的?
当堂诊学
2.在菱形ABCD中,∠B=60°,动点E在边BC上,动点F
在边CD上.(1)如图①,若E是BC的中点,∠AEF=60°,
求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
当堂诊学
3.已知正方形ABCD,P为射线AB上一点,以BP为边作
正方形BPEF,使点F在线段CB的延长线上,连接EA,EC,
AC.
(1)如图①,若点P在线段AB的延长线上,判断△ACE的
形状,并说明理由.
②当AB=BP时,请直接写出∠CAE的度数.
(2)如图②,已知点P在线段AB上.
①若点P是线段AB的中点,判断
△ACE的形状,并说明理由;
当堂诊学
4.已知,矩形ABCD中,AB=4 cm,BC=8 cm,AC的
垂直平分线EF分别交AD,BC于点E,F,垂足为O.
如图①,连接AF,CE.
(1)四边形AFCE是什么特殊四边形 请说明理由;
(2)求AF的长;
当堂诊学
引导探究
拓展拔高
引导探究
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10 cm,AD=8 cm,E,F分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每
秒2 cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3 cm的速度向C点运动,H,P两点同时出发,运动时间为t秒,当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
当堂诊学
(1)如图①,纸片 ABCD中,AD=5,S ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
①求证:四边形AFF′D是菱形;
②求四边形AFF′D的两条对角线的长.
当堂诊学
