湘教版数学七年级下册 第1章 二元一次方程组 章末复习 课件(共23张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 第1章 二元一次方程组 章末复习 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
章末复习
湘教版 七年级下册
1.含有____未知数,且含有未知数的项的次数都是______的方程叫_____________.
2.使二元一次方程的两边值_____的一对未知数的值,叫做________________
3.由_________组成,且含有____未知数的方程组,叫做_________________.
4. 同时满足二元一次方程组中各个方程的解,叫做______________________.
两个
二元一次方程
一次
相等
二元一次方程的解
一次方程
两个
二元一次方程组
二元一次方程组的解
复习导入
1.下列是二元一次方程的是 ( )
2.下列各方程组中,属于二元一次方程组的是( )
B
C
3.下列各对数是二元一次方程2x-5y=3的解的是 ( )
4.二元一次方程组 的解( )
D
D
5.写出一个解为 的二元一次
方程组--------
6.已知二元一次方程:2x+3y=15
(1)用含x的代数式表示y;
(2)求出该方程的正整数解;
x=3
y=3
x=6
y=1
或者
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法:加减消元法
巩固旧识
(2)
例1.用适当的方法解下列方程组:
⑴
①
②
②
①
3.已知 ,
①-②得:
⑴
(2)
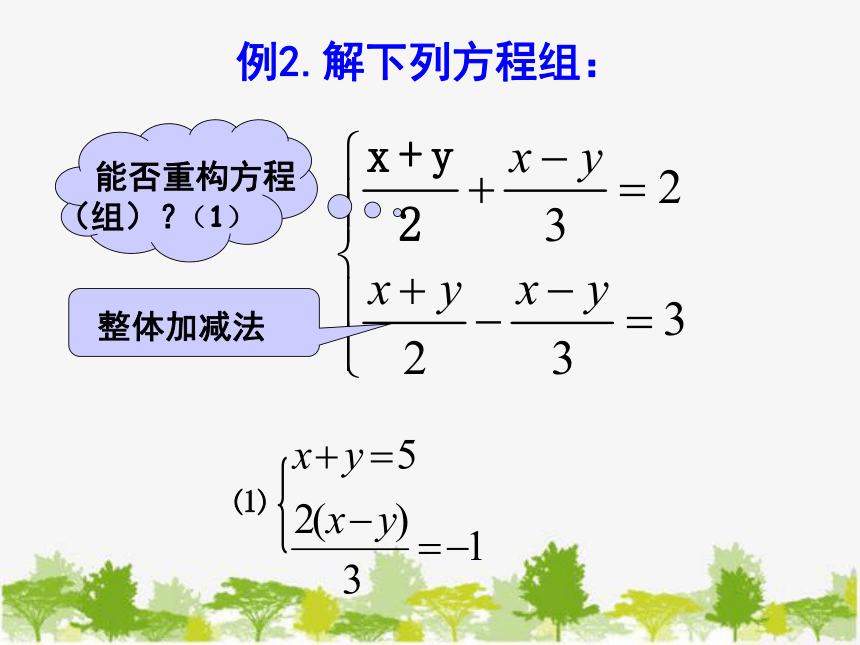
例2.解下列方程组:
能否重构方程(组)?
(1)
整体加减法
⑴
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①
②
。
整体代入
复习训练
4.已知 是方程
的解,求m+n的值。
灵活应用
根据题意,灵活组建二元一次方程组
①+②得 m+n=7
①
②
5.当a为何值时,方程组
的解x、y的值互为相反数。
灵活应用
①
②
4、方程组 与方程组
的解相同,求a,b的值。
灵活应用
灵活应用
5、解关于x、y的方程组 时,
小明求得正确的解是 ,
而小马因看错系数 c 解得 ,
试求a,b,c的值。
拓展提高
1.已知
,则
。
6
2.已知 x + 4y = 0 (y≠0),求 的值.
y – 2z = 0
3.阅读下列解题过程:
解方程组 23x+17y=63①
17x+23y=57②
解:①+②,得:40x+40y=120
即:x+y=3③
①-②,得:6x-6y=6
即:x-y=1 ④
③+④得:2x=4 ∴x=2
③-④得:2y=2 ∴y=1
∴ x=2
y=1
请你运用以上
解法解方程组
2010x+2011y =2011
2011x+2010y=2010
1.已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为
相 反数,求x、y的值。
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
成为有数学素养的高素质人才
拓展解题技能、提升数学思想
熟练掌握基本计算、方法
夯 实 基 础
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
1.已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为
相 反数,求x、y的值。
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,求x、y的值。
解:由已知得
①
②
由①得: ③
把③代入②得:
解得:
把 代入③得:
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
章末复习
湘教版 七年级下册
1.含有____未知数,且含有未知数的项的次数都是______的方程叫_____________.
2.使二元一次方程的两边值_____的一对未知数的值,叫做________________
3.由_________组成,且含有____未知数的方程组,叫做_________________.
4. 同时满足二元一次方程组中各个方程的解,叫做______________________.
两个
二元一次方程
一次
相等
二元一次方程的解
一次方程
两个
二元一次方程组
二元一次方程组的解
复习导入
1.下列是二元一次方程的是 ( )
2.下列各方程组中,属于二元一次方程组的是( )
B
C
3.下列各对数是二元一次方程2x-5y=3的解的是 ( )
4.二元一次方程组 的解( )
D
D
5.写出一个解为 的二元一次
方程组--------
6.已知二元一次方程:2x+3y=15
(1)用含x的代数式表示y;
(2)求出该方程的正整数解;
x=3
y=3
x=6
y=1
或者
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法:加减消元法
巩固旧识
(2)
例1.用适当的方法解下列方程组:
⑴
①
②
②
①
3.已知 ,
①-②得:
⑴
(2)
例2.解下列方程组:
能否重构方程(组)?
(1)
整体加减法
⑴
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①
②
。
整体代入
复习训练
4.已知 是方程
的解,求m+n的值。
灵活应用
根据题意,灵活组建二元一次方程组
①+②得 m+n=7
①
②
5.当a为何值时,方程组
的解x、y的值互为相反数。
灵活应用
①
②
4、方程组 与方程组
的解相同,求a,b的值。
灵活应用
灵活应用
5、解关于x、y的方程组 时,
小明求得正确的解是 ,
而小马因看错系数 c 解得 ,
试求a,b,c的值。
拓展提高
1.已知
,则
。
6
2.已知 x + 4y = 0 (y≠0),求 的值.
y – 2z = 0
3.阅读下列解题过程:
解方程组 23x+17y=63①
17x+23y=57②
解:①+②,得:40x+40y=120
即:x+y=3③
①-②,得:6x-6y=6
即:x-y=1 ④
③+④得:2x=4 ∴x=2
③-④得:2y=2 ∴y=1
∴ x=2
y=1
请你运用以上
解法解方程组
2010x+2011y =2011
2011x+2010y=2010
1.已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为
相 反数,求x、y的值。
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
成为有数学素养的高素质人才
拓展解题技能、提升数学思想
熟练掌握基本计算、方法
夯 实 基 础
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
1.已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为
相 反数,求x、y的值。
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,
求x、y的值。
4x+3y-5=0
x-3y-4=0
y+5=2x
3x=2-4y
(X-3Y-4)2
掌握基本方法
2.已知 3ay+5b3x与-5a2xb2-4y是同类项,求x、y的值。
解:由已知得
①
②
由①得: ③
把③代入②得:
解得:
把 代入③得:
通过这节课的学习活动,你有什么收获?
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
