21.2.2 公式法 课件(共26张PPT)
文档属性
| 名称 | 21.2.2 公式法 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
人教版 九年级上
21.2.2 公式法
新知导入
情境引入
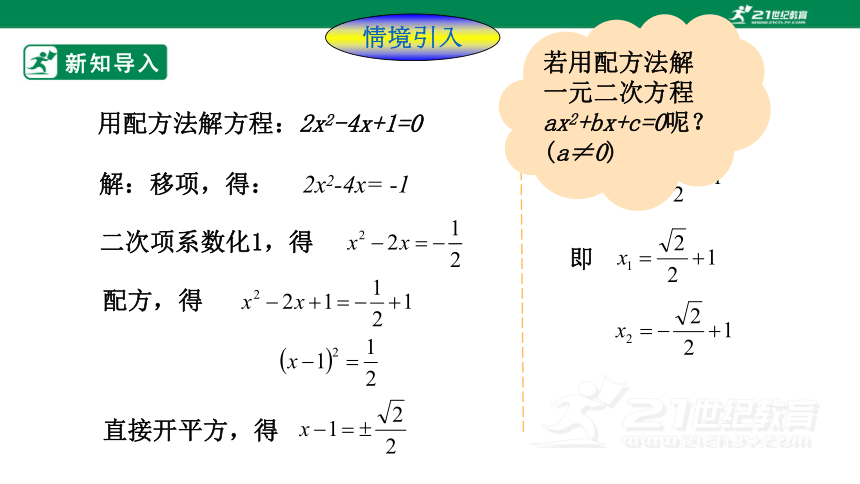
用配方法解方程:2x2-4x+1=0
解:移项,得:
配方,得
二次项系数化1,得
2x2-4x= -1
直接开平方,得
即
若用配方法解一元二次方程ax2+bx+c=0呢?
(a≠0)
新知导入
合作学习
化:把原方程化成 x+px+q = 0 的形式。
移项:把常数项移到方程的右边,如x2+px =-q。
配方:方程两边都加上一次项系数一半的平方。
开方:根据平方根的意义,方程两边开平方。
求解:解一元一次方程。
定解:写出原方程的解。
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+ ( )2 = -q+ ( )2
( x+ )2 =-q+ ( )2
新知讲解
任何一个一元二次方程都可以写成一般形式:
ax2+bx+c=0(a≠0)
我们学习了用配方法解数字系数的一元二次方程,能否也用配方法解一般形式的一元二次方程呢?
思考:
新知讲解
★ 用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
二次项系数化为1,得
解:
移项,得
配方,得
即 ①
活动1-交流讨论:
新知讲解
活动2-观察分析:
问题:对于方程①接下来能用直接开平方解吗?
∵a ≠0,∴4a2>0.
式子b2-4ac 的值有一下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
方程有两个不等的实数根:
新知讲解
合作探究
(2)b2-4ac =0
这时 =0,由①可知,方程有两个相等的实数根 x1=x2=- .
(3)b2-4ac <0
这时 <0,由①可知 <0 ,
而x取任何实数都不能使 <0 ,因此方程无实数根.
一般地,式子b2 -4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用希腊字母“△”表示它,即:△=b2-4ac
新知讲解
提炼概念
活动3-归纳总结:
由上可知:
当△>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根;
当△=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根;
当△<0时,方程ax2+bx+c=0(a≠0)无实数根。
新知讲解
按要求完成下列表格:
△的值
21
-4
根的情况
有两个不相等的实数根
有两个相等的实数根
没有实数根
0
小试牛刀
新知讲解
由上可知,当 △≥0时,方程ax2+bx+c=0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程ax2+bx+c=0 的求根公式.
用求根公式解一元二次方程的方法叫做公式法.
新知讲解
典例精讲
例2、用公式法解下列方程:
(1)x2-4x-7=0;
方程有两个不相等的实数根.
解:a=1,b=-4,c=-7
b2-4ac=(-4)2-4×1×(-7)=44>0.
即
新知讲解
方程有两个相等的实数根
x1=x2
(2)2x2-2 x+1=0;
解:a=2,b=-2 ,c=1
b2-4ac=(-2 )2-4×2×1=0.
新知讲解
(3)5x2-3x=x+1;
=
即
a=5,b=-4,c=-1
解:方程化为 5x2-4x-1=0
方程有两个不相等的实数根
b2-4ac=(-4)2-4×5×(-1)=36>0.
新知讲解
(4)x2+17=8x.
方程无实数根.
a=1,b=-8,c=17
b2-4ac=(-8)2-4×1×17=-4<0.
解:方程化为 x2-8x+17=0
★归纳总结:运用公式法解一元二次方程的步骤:①要将方程化为一般式确定a、b、c的值;
②判定△=b2 - 4ac的符号;③当 △≥0时,直接用求根公式;△<0,则方程没有实数根。
新知讲解
归纳概念
思考:运用公式法解一元二次方程时,有哪些注意事项?解题步骤有哪些?
步骤:1.变形:化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算: =b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
易错点:计算Δ的值时,注意a,b,c符号的问题.
课堂练习
C
1.用公式法解方程3x-7=6x2时,a、b、c的值分别是( )
A.3、7、-6 B.3、-7、-6
C.3、-7、6 D.3、7、-6
课堂练习
2、选择题(请用最快的速度,把“有两个实数根”的方程和“没有实数根”的方程的序号选入相应的括号内)
(1) (2)
(3) (4)
有两个实数根的方程的序号是( )
没有实数根的方程的序号是( )
(3)
(2)
(4)
(1)
课堂练习
3. 用公式法解下列方程:
(1) 5x2-3x-1=0 (2) (3)x2-8x=3x2+8
解:(1) a=5,b=-3,c=-1
△=b2-4ac=(-3)2-4×5×(-1)=29>0
方程有两个不相等的实数根.
即
课堂练习
△=b2-4ac=
(2) 方程化为
方程无实数根.
课堂练习
方程有两个相等的实数根.
a=-2,b=-8,c=-8
△=b2-4ac=(-8)2-4×(-2)×(-8)=0
(3) 方程化为-2x2-8x-8=0
课堂练习
4、(1)关于x的一元二次方程 有两个实根,则m的取值范围是 .
(2)若关于x的一元二次方程(k-1)x2-2kx+k=2有实数根.求m的取值范围.
解:化为一般式(k-1)x2-2kx+k-2=0.
△=4k2 4(k 1)(k 2)≥0,且k-1≠0
解得
且k≠1.
课堂总结
公式法
求根公式
步骤
一化(一般形式);
二定(系数值);
三求( Δ值);
四判(方程根的情况);
五代(求根公式计算).
根的判别式b2-4ac
务必将方程化为一般形式
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上
21.2.2 公式法
新知导入
情境引入
用配方法解方程:2x2-4x+1=0
解:移项,得:
配方,得
二次项系数化1,得
2x2-4x= -1
直接开平方,得
即
若用配方法解一元二次方程ax2+bx+c=0呢?
(a≠0)
新知导入
合作学习
化:把原方程化成 x+px+q = 0 的形式。
移项:把常数项移到方程的右边,如x2+px =-q。
配方:方程两边都加上一次项系数一半的平方。
开方:根据平方根的意义,方程两边开平方。
求解:解一元一次方程。
定解:写出原方程的解。
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+ ( )2 = -q+ ( )2
( x+ )2 =-q+ ( )2
新知讲解
任何一个一元二次方程都可以写成一般形式:
ax2+bx+c=0(a≠0)
我们学习了用配方法解数字系数的一元二次方程,能否也用配方法解一般形式的一元二次方程呢?
思考:
新知讲解
★ 用配方法解一般形式的一元二次方程 ax2+bx+c=0 (a≠0).
二次项系数化为1,得
解:
移项,得
配方,得
即 ①
活动1-交流讨论:
新知讲解
活动2-观察分析:
问题:对于方程①接下来能用直接开平方解吗?
∵a ≠0,∴4a2>0.
式子b2-4ac 的值有一下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
方程有两个不等的实数根:
新知讲解
合作探究
(2)b2-4ac =0
这时 =0,由①可知,方程有两个相等的实数根 x1=x2=- .
(3)b2-4ac <0
这时 <0,由①可知 <0 ,
而x取任何实数都不能使 <0 ,因此方程无实数根.
一般地,式子b2 -4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用希腊字母“△”表示它,即:△=b2-4ac
新知讲解
提炼概念
活动3-归纳总结:
由上可知:
当△>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根;
当△=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根;
当△<0时,方程ax2+bx+c=0(a≠0)无实数根。
新知讲解
按要求完成下列表格:
△的值
21
-4
根的情况
有两个不相等的实数根
有两个相等的实数根
没有实数根
0
小试牛刀
新知讲解
由上可知,当 △≥0时,方程ax2+bx+c=0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程ax2+bx+c=0 的求根公式.
用求根公式解一元二次方程的方法叫做公式法.
新知讲解
典例精讲
例2、用公式法解下列方程:
(1)x2-4x-7=0;
方程有两个不相等的实数根.
解:a=1,b=-4,c=-7
b2-4ac=(-4)2-4×1×(-7)=44>0.
即
新知讲解
方程有两个相等的实数根
x1=x2
(2)2x2-2 x+1=0;
解:a=2,b=-2 ,c=1
b2-4ac=(-2 )2-4×2×1=0.
新知讲解
(3)5x2-3x=x+1;
=
即
a=5,b=-4,c=-1
解:方程化为 5x2-4x-1=0
方程有两个不相等的实数根
b2-4ac=(-4)2-4×5×(-1)=36>0.
新知讲解
(4)x2+17=8x.
方程无实数根.
a=1,b=-8,c=17
b2-4ac=(-8)2-4×1×17=-4<0.
解:方程化为 x2-8x+17=0
★归纳总结:运用公式法解一元二次方程的步骤:①要将方程化为一般式确定a、b、c的值;
②判定△=b2 - 4ac的符号;③当 △≥0时,直接用求根公式;△<0,则方程没有实数根。
新知讲解
归纳概念
思考:运用公式法解一元二次方程时,有哪些注意事项?解题步骤有哪些?
步骤:1.变形:化已知方程为一般形式;
2.确定系数:用a,b,c写出各项系数;
3.计算: =b2-4ac的值;
4.判断:若b2-4ac ≥0,则利用求根公式求出;
若b2-4ac<0,则方程没有实数根.
易错点:计算Δ的值时,注意a,b,c符号的问题.
课堂练习
C
1.用公式法解方程3x-7=6x2时,a、b、c的值分别是( )
A.3、7、-6 B.3、-7、-6
C.3、-7、6 D.3、7、-6
课堂练习
2、选择题(请用最快的速度,把“有两个实数根”的方程和“没有实数根”的方程的序号选入相应的括号内)
(1) (2)
(3) (4)
有两个实数根的方程的序号是( )
没有实数根的方程的序号是( )
(3)
(2)
(4)
(1)
课堂练习
3. 用公式法解下列方程:
(1) 5x2-3x-1=0 (2) (3)x2-8x=3x2+8
解:(1) a=5,b=-3,c=-1
△=b2-4ac=(-3)2-4×5×(-1)=29>0
方程有两个不相等的实数根.
即
课堂练习
△=b2-4ac=
(2) 方程化为
方程无实数根.
课堂练习
方程有两个相等的实数根.
a=-2,b=-8,c=-8
△=b2-4ac=(-8)2-4×(-2)×(-8)=0
(3) 方程化为-2x2-8x-8=0
课堂练习
4、(1)关于x的一元二次方程 有两个实根,则m的取值范围是 .
(2)若关于x的一元二次方程(k-1)x2-2kx+k=2有实数根.求m的取值范围.
解:化为一般式(k-1)x2-2kx+k-2=0.
△=4k2 4(k 1)(k 2)≥0,且k-1≠0
解得
且k≠1.
课堂总结
公式法
求根公式
步骤
一化(一般形式);
二定(系数值);
三求( Δ值);
四判(方程根的情况);
五代(求根公式计算).
根的判别式b2-4ac
务必将方程化为一般形式
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
