冀教版数学七年级下册 第六章 复习题(2)教案
文档属性
| 名称 | 冀教版数学七年级下册 第六章 复习题(2)教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览


文档简介
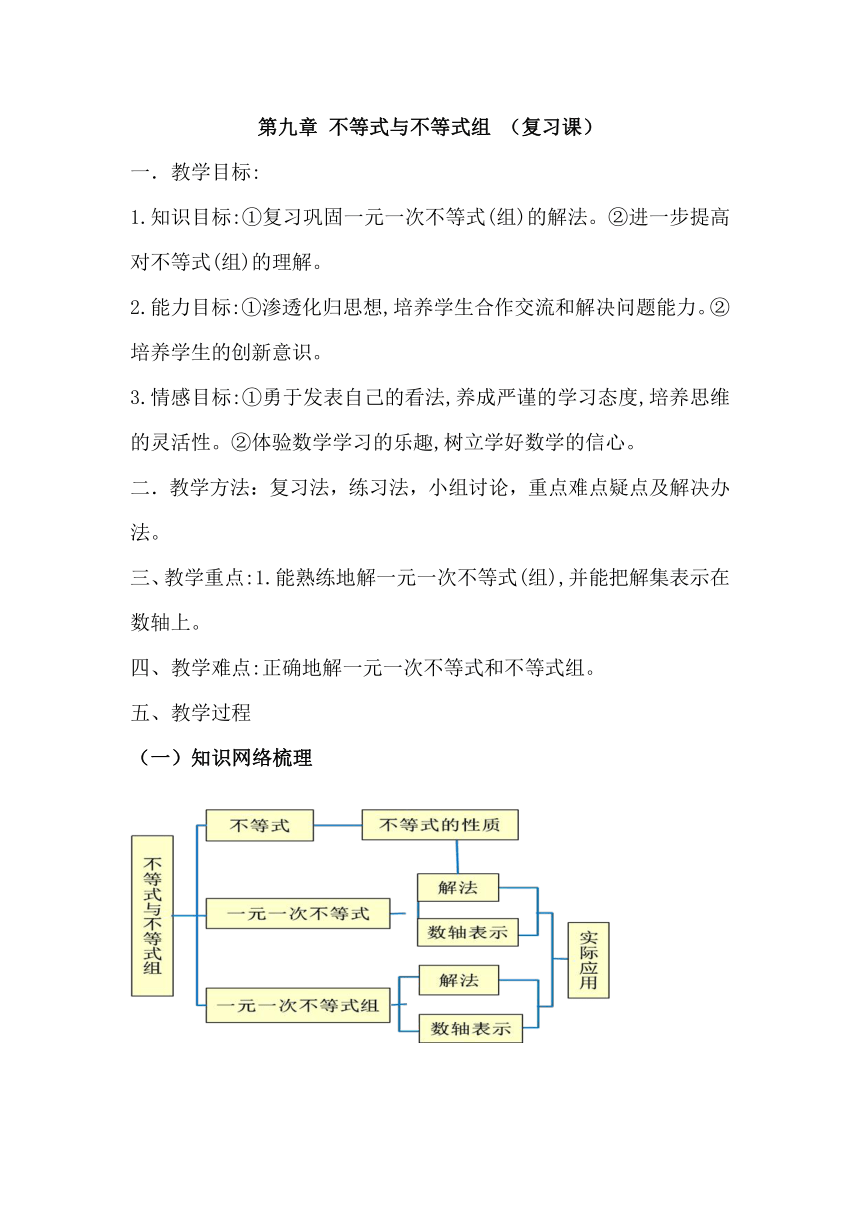
第九章 不等式与不等式组 (复习课)
一.教学目标:
1.知识目标:①复习巩固一元一次不等式(组)的解法。②进一步提高对不等式(组)的理解。
2.能力目标:①渗透化归思想,培养学生合作交流和解决问题能力。②培养学生的创新意识。
3.情感目标:①勇于发表自己的看法,养成严谨的学习态度,培养思维的灵活性。②体验数学学习的乐趣,树立学好数学的信心。
二.教学方法:复习法,练习法,小组讨论,重点难点疑点及解决办法。
三、教学重点:1.能熟练地解一元一次不等式(组),并能把解集表示在数轴上。
四、教学难点:正确地解一元一次不等式和不等式组。
五、教学过程
(一)知识网络梳理
(二)知识点归纳
一、基本概念
1、不等式, 2、不等式的解
3、不等式的解集 4、解不等式
5、一元一次不等式 6、一元一次不等式组
7、一元一次不等式组的解集 8、解一元一次不等式组
细心选一选
1.下列各式中,一元一次不等式的有( )
①3x-1≥4;② ;③ ;④
⑤ ;⑥;⑦x>0.
A.6个 B.5个 C.4个 D.3个
2.下列各数中,是不等式6x>8的解是( )
A.-1 B.0 C.1 D.2 3.不等式x<4的非负整数解的个数有( )
A.4个 B.3个 C.2个 D.1个
二、重要性质——不等式的性质
1)不等式两边都加上(或减去)同一个数(或式子),不等号的方向____.
2)不等式两边都乘 (或除以)同一个正数,不等号的方向____.
3)不等式两边都乘(或除以)同一个负数,不等号的方向____.
另外:不等式还具有______性. 如:当a>b, b>c时,则a>c.
认真填一填
用“>”或“<”填空:
(1)若x(3)若a>b,c<0,则ac____bc (4)若x(三)方法与过程
1、用数轴表示不等式的解集
步骤:画数轴,定界点,走方向。
规律:有等号(≤,≥)用实心圆点,无等号(<,>)用空心圆圈。
大于向右画,小于向左画。
细心看一看
请分别说出下列数轴所示的不等式的解集:
2、解一元一次不等式的步骤:
区别在哪里
在系数化为1时,要特别注意:不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
试一试
解:
3、解一元一次不等式组的步骤:
(1)先分别求出不等式组中各个不等式的解集。
(2)画数轴找出各个不等式的解集的公共部分。
(3)写出不等式组的解集。
4、求几个不等式的解集的公共部分的方法和规律:
(1)数轴法 (2)口诀法
求不等式组的解集的四种基本结果
试一试
1、不等式组 的解集是( )
2、不等式组 的解集在数轴上的表示正确的是( )
3、不等式组的解集是__________.
4、解不等式组
5、不等式 的最小整数解为( )
A、-1 B、0 C、2 D、3
6、不等式组的整数解为_______
(四)能力提升
1、若不等式ax+4<0的解集在数轴上表示如图所示,则( )
A、a>0 B、a<0 C、a=-2 D、a=2
2、关于x的不等式组 有解,那么m的取范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
(五)作业布置:
课本:P133 复习题 第1、3题
一.教学目标:
1.知识目标:①复习巩固一元一次不等式(组)的解法。②进一步提高对不等式(组)的理解。
2.能力目标:①渗透化归思想,培养学生合作交流和解决问题能力。②培养学生的创新意识。
3.情感目标:①勇于发表自己的看法,养成严谨的学习态度,培养思维的灵活性。②体验数学学习的乐趣,树立学好数学的信心。
二.教学方法:复习法,练习法,小组讨论,重点难点疑点及解决办法。
三、教学重点:1.能熟练地解一元一次不等式(组),并能把解集表示在数轴上。
四、教学难点:正确地解一元一次不等式和不等式组。
五、教学过程
(一)知识网络梳理
(二)知识点归纳
一、基本概念
1、不等式, 2、不等式的解
3、不等式的解集 4、解不等式
5、一元一次不等式 6、一元一次不等式组
7、一元一次不等式组的解集 8、解一元一次不等式组
细心选一选
1.下列各式中,一元一次不等式的有( )
①3x-1≥4;② ;③ ;④
⑤ ;⑥;⑦x>0.
A.6个 B.5个 C.4个 D.3个
2.下列各数中,是不等式6x>8的解是( )
A.-1 B.0 C.1 D.2 3.不等式x<4的非负整数解的个数有( )
A.4个 B.3个 C.2个 D.1个
二、重要性质——不等式的性质
1)不等式两边都加上(或减去)同一个数(或式子),不等号的方向____.
2)不等式两边都乘 (或除以)同一个正数,不等号的方向____.
3)不等式两边都乘(或除以)同一个负数,不等号的方向____.
另外:不等式还具有______性. 如:当a>b, b>c时,则a>c.
认真填一填
用“>”或“<”填空:
(1)若x
1、用数轴表示不等式的解集
步骤:画数轴,定界点,走方向。
规律:有等号(≤,≥)用实心圆点,无等号(<,>)用空心圆圈。
大于向右画,小于向左画。
细心看一看
请分别说出下列数轴所示的不等式的解集:
2、解一元一次不等式的步骤:
区别在哪里
在系数化为1时,要特别注意:不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
试一试
解:
3、解一元一次不等式组的步骤:
(1)先分别求出不等式组中各个不等式的解集。
(2)画数轴找出各个不等式的解集的公共部分。
(3)写出不等式组的解集。
4、求几个不等式的解集的公共部分的方法和规律:
(1)数轴法 (2)口诀法
求不等式组的解集的四种基本结果
试一试
1、不等式组 的解集是( )
2、不等式组 的解集在数轴上的表示正确的是( )
3、不等式组的解集是__________.
4、解不等式组
5、不等式 的最小整数解为( )
A、-1 B、0 C、2 D、3
6、不等式组的整数解为_______
(四)能力提升
1、若不等式ax+4<0的解集在数轴上表示如图所示,则( )
A、a>0 B、a<0 C、a=-2 D、a=2
2、关于x的不等式组 有解,那么m的取范围是( )
A、m>8 B、m≥8 C、m<8 D、m≤8
(五)作业布置:
课本:P133 复习题 第1、3题
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
