冀教版数学七年级下册 10.5 一元一次不等式组课件(共24张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 10.5 一元一次不等式组课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 633.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
10.5 一元一次不等式组
七年级数学·下 [冀教]
第十章 一元一次不等式和
一元一次不等式组
1.理解一元一次不等式组的概念,以及解集的意义.
2.掌握一元一次不等式组的解法,并能利用数轴确定其解集.
学习目标
3.会求一元一次不等式组的特殊解.
4.对含字母的一元一次不等式组,会根据解集求字母的取值范围.
1.不等式-X>-2的解是( )
A. X>2 B. X>-2
C. X<2 D. X<-2
C
2.如图所示,数轴表示
的是( )不等式的解集
A. X>-1 B. X<-1
C. X≤-1 D. X≥-1
-2 -1 0 1
D
知识回顾
1.掌握不等式的三条基本性质
不等式的性质1:不等式的两边加上(或减去)同一个数(或同一个整式),不等号的方向不变
不等式的性质2:不等式的两边乘以(或除以)同一个正数,不等号的方向不变
不等式的性质3:不等式的两边乘以(或除以)同一个负数, 不等号的方向改变
2.(1).定起点,确定空心圆圈或实心圆点
有等号的画实心圆点,
无等号的画空心圆圈;
(2).确定方向
大于向右画,小于向左画.
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为X吨,请用不等式分别表示上面两位同学所谈话的内容:
②
①
看,这头大象好大呀,体重肯定大于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
问题情境
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量 至少是两个。
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
探究新知1
判断下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
小试身手
对应练习1
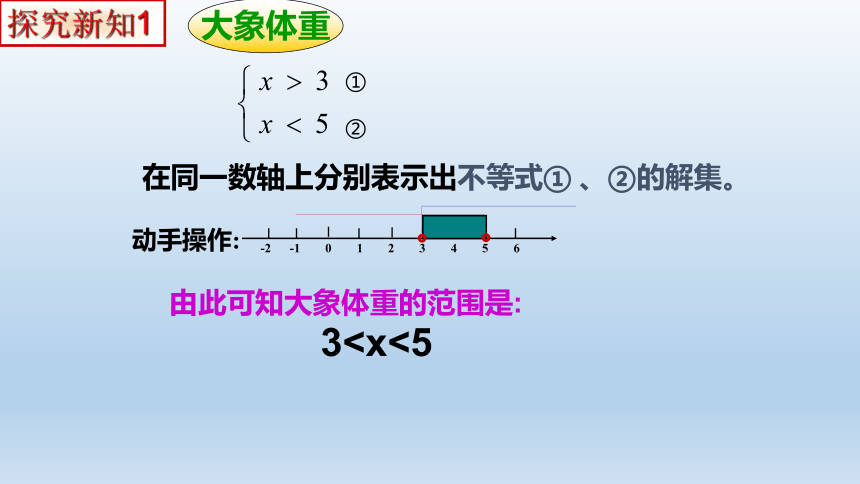
②
①
动手操作:
大象体重
-2 -1 0 1 2 3 4 5 6
在同一数轴上分别表示出不等式① 、②的解集。
由此可知大象体重的范围是:
3。
。
探究新知1
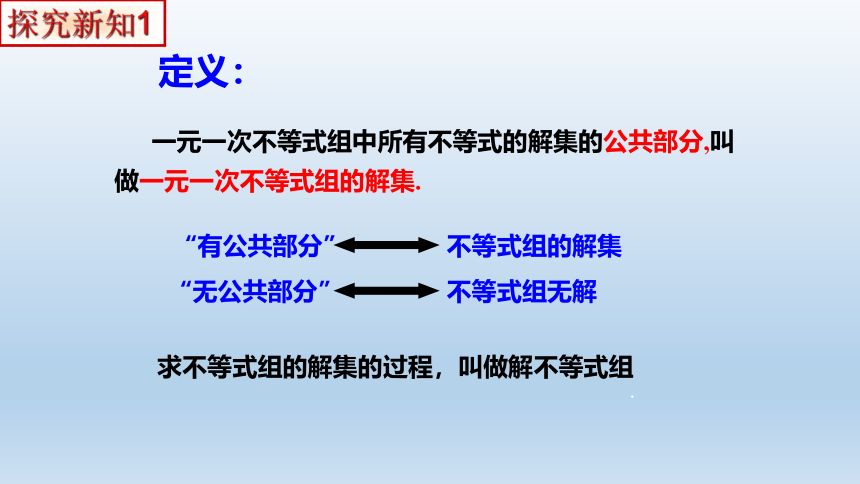
一元一次不等式组中所有不等式的解集的公共部分,叫做一元一次不等式组的解集.
“有公共部分”
不等式组的解集
“无公共部分”
不等式组无解
求不等式组的解集的过程,叫做解不等式组
定义:
探究新知1
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中x的取值范围呢?
不等式组中各不等式解集的公共部分,
就是不等式组中x的取值范围
探究新知2
0
-6
0
1
解:解不等式①,得 x>-6
解不等式②,得 x>1
所以,不等式组的解集是x>1
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
探究新知2
在数轴上表示不等式①,②的解集
这两个不等式解集的公共部分是x>1
例1:
解一元一次不等式组的“四步曲”
2.画数轴表示各个解集;
1.解出组成不等式组中各个不等式;
4.写出这个不等式组的解集。
探究新知2
3.找出几个解集的公共部分;
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
同大取大
一元一次不等式组的解集的确定规律(1)
探究新知3
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
同小取小
一元一次不等式组的解集的确定规律(2)
探究新知3
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律(3)
探究新知3
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:不等式组无解.
解:不等式组无解.
解:不等式组无解.
解:不等式组无解.
大大小小题无解
一元一次不等式组的解集的确定规律(4)
探究新知3
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小题无解)
一元一次不等式组的解集的确定规律
探究新知3
1.比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小题无解。
x>2
x>-2
x<3
x<-4
3-1无解
无解
-2≤x<1
x≤-2
x<-2
对应练习3
例题解析
例2 解不等式组
解不等式②,得 x>2
所以,这个不等式组无解
在数轴上表示不等式①,②的解集
这两个不等式解集没有公共部分
解:解不等式①,得 x<1
0
1
2
①
②
2.画数轴表示各个解集;
1.解出组成不等式组中各个不等式;
4.写出这个不等式组的解集。
3.找出几个解集的公共部分;
能力提升
1.已知4a+5和2a-4的值都是正数,求a的取值范围.
解不等式②,得 a>2
所以,不等式组的解集是a>2,即a的取值范围是a>2.
在数轴上表示不等式①,②的解集
这两个不等式解集的公共部分是a>2
4a+5>0 ①
2a-4>0 ②
解:根据题意得:
解不等式①,得 a>
0
1
2
2. 已知关于x的不等式组 的解集是x>-1.
求m的值.
由题意得不等式组的解集是x>-1
且m+2>m-1
同大取大
所以,不等式组的解集是
解:因为
所以m+2=-1,m=-3
能力提升
-2≤a<-1
[解析] 由题意可知,不等式的解集是a因为不等式组恰有3个整数解,所以这3个整数解为-1,0,1,
能力提升
0
1
2
-1
-2
a
0
1
2
-1
-2
a
0
1
2
-1
-2
a
a=-1
×
-2√
a=-2
√
所以a的取值范围是-2≤a<-1.
学习了本节课你有哪些 收获?
课堂小结
3.求不等式组的解集的过程,叫做解不等式组.
5.确定一元一次不等式组解集的方法:
(1)利用数轴找几个解集的公共部分:
(2)利用规律: 同大取大,同小取小;大小小大中间找,大大小小题无解。
1.把两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
2.一元一次不等式组中所有不等式的解集的公共部分,叫做一元一次不等式组的解集。
课堂小结
4.解一元一次不等式组的“四步曲”:解、画、找、写.
谢谢,再见!
10.5 一元一次不等式组
七年级数学·下 [冀教]
第十章 一元一次不等式和
一元一次不等式组
1.理解一元一次不等式组的概念,以及解集的意义.
2.掌握一元一次不等式组的解法,并能利用数轴确定其解集.
学习目标
3.会求一元一次不等式组的特殊解.
4.对含字母的一元一次不等式组,会根据解集求字母的取值范围.
1.不等式-X>-2的解是( )
A. X>2 B. X>-2
C. X<2 D. X<-2
C
2.如图所示,数轴表示
的是( )不等式的解集
A. X>-1 B. X<-1
C. X≤-1 D. X≥-1
-2 -1 0 1
D
知识回顾
1.掌握不等式的三条基本性质
不等式的性质1:不等式的两边加上(或减去)同一个数(或同一个整式),不等号的方向不变
不等式的性质2:不等式的两边乘以(或除以)同一个正数,不等号的方向不变
不等式的性质3:不等式的两边乘以(或除以)同一个负数, 不等号的方向改变
2.(1).定起点,确定空心圆圈或实心圆点
有等号的画实心圆点,
无等号的画空心圆圈;
(2).确定方向
大于向右画,小于向左画.
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为X吨,请用不等式分别表示上面两位同学所谈话的内容:
②
①
看,这头大象好大呀,体重肯定大于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
问题情境
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量 至少是两个。
类似于方程组,把这两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
探究新知1
判断下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
小试身手
对应练习1
②
①
动手操作:
大象体重
-2 -1 0 1 2 3 4 5 6
在同一数轴上分别表示出不等式① 、②的解集。
由此可知大象体重的范围是:
3
。
探究新知1
一元一次不等式组中所有不等式的解集的公共部分,叫做一元一次不等式组的解集.
“有公共部分”
不等式组的解集
“无公共部分”
不等式组无解
求不等式组的解集的过程,叫做解不等式组
定义:
探究新知1
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中x的取值范围呢?
不等式组中各不等式解集的公共部分,
就是不等式组中x的取值范围
探究新知2
0
-6
0
1
解:解不等式①,得 x>-6
解不等式②,得 x>1
所以,不等式组的解集是x>1
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
探究新知2
在数轴上表示不等式①,②的解集
这两个不等式解集的公共部分是x>1
例1:
解一元一次不等式组的“四步曲”
2.画数轴表示各个解集;
1.解出组成不等式组中各个不等式;
4.写出这个不等式组的解集。
探究新知2
3.找出几个解集的公共部分;
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
同大取大
一元一次不等式组的解集的确定规律(1)
探究新知3
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
同小取小
一元一次不等式组的解集的确定规律(2)
探究新知3
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
解:不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律(3)
探究新知3
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:不等式组无解.
解:不等式组无解.
解:不等式组无解.
解:不等式组无解.
大大小小题无解
一元一次不等式组的解集的确定规律(4)
探究新知3
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
(若当 a<b时 )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小题无解)
一元一次不等式组的解集的确定规律
探究新知3
1.比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小题无解。
x>2
x>-2
x<3
x<-4
3
无解
-2≤x<1
x≤-2
x<-2
对应练习3
例题解析
例2 解不等式组
解不等式②,得 x>2
所以,这个不等式组无解
在数轴上表示不等式①,②的解集
这两个不等式解集没有公共部分
解:解不等式①,得 x<1
0
1
2
①
②
2.画数轴表示各个解集;
1.解出组成不等式组中各个不等式;
4.写出这个不等式组的解集。
3.找出几个解集的公共部分;
能力提升
1.已知4a+5和2a-4的值都是正数,求a的取值范围.
解不等式②,得 a>2
所以,不等式组的解集是a>2,即a的取值范围是a>2.
在数轴上表示不等式①,②的解集
这两个不等式解集的公共部分是a>2
4a+5>0 ①
2a-4>0 ②
解:根据题意得:
解不等式①,得 a>
0
1
2
2. 已知关于x的不等式组 的解集是x>-1.
求m的值.
由题意得不等式组的解集是x>-1
且m+2>m-1
同大取大
所以,不等式组的解集是
解:因为
所以m+2=-1,m=-3
能力提升
-2≤a<-1
[解析] 由题意可知,不等式的解集是a
能力提升
0
1
2
-1
-2
a
0
1
2
-1
-2
a
0
1
2
-1
-2
a
a=-1
×
-2
a=-2
√
所以a的取值范围是-2≤a<-1.
学习了本节课你有哪些 收获?
课堂小结
3.求不等式组的解集的过程,叫做解不等式组.
5.确定一元一次不等式组解集的方法:
(1)利用数轴找几个解集的公共部分:
(2)利用规律: 同大取大,同小取小;大小小大中间找,大大小小题无解。
1.把两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组。
2.一元一次不等式组中所有不等式的解集的公共部分,叫做一元一次不等式组的解集。
课堂小结
4.解一元一次不等式组的“四步曲”:解、画、找、写.
谢谢,再见!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
