中考复习专题(七): 一次函数(知识点精讲+热点题型+名师押题精讲)
文档属性
| 名称 | 中考复习专题(七): 一次函数(知识点精讲+热点题型+名师押题精讲) |  | |
| 格式 | zip | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 17:13:36 | ||
图片预览




文档简介
第一部分 知识点精讲
一 次 函 数
课标要求:
了解一次函数有关概念,正反比例函数的概念。
②了解一次函数的性质,了解函数图像经过的象限。
③了解一次函数的图像与k、b的符号关系。
④了解一次函数的增减性。
⑤一次函数表达式的求法。
⑥会求一次函数y=kx+b;y=k/x中,k与b的取值范围。
⑦一次函数与一元一次方程(组)、一元一次不等式的关系。
⑧一次函数的应用。
⑨用一次函数求量值。
考点清单:
①一次函数:形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
正比例函数:当b=0时,一次函数y=kx+b就变为y=kx(k为常数,k≠0)这时我们称y是x的正比例函数。
③一次函数y=kx+b的图像是一条经过点(0,b)和点(-b/k,0)的直线;正比例函数y=kx的图像是一条经过点(0,0)的直线。
在一次函数y=kx+b中,当k﹥0,y的值随x值的增大而增大;当k﹤0时,y的值随x值的增大而增大而减小。
⑤在一次函数y=kx+b中,当k﹥0时,其图象必经过第一、三象限;当k﹤0时,其图象必经过第二、四象限。
一次函数y=kx+b的图象与k、b的符号关系
⑴k﹥0, b﹤0时,图象经过第一、二、三象限。
⑵k﹥0, b﹤0时,图象经过第一、三、四象限。
⑶k﹤0 ,b﹥0时,图象经过第一、二、四象限。
⑷k﹤0 ,b﹥0时,图象经过第二、三、四象限。
反比例函数的概念及性质。
⑴反比例函数:形如y=k/x(k是常数,k≠0)的函数称之为反比例函数。
⑵反比例函数的图像是双曲线,具有如下性质:
k﹥0,双曲线位于第一三象限内,在每个象限内y随x增大而减小。与x轴y轴无交点。
k﹤0,双曲线位于第二四象限内,在每个象限内y随x增大而增大。与x轴y轴无交点。
A部分:考试指南
历年真题
例1、已知正比例函数y=-kx和一次函数y=kx-2(x为自变量),它们在同一坐标系内的图象大致是( )
y y y y
x x x x
B、 C、 D、
【答案】A
【考点】一次函数的图象;正比例函数的图象.
【分析】分k大于0和k小于0两种情况讨论.k>0时,分别画出两函数图象;k<0时分别画出两函数图象;与选项中图象对照.符合题意的即为正确答案.解答:解:分两种情况:(1)当k>0时,正比例函数y=-kx的图象过原点、第一、三象限,一次函数y=kx-2的图象经过第一、三、四象限,选项A符合;
(2)当k<0时,正比例函数y=-kx的图象过原点、第二、四象限,一次函数y=kx-2的图象经过第二、三、四象限,无选项符合.
故选A.点评:一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
例2、函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的【 度002】
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
【答案】D。
【考点】反比例函数的性质。
【分析】将(2,-2)代入y=(k≠0)得k=-4,根据反比例函数的性质,函数的图象在平面直角坐标系中的第二、四象限。故选D。
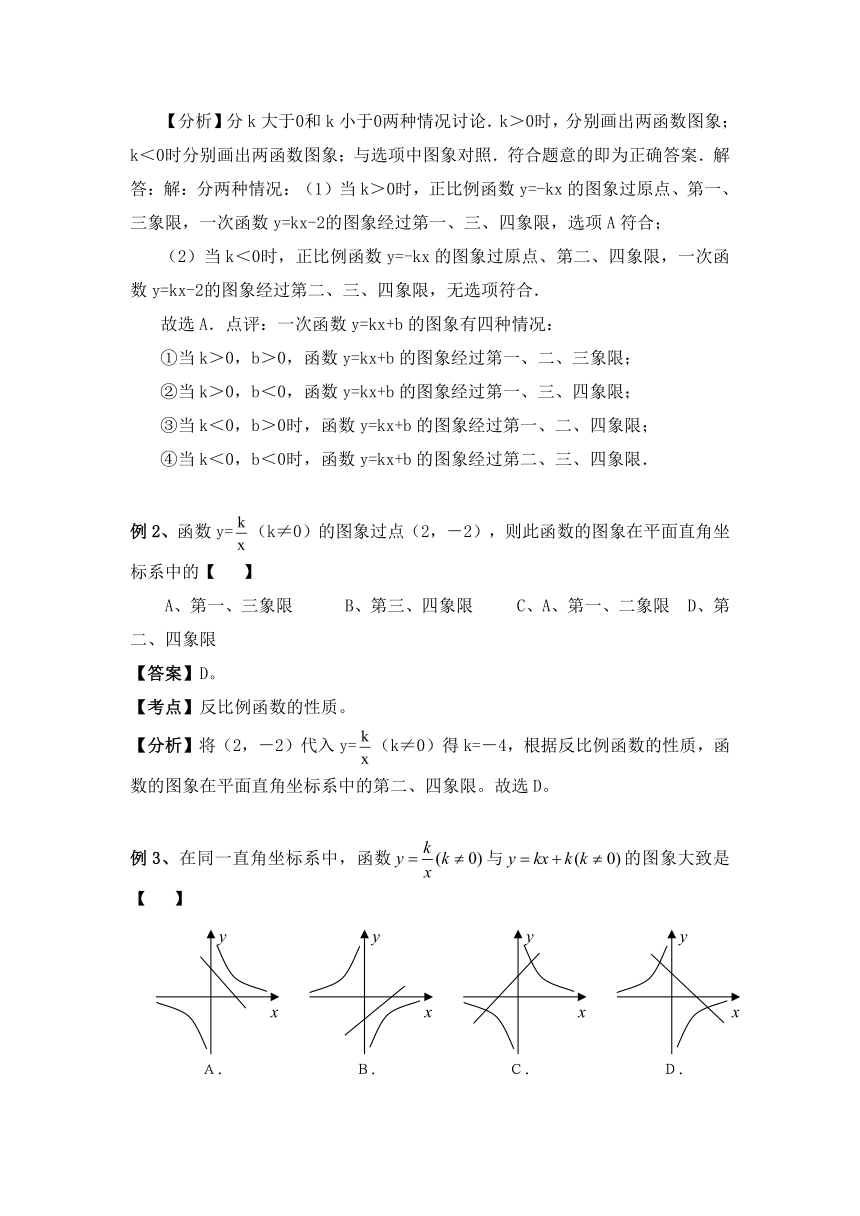
例3、在同一直角坐标系中,函数与的图象大致是【 度002】
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】若>0,反比例函数的图象经过一、三象限,一次函数的图象经过一、二、三象限,答案C符合条件;若<0,反比例函数的图象经过二、四象限,一次函数的图象经过二、三、四象限。
例4、函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的【 度002】
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
【答案】D。
【考点】反比例函数的性质。
【分析】将(2,-2)代入y=(k≠0)得k=-4,根据反比例函数的性质,函数的图象在平面直角坐标系中的第二、四象限。故选D。
例5、函数的图象如图所示,那么函数的图象大致是【 度002】
A B C D
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】∵反比例函数的图象位于第二、四象限,∴<0。
∵<0,∴函数的图象过二、四象限.
又∵->0,∴函数的图象与y轴相交于正半轴。
例6、在同一直角坐标系中,函数与的图象大致是【 度002】
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】若>0,反比例函数的图象经过一、三象限,一次函数的图象经过一、二、三象限,答案C符合条件;若<0,反比例函数的图象经过二、四象限,一次函数的图象经过二、三、四象限,答案中没有符合条件的结果。故选C。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律一:(点击展开)
考查一次函数数概念有关的问题,如:一次函数的判断,一次函数图像经过的象限,反比例函数图像经过的象限,一次函数和反比例函数的图像经过的象限。
例7、.如图,反比例函数的图象与直线的交点为A,B,过点A作轴的平行线与过点B作轴的平行线相交于点C,则△ABC的面积为【 度002】
A.8 B.6 C.4 D.2
【答案】A。
【考点】反比例函数系数的几何意义。
【分析】双曲线上任意一点引轴、轴垂线,所得矩形面积为||,根据反比例函数的中心对称特点可知△ABC的是面积2||=2×4=8。故选A。
例8、在反比例函数的图象的每一条曲线上,都随的增大而增大,则的值可以是【 度002】
A .-1 B .0 C . 1 D .2
【答案】D。
【考点】反比例函数的性质。
【分析】由反比例函数的图象的每一条曲线上,都随的增大而增大,得因此的值可以是2。故选D。
例9、反比例函数y=在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是【 度002】
A、1 B、2 C、4 D、
【答案】B。
【考点】反比例函数系数k的几何意义。
【分析】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S= |k|即可求得k的值:
∵点M是反比例函数y=图象上一点,∴S△MOP= |k|=1。
又∵k>0,则k=2。故选B。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律二:(点击展开)以上三题主要考查反比例函数K值的意义及它的综合运用。
例10、如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为,则tanA的值是 ▲ .
【答案】。
【考点】三角形的内心,等腰直角三角形的性质,勾股定理,一次函数,锐角三角函数。
【分析】过A作AE⊥X轴于E,AC交Y轴于D,AB交X轴于F。
∵点C的坐标为(2,0),点B的坐标为(0,2),
∴∠OCB=∠OBC=45 ,BC=。
又∵△ABC的内心在y轴上,∴∠OBF=∠OBC=45 。
∴∠ABC=90 ,BF=BC=,CF=4,EF=EA。
又∵直线AC的解析式为,∴OD:OC=1:2。
∵A点在直线AC上,∴AE:EC=1:2,即AE:(EF+CF)=AE:(AE+4)=1:2。
解之,EF=AE=4,∴FA=。∴AB=BF+FA=。
∴在Rt △ABC中,tanA= 。
例11、已知一元二次方程2x2-3x-6=0有两个实数根x1、x2,直线l经过点A(x1+x2,0)、B(0,x1x2),则直线l的解析式为【 度002】
A、y=2x-3 B、y=2x+3 C、y=-2x-3 D、y=-2x+3
【答案】A。
【考点】一元二次方程根与系数的关系,待定系数法求一次函数解析式。
【分析】根据一元二次方程根与系数的关系,求出A,B的坐标,代入直线的解析式,求出k,b的值,从而确定直线的解析式:
由题意知,x1+x2=,x1 x2=-3,∴A(,0),B(0,-3)。
设直线l的解析式为:y=kx+b,把点A,点B的坐标代入,解得,k=2,b=-3,
∴直线l的解析式为:y=2x-3。故选A。
例12、如图,点P(3a,a)是反比例函y=(k>0)与⊙O
的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 度002】
A.y= B.y= C.y= D.y=
【答案】D。
【考点】反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。
【分析】根据反比例函数和圆的中心对称性,图中阴影部分的面积实际上是圆的面积。由勾股定理,可得圆的
半径为。因此,由图中阴影部分的面积为10π可得,解得a=2(因果点P在第一象限,
a>0,负数舍去)。∴点P(6,2)。代入y=,得k=12。则反比例函数的解析式为y=。故选D。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律三:(点击展开)
涉及到生活中与一次函数数相关的内容,解析式的求法,数学其它知识点与一次函数知识点的综合考查。
第二部分 热点题型精讲
热点题型:
第一类:一次函数概念 第二类:一次函数的图像及性质
第三类:一次函数K值与b的关系 第四类:求解析式及其综合运用
第五类:一次函数与生活知识的应用
第一类:一次函数概念
1、下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A、1 B、2 C、3 D、4
考点:一次函数的定义.
分析:根据一次函数的定义条件进行逐一分析即可.
解答:解:①y=x是一次函数;
②y=是一次函数;
③y=自变量次数不为1,故不是一次函数;
④y=2x+1是一次函数.
故选C.
点评:本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
2、在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用关系式y=35x+20表示,这个关系式符合的数学模型是( )
A、正比例函数 B、反比例函数 C、二次函数 D、一次函数
考点:一次函数的定义.
分析:根据一次函数的定义解答即可.
解答:解:∵关系式y=35x+20符合一次函数的形式,
∴这个关系式符合的数学模型是一次函数.
故选D.
点评:本题考查一次函数的定义,即形如y=kx+b,(k≠0,k、b为常数)的函数叫一次函数.
第二类:一次函数的图像及性质
3、函数的图象如图所示,那么函数的图象大致是【 度002】
A B C D
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】∵反比例函数的图象位于第二、四象限,∴<0。
∵<0,∴函数的图象过二、四象限.
又∵->0,∴函数的图象与y轴相交于正半轴。
第三类:一次函数K值与b的关系
4、一次函数y=(k-2)x+3的图象如图所示,则k的取值范围是( )
A、k>2 B、k<2 C、k>3 D、k<3
考点:一次函数图象与系数的关系.
专题:探究型.
分析:先根据一次函数的图象得到关于k的不等式,求出k的取值范围即可.
解答:解:一次函数的图象过二、四象限可知,k-2<0,
解得k<2.
故选B.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0时,函数的图象过二、四象限.
5、直线y=3x+b 与两坐标轴围成的三角形面积为6,求与y轴的交点坐标( )
A、(0,2) B、(0,-2)(0,2) C、(0,6) D、(0,6)、(0,-6)
考点:一次函数的图象;点的坐标;一次函数图象上点的坐标特征.
专题:探究型.
分析:先令x=0用b表示出y的值,再令y=0得出x的值,根据三角形的面积公式及绝对值的性质求出b的值即可.
解答:解:令x=0,则y=b,令y=0,则x=-6,
∵直线y=3x+b 与两坐标轴围成的三角形面积为6,
∴|b|×|-1|=6,即b=6,
∴b=±6,
∴y轴的交点坐标为(0,6),(0,-6).
故选D.
点评:本题考查的是一次函数的图象及一次函数图象上点的坐标特点、三角形的面积公式,熟知一次函数的图象是直线是解答此题的关键.
第四类:求解析式及其综合运用
6、在平面直角坐标系中,把直线y=x向左平移一个单位长度后,其直线解析式为( )
A、y=x+1 B、y=x-1 C、y=x D、y=x-2
考点:一次函数图象与几何变换.
专题:探究型.
分析:根据“左加右减”的原则进行解答即可.
解答:解:由“左加右减”的原则可知,在平面直角坐标系中,把直线y=x向左平移一个单位长度后,
其直线解析式为y=x+1.
故选A.
点评:本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
7、如图,点P(3a,a)是反比例函y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 度002】
A.y= B.y= C.y= D.y=
考点:反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。
专题:探究型
分析:根据反比例函数和圆的中心对称性,图中阴影部分的面积实际上是圆的面积。
解答:由勾股定理,可得圆的半径为。因此,由图中阴影部分的面积为10π可得,解得a=2(因果点P在第一象限)
故选D.
点评:本题考查反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。熟练运用勾股定理是解此题的关键。
8、以下是2002年3月12日《南国早报》刊登的南宁市自来水价格调整表:
南宁市自来水价格调整表(部分)单位:元/立方米
用水类别 现行水价 拟调整水价一、居民生活用水 0.72
1、一户一表
第一阶梯:月用水量0~30立方米/户 0.82
第二阶梯:月用水量超过30立方米/户部分 1.23
则调整水价后某户居民月用水量x(立万米)与应交水费y(元)的函数图象是( )
A、 B 、 C、 D、
考点:一次函数的图象;一次函数的应用.
分析:根据题意:函数的图象为分段函数,两段均为一次函数,且当x>50时,收费更高,故直线倾斜程度变大,据此作出选择.
解答:解:根据图中信息,列出函数解析式得:①y=0.82x(0<x<30);②y=1.23x(30<x<50).故选C.
点评:本题要求学生根据题意,结合实际情况,判断函数的图象.
第五类:一次函数与生活知识的应用
9、直线y=-x+m与直线y=x+2相交于y轴上的点C,与x轴分别交于点A、B。
(1)求A、B、C三点的坐标;(3分)
(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(4分)
(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离(可用含θ的三角函数式表示)。(5分)
【答案】解:(1)直线y= x+2中令x=0,得y=2,
∴C点的坐标为(0,2)。
把C(0,2)代入直线y=-x+m,得m=2,
∴直线y=-x+m解析式是y=-x+2。
令y=0,得x=2,则A点的坐标是(2,0),
在y= x+2中令y=0,得x=,则B的坐标是(,0)。
(2)根据A、B、C的坐标得到OC=2,OA=2,OB=,根据锐角三角函数定义,得tan∠ABC=,∴∠ABC=30°。
又AC=。
连接AE,CE,过点E作EF⊥AB于点F,则∠AEC=60°,
∴△ACE是等边三角形,边长是。
又在Rt△EAF中,AE=,AF=AB=,
∴EF=。
又OF=OA+AF=。
∴点E的坐标为(,),半径是。
(3)分两种情况:
(I)当点P在⊙E外时,如图,连接AN,连接ME并延长交⊙E于另一点Q,连接NQ,则△NQM是直角三角形。
∵∠MQN=∠MAN=∠ANC-∠P=∠ABC-∠P=30°-θ,
∴在Rt△NQM中,MN=QMsin∠MQN,
即MN=sin(30°-θ)。
(II)当点P在⊙E内时,如图,连接AN,连接ME并延长交⊙E于另一点Q,连接NQ,则△NQM是直角三角形。
∵∠ACB=∠BCO-∠ACO=60°-45°=15°。
∴∠MQN=∠MAN=∠APB-∠ANB=∠APB-∠ACB =θ-15°。
∴在Rt△NQM中,MN=QMsin∠MQN,
即MN=sin(θ-15°)。
【考点】一次函数综合题,直线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,勾股定理,等边三角形的判定和性质,圆周角定理,弦径定理,三角形外角定理。
【分析】(1)直线y= x+2与y轴的交点可以求出,把这点的坐标就可以求出直线y=-x+m的解析式,两个函数与x轴的交点就可以求出。
(2)根据三角函数可以求出角的度数。由OC、OA、OB的长度,根据勾股定理、等边三角形的判定和性质、弦径定理可求出点E的坐标和⊙E的半径。
(3)分点P在⊙E外和点P在⊙E内两种情况讨论即可。
点评:本题必须熟练运用直线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,勾股定理,等边三角形的判定和性质,圆周角定理,弦径定理,三角形外角定理。
第三部分 名师押题
名师押题
1、下列函数①y=πx,②y=2x-1,③,④y=2-1-3x,⑤y=x2-1中,是一次函数的有( )
A、4个 B、3个 C、2个 D、1个
考点:一次函数的定义.分析:根据一次函数的定义条件进行逐一分析即可.
解答:解:①y=πx是一次函数;
②y=2x-1是一次函数;
③y=πx ,自变量次数不为1,不是一次函数;
④y=2-1-3x是一次函数;
⑤y=x2-1,自变量次数不为1,不是一次函数.
故选B.点评:本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
2.已知正比例函数y=-kx和一次函数y=kx-2(x为自变量),它们在同一坐标系内的图象大致是( )
A、 B、 C、 D、
考点:一次函数的图象;正比例函数的图象.
分析:分k大于0和k小于0两种情况讨论.k>0时,分别画出两函数图象;k<0时分别画出两函数图象;与选项中图象对照.符合题意的即为正确答案.
解答:解:分两种情况:(1)当k>0时,正比例函数y=-kx的图象过原点、第一、三象限,一次函数y=kx-2的图象经过第一、三、四象限,选项A符合;
(2)当k<0时,正比例函数y=-kx的图象过原点、第二、四象限,一次函数y=kx-2的图象经过第二、三、四象限,无选项符合.
故选A.
点评:一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
3.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
A、x>0 B、x<0 C、x>2 D、x<2
考点:一次函数的图象.
专题:数形结合.
分析:根据函数图象可知,此函数为减函数,图象与x轴的交点坐标为(2,0),由此可得出答案.
解答:解:根据图象和数据可知,当y<0即直线在x轴下方时,x的取值范围是x>2.
故选C.
点评:本题考查一次函数的图象,考查学生的分析能力和读图能力.
4.在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用关系式y=35x+20表示,这个关系式符合的数学模型是( )
A、正比例函数 B、反比例函数 C、二次函数 D、一次函数
考点:一次函数的定义.
分析:根据一次函数的定义解答即可.
解答:解:∵关系式y=35x+20符合一次函数的形式,
∴这个关系式符合的数学模型是一次函数.
故选D.
点评:本题考查一次函数的定义,即形如y=kx+b,(k≠0,k、b为常数)的函数叫一次函数.
5.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是( )
A、m<0 B、m>0 C、m<2 D、m>2
考点:一次函数的性质.
专题:探究型.
分析:根据一次函数的性质列出关于m的不等式,求出m的取值范围即可.
解答:解:∵一次函数y=(2-m)x-2的函数值y随x的增大而减小,
∴2-m<0,
∴m>2.
故选D.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0时,y随x的增大而减小.
6. P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,则下列判断正确的是( )
A、y1>y2 B、y1<y2 C、当x1<x2时,y1>y2 D、当x1<x2时,y1<y2
考点:正比例函数的性质.
分析:根据正比例函数图象的性质可知.
解答:解:根据k<0,得y随x的增大而减小.
故选C.
点评:了解正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.
7.已知一次函数y=kx+b的图象经过第一、二、三象限,则b的值可以是( )
A、-2 B、-1 C、0 D、2
考点:一次函数图象与系数的关系.
专题:探究型.
分析:根据一次函数的图象经过第一、二、三象限判断出b的符号,再找出符合条件的b的可能值即可.解答:解:∵一次函数的图象经过第一、二、三象限,
∴b>0,
∴四个选项中只有2符合条件.
故选D.
点评:本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当b<0时,函数图象与y轴相交于负半轴.
8.如图的坐标平面上,有一条通过点(-3,-2)的直线L.若四点(-2,a)、(0,b)、(c,0)、(d,-1)在L上,则下列数值的判断,何者正确( )
A、a=3 B、b>-2 C、c<-3 D、d=2
考点:一次函数图象上点的坐标特征.
专题:数形结合.
分析:根据函数的图象可判断出函数的增减性,从而结合选项即可判断各选项正确与否.
解答:解:由题意得:此函数为减函数,
A、-2>-3,故a<-2,故本选项错误;
B、-3<0,故-2>b,故本选项错误;
C、0>-2,故c<-3,故本选项正确;
D、-1>-2,故b<-3,故本选项错误.
故选C.
点评:本题考查一次函数图象上点的坐标特征,解答本题的关键是掌握函数的增减性,另外本题还可以利用特殊值设出符合题意的函数解析式,然后代入判断.
9.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(a,b),且2a+b=6,则直线AB的解析式是( )
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+6
考点:一次函数图象与几何变换.
专题:数形结合.
分析:平移时k的值不变,只有b发生变化.再把相应的点代入即可.
解答:解:原直线的k=-2,向上平移后得到了新直线,那么新直线的k=-2.
∵直线AB经过点(a,b),且2a+b=6.
∴直线AB经过点(a,6-2a).
可设新直线的解析式为y=-2x+b1,
∴6-2a=-2a+b1,
则b1=6,
∴直线AB的解析式是y=-2x+6.
故选D.
点评:求直线平移后的解析式时要注意平移k值不变.
10.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程是2x+b=0的解是x=2。
考点:一次函数与一元一次方程.
专题:计算题.
分析:根据直线y=2x+b与x轴的交点坐标是(2,0),求得b,再把b代入方程2x+b=0,求解即可.
解答:解:把(2,0)代入y=2x+b,
得:b=-4,把b=-4代入方程2x+b=0,
得:x=2.
故填2.
点评:考查了一次函数与坐标轴的交点坐标问题,还考查了方程解的定义.
11、目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
A、y=0.05x B、y=5xC、y=100x D、y=0.05x+100
考点:根据实际问题列一次函数关系式.
分析:每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
解答:解:y=100×0.05x,
即y=5x.
故选B.
点评:本题主要考查了根据实际问题列一次函数解析式,正确表示出一分钟滴的水的体积是解题的关键.
12.如图,函数y=mx-4m的图象分别交x轴、y轴于点N、M,线段MN上两点A、B在x轴上的垂足分别为A1、B1,若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( )
A、S1>S2 B、S1=S2 C、S1<S2 D、不确定的
考点:一次函数综合题.
分析:设A(a,ma-4m),B(b,mb-4m)表示出S1和S2,然后让两式相减即可比较出大小.
解答:解:设A(a,ma-4m),B(b,mb-4m),则:
S1=1 2a×(ma-4m),S2=1/2b(mb-4m)
S1-S2=1 2(ma2-mb2)-1 24m(a-b)=(a-b){1 2m(a+b)-1 2.4m}
又∵OA1+OB1>4
∴1 2m(a+b)-1 24m=1/2m(a+b-4)<0
∴S1-S2>0
故选A.
点评:本题考查三角形和坐标系的结合,属于比较好的题.同学们要注意掌握这类数形结合题目的解答.
A.
B.
C.
D.
A.
B.
C.
D.
A
O
B
C
一 次 函 数
课标要求:
了解一次函数有关概念,正反比例函数的概念。
②了解一次函数的性质,了解函数图像经过的象限。
③了解一次函数的图像与k、b的符号关系。
④了解一次函数的增减性。
⑤一次函数表达式的求法。
⑥会求一次函数y=kx+b;y=k/x中,k与b的取值范围。
⑦一次函数与一元一次方程(组)、一元一次不等式的关系。
⑧一次函数的应用。
⑨用一次函数求量值。
考点清单:
①一次函数:形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
正比例函数:当b=0时,一次函数y=kx+b就变为y=kx(k为常数,k≠0)这时我们称y是x的正比例函数。
③一次函数y=kx+b的图像是一条经过点(0,b)和点(-b/k,0)的直线;正比例函数y=kx的图像是一条经过点(0,0)的直线。
在一次函数y=kx+b中,当k﹥0,y的值随x值的增大而增大;当k﹤0时,y的值随x值的增大而增大而减小。
⑤在一次函数y=kx+b中,当k﹥0时,其图象必经过第一、三象限;当k﹤0时,其图象必经过第二、四象限。
一次函数y=kx+b的图象与k、b的符号关系
⑴k﹥0, b﹤0时,图象经过第一、二、三象限。
⑵k﹥0, b﹤0时,图象经过第一、三、四象限。
⑶k﹤0 ,b﹥0时,图象经过第一、二、四象限。
⑷k﹤0 ,b﹥0时,图象经过第二、三、四象限。
反比例函数的概念及性质。
⑴反比例函数:形如y=k/x(k是常数,k≠0)的函数称之为反比例函数。
⑵反比例函数的图像是双曲线,具有如下性质:
k﹥0,双曲线位于第一三象限内,在每个象限内y随x增大而减小。与x轴y轴无交点。
k﹤0,双曲线位于第二四象限内,在每个象限内y随x增大而增大。与x轴y轴无交点。
A部分:考试指南
历年真题
例1、已知正比例函数y=-kx和一次函数y=kx-2(x为自变量),它们在同一坐标系内的图象大致是( )
y y y y
x x x x
B、 C、 D、
【答案】A
【考点】一次函数的图象;正比例函数的图象.
【分析】分k大于0和k小于0两种情况讨论.k>0时,分别画出两函数图象;k<0时分别画出两函数图象;与选项中图象对照.符合题意的即为正确答案.解答:解:分两种情况:(1)当k>0时,正比例函数y=-kx的图象过原点、第一、三象限,一次函数y=kx-2的图象经过第一、三、四象限,选项A符合;
(2)当k<0时,正比例函数y=-kx的图象过原点、第二、四象限,一次函数y=kx-2的图象经过第二、三、四象限,无选项符合.
故选A.点评:一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
例2、函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的【 度002】
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
【答案】D。
【考点】反比例函数的性质。
【分析】将(2,-2)代入y=(k≠0)得k=-4,根据反比例函数的性质,函数的图象在平面直角坐标系中的第二、四象限。故选D。
例3、在同一直角坐标系中,函数与的图象大致是【 度002】
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】若>0,反比例函数的图象经过一、三象限,一次函数的图象经过一、二、三象限,答案C符合条件;若<0,反比例函数的图象经过二、四象限,一次函数的图象经过二、三、四象限。
例4、函数y=(k≠0)的图象过点(2,-2),则此函数的图象在平面直角坐标系中的【 度002】
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
【答案】D。
【考点】反比例函数的性质。
【分析】将(2,-2)代入y=(k≠0)得k=-4,根据反比例函数的性质,函数的图象在平面直角坐标系中的第二、四象限。故选D。
例5、函数的图象如图所示,那么函数的图象大致是【 度002】
A B C D
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】∵反比例函数的图象位于第二、四象限,∴<0。
∵<0,∴函数的图象过二、四象限.
又∵->0,∴函数的图象与y轴相交于正半轴。
例6、在同一直角坐标系中,函数与的图象大致是【 度002】
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】若>0,反比例函数的图象经过一、三象限,一次函数的图象经过一、二、三象限,答案C符合条件;若<0,反比例函数的图象经过二、四象限,一次函数的图象经过二、三、四象限,答案中没有符合条件的结果。故选C。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律一:(点击展开)
考查一次函数数概念有关的问题,如:一次函数的判断,一次函数图像经过的象限,反比例函数图像经过的象限,一次函数和反比例函数的图像经过的象限。
例7、.如图,反比例函数的图象与直线的交点为A,B,过点A作轴的平行线与过点B作轴的平行线相交于点C,则△ABC的面积为【 度002】
A.8 B.6 C.4 D.2
【答案】A。
【考点】反比例函数系数的几何意义。
【分析】双曲线上任意一点引轴、轴垂线,所得矩形面积为||,根据反比例函数的中心对称特点可知△ABC的是面积2||=2×4=8。故选A。
例8、在反比例函数的图象的每一条曲线上,都随的增大而增大,则的值可以是【 度002】
A .-1 B .0 C . 1 D .2
【答案】D。
【考点】反比例函数的性质。
【分析】由反比例函数的图象的每一条曲线上,都随的增大而增大,得因此的值可以是2。故选D。
例9、反比例函数y=在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是【 度002】
A、1 B、2 C、4 D、
【答案】B。
【考点】反比例函数系数k的几何意义。
【分析】根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系S= |k|即可求得k的值:
∵点M是反比例函数y=图象上一点,∴S△MOP= |k|=1。
又∵k>0,则k=2。故选B。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律二:(点击展开)以上三题主要考查反比例函数K值的意义及它的综合运用。
例10、如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为,则tanA的值是 ▲ .
【答案】。
【考点】三角形的内心,等腰直角三角形的性质,勾股定理,一次函数,锐角三角函数。
【分析】过A作AE⊥X轴于E,AC交Y轴于D,AB交X轴于F。
∵点C的坐标为(2,0),点B的坐标为(0,2),
∴∠OCB=∠OBC=45 ,BC=。
又∵△ABC的内心在y轴上,∴∠OBF=∠OBC=45 。
∴∠ABC=90 ,BF=BC=,CF=4,EF=EA。
又∵直线AC的解析式为,∴OD:OC=1:2。
∵A点在直线AC上,∴AE:EC=1:2,即AE:(EF+CF)=AE:(AE+4)=1:2。
解之,EF=AE=4,∴FA=。∴AB=BF+FA=。
∴在Rt △ABC中,tanA= 。
例11、已知一元二次方程2x2-3x-6=0有两个实数根x1、x2,直线l经过点A(x1+x2,0)、B(0,x1x2),则直线l的解析式为【 度002】
A、y=2x-3 B、y=2x+3 C、y=-2x-3 D、y=-2x+3
【答案】A。
【考点】一元二次方程根与系数的关系,待定系数法求一次函数解析式。
【分析】根据一元二次方程根与系数的关系,求出A,B的坐标,代入直线的解析式,求出k,b的值,从而确定直线的解析式:
由题意知,x1+x2=,x1 x2=-3,∴A(,0),B(0,-3)。
设直线l的解析式为:y=kx+b,把点A,点B的坐标代入,解得,k=2,b=-3,
∴直线l的解析式为:y=2x-3。故选A。
例12、如图,点P(3a,a)是反比例函y=(k>0)与⊙O
的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 度002】
A.y= B.y= C.y= D.y=
【答案】D。
【考点】反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。
【分析】根据反比例函数和圆的中心对称性,图中阴影部分的面积实际上是圆的面积。由勾股定理,可得圆的
半径为。因此,由图中阴影部分的面积为10π可得,解得a=2(因果点P在第一象限,
a>0,负数舍去)。∴点P(6,2)。代入y=,得k=12。则反比例函数的解析式为y=。故选D。
探索发现:同学们,请你体会并总结一下中考的命题方向和趋势:
命题规律三:(点击展开)
涉及到生活中与一次函数数相关的内容,解析式的求法,数学其它知识点与一次函数知识点的综合考查。
第二部分 热点题型精讲
热点题型:
第一类:一次函数概念 第二类:一次函数的图像及性质
第三类:一次函数K值与b的关系 第四类:求解析式及其综合运用
第五类:一次函数与生活知识的应用
第一类:一次函数概念
1、下列函数:①y=x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A、1 B、2 C、3 D、4
考点:一次函数的定义.
分析:根据一次函数的定义条件进行逐一分析即可.
解答:解:①y=x是一次函数;
②y=是一次函数;
③y=自变量次数不为1,故不是一次函数;
④y=2x+1是一次函数.
故选C.
点评:本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
2、在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用关系式y=35x+20表示,这个关系式符合的数学模型是( )
A、正比例函数 B、反比例函数 C、二次函数 D、一次函数
考点:一次函数的定义.
分析:根据一次函数的定义解答即可.
解答:解:∵关系式y=35x+20符合一次函数的形式,
∴这个关系式符合的数学模型是一次函数.
故选D.
点评:本题考查一次函数的定义,即形如y=kx+b,(k≠0,k、b为常数)的函数叫一次函数.
第二类:一次函数的图像及性质
3、函数的图象如图所示,那么函数的图象大致是【 度002】
A B C D
【答案】C。
【考点】一次函数和反比例函数的图象。
【分析】∵反比例函数的图象位于第二、四象限,∴<0。
∵<0,∴函数的图象过二、四象限.
又∵->0,∴函数的图象与y轴相交于正半轴。
第三类:一次函数K值与b的关系
4、一次函数y=(k-2)x+3的图象如图所示,则k的取值范围是( )
A、k>2 B、k<2 C、k>3 D、k<3
考点:一次函数图象与系数的关系.
专题:探究型.
分析:先根据一次函数的图象得到关于k的不等式,求出k的取值范围即可.
解答:解:一次函数的图象过二、四象限可知,k-2<0,
解得k<2.
故选B.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0时,函数的图象过二、四象限.
5、直线y=3x+b 与两坐标轴围成的三角形面积为6,求与y轴的交点坐标( )
A、(0,2) B、(0,-2)(0,2) C、(0,6) D、(0,6)、(0,-6)
考点:一次函数的图象;点的坐标;一次函数图象上点的坐标特征.
专题:探究型.
分析:先令x=0用b表示出y的值,再令y=0得出x的值,根据三角形的面积公式及绝对值的性质求出b的值即可.
解答:解:令x=0,则y=b,令y=0,则x=-6,
∵直线y=3x+b 与两坐标轴围成的三角形面积为6,
∴|b|×|-1|=6,即b=6,
∴b=±6,
∴y轴的交点坐标为(0,6),(0,-6).
故选D.
点评:本题考查的是一次函数的图象及一次函数图象上点的坐标特点、三角形的面积公式,熟知一次函数的图象是直线是解答此题的关键.
第四类:求解析式及其综合运用
6、在平面直角坐标系中,把直线y=x向左平移一个单位长度后,其直线解析式为( )
A、y=x+1 B、y=x-1 C、y=x D、y=x-2
考点:一次函数图象与几何变换.
专题:探究型.
分析:根据“左加右减”的原则进行解答即可.
解答:解:由“左加右减”的原则可知,在平面直角坐标系中,把直线y=x向左平移一个单位长度后,
其直线解析式为y=x+1.
故选A.
点评:本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
7、如图,点P(3a,a)是反比例函y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 度002】
A.y= B.y= C.y= D.y=
考点:反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。
专题:探究型
分析:根据反比例函数和圆的中心对称性,图中阴影部分的面积实际上是圆的面积。
解答:由勾股定理,可得圆的半径为。因此,由图中阴影部分的面积为10π可得,解得a=2(因果点P在第一象限)
故选D.
点评:本题考查反比例函数和圆的中心对称性,勾股定理,曲线上点的坐标与方程的关系。熟练运用勾股定理是解此题的关键。
8、以下是2002年3月12日《南国早报》刊登的南宁市自来水价格调整表:
南宁市自来水价格调整表(部分)单位:元/立方米
用水类别 现行水价 拟调整水价一、居民生活用水 0.72
1、一户一表
第一阶梯:月用水量0~30立方米/户 0.82
第二阶梯:月用水量超过30立方米/户部分 1.23
则调整水价后某户居民月用水量x(立万米)与应交水费y(元)的函数图象是( )
A、 B 、 C、 D、
考点:一次函数的图象;一次函数的应用.
分析:根据题意:函数的图象为分段函数,两段均为一次函数,且当x>50时,收费更高,故直线倾斜程度变大,据此作出选择.
解答:解:根据图中信息,列出函数解析式得:①y=0.82x(0<x<30);②y=1.23x(30<x<50).故选C.
点评:本题要求学生根据题意,结合实际情况,判断函数的图象.
第五类:一次函数与生活知识的应用
9、直线y=-x+m与直线y=x+2相交于y轴上的点C,与x轴分别交于点A、B。
(1)求A、B、C三点的坐标;(3分)
(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(4分)
(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离(可用含θ的三角函数式表示)。(5分)
【答案】解:(1)直线y= x+2中令x=0,得y=2,
∴C点的坐标为(0,2)。
把C(0,2)代入直线y=-x+m,得m=2,
∴直线y=-x+m解析式是y=-x+2。
令y=0,得x=2,则A点的坐标是(2,0),
在y= x+2中令y=0,得x=,则B的坐标是(,0)。
(2)根据A、B、C的坐标得到OC=2,OA=2,OB=,根据锐角三角函数定义,得tan∠ABC=,∴∠ABC=30°。
又AC=。
连接AE,CE,过点E作EF⊥AB于点F,则∠AEC=60°,
∴△ACE是等边三角形,边长是。
又在Rt△EAF中,AE=,AF=AB=,
∴EF=。
又OF=OA+AF=。
∴点E的坐标为(,),半径是。
(3)分两种情况:
(I)当点P在⊙E外时,如图,连接AN,连接ME并延长交⊙E于另一点Q,连接NQ,则△NQM是直角三角形。
∵∠MQN=∠MAN=∠ANC-∠P=∠ABC-∠P=30°-θ,
∴在Rt△NQM中,MN=QMsin∠MQN,
即MN=sin(30°-θ)。
(II)当点P在⊙E内时,如图,连接AN,连接ME并延长交⊙E于另一点Q,连接NQ,则△NQM是直角三角形。
∵∠ACB=∠BCO-∠ACO=60°-45°=15°。
∴∠MQN=∠MAN=∠APB-∠ANB=∠APB-∠ACB =θ-15°。
∴在Rt△NQM中,MN=QMsin∠MQN,
即MN=sin(θ-15°)。
【考点】一次函数综合题,直线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,勾股定理,等边三角形的判定和性质,圆周角定理,弦径定理,三角形外角定理。
【分析】(1)直线y= x+2与y轴的交点可以求出,把这点的坐标就可以求出直线y=-x+m的解析式,两个函数与x轴的交点就可以求出。
(2)根据三角函数可以求出角的度数。由OC、OA、OB的长度,根据勾股定理、等边三角形的判定和性质、弦径定理可求出点E的坐标和⊙E的半径。
(3)分点P在⊙E外和点P在⊙E内两种情况讨论即可。
点评:本题必须熟练运用直线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,勾股定理,等边三角形的判定和性质,圆周角定理,弦径定理,三角形外角定理。
第三部分 名师押题
名师押题
1、下列函数①y=πx,②y=2x-1,③,④y=2-1-3x,⑤y=x2-1中,是一次函数的有( )
A、4个 B、3个 C、2个 D、1个
考点:一次函数的定义.分析:根据一次函数的定义条件进行逐一分析即可.
解答:解:①y=πx是一次函数;
②y=2x-1是一次函数;
③y=πx ,自变量次数不为1,不是一次函数;
④y=2-1-3x是一次函数;
⑤y=x2-1,自变量次数不为1,不是一次函数.
故选B.点评:本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
2.已知正比例函数y=-kx和一次函数y=kx-2(x为自变量),它们在同一坐标系内的图象大致是( )
A、 B、 C、 D、
考点:一次函数的图象;正比例函数的图象.
分析:分k大于0和k小于0两种情况讨论.k>0时,分别画出两函数图象;k<0时分别画出两函数图象;与选项中图象对照.符合题意的即为正确答案.
解答:解:分两种情况:(1)当k>0时,正比例函数y=-kx的图象过原点、第一、三象限,一次函数y=kx-2的图象经过第一、三、四象限,选项A符合;
(2)当k<0时,正比例函数y=-kx的图象过原点、第二、四象限,一次函数y=kx-2的图象经过第二、三、四象限,无选项符合.
故选A.
点评:一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
3.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )
A、x>0 B、x<0 C、x>2 D、x<2
考点:一次函数的图象.
专题:数形结合.
分析:根据函数图象可知,此函数为减函数,图象与x轴的交点坐标为(2,0),由此可得出答案.
解答:解:根据图象和数据可知,当y<0即直线在x轴下方时,x的取值范围是x>2.
故选C.
点评:本题考查一次函数的图象,考查学生的分析能力和读图能力.
4.在地表以下不太深的地方,温度y(℃)与所处的深度x(km)之间的关系可以近似用关系式y=35x+20表示,这个关系式符合的数学模型是( )
A、正比例函数 B、反比例函数 C、二次函数 D、一次函数
考点:一次函数的定义.
分析:根据一次函数的定义解答即可.
解答:解:∵关系式y=35x+20符合一次函数的形式,
∴这个关系式符合的数学模型是一次函数.
故选D.
点评:本题考查一次函数的定义,即形如y=kx+b,(k≠0,k、b为常数)的函数叫一次函数.
5.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是( )
A、m<0 B、m>0 C、m<2 D、m>2
考点:一次函数的性质.
专题:探究型.
分析:根据一次函数的性质列出关于m的不等式,求出m的取值范围即可.
解答:解:∵一次函数y=(2-m)x-2的函数值y随x的增大而减小,
∴2-m<0,
∴m>2.
故选D.
点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0时,y随x的增大而减小.
6. P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,则下列判断正确的是( )
A、y1>y2 B、y1<y2 C、当x1<x2时,y1>y2 D、当x1<x2时,y1<y2
考点:正比例函数的性质.
分析:根据正比例函数图象的性质可知.
解答:解:根据k<0,得y随x的增大而减小.
故选C.
点评:了解正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.
7.已知一次函数y=kx+b的图象经过第一、二、三象限,则b的值可以是( )
A、-2 B、-1 C、0 D、2
考点:一次函数图象与系数的关系.
专题:探究型.
分析:根据一次函数的图象经过第一、二、三象限判断出b的符号,再找出符合条件的b的可能值即可.解答:解:∵一次函数的图象经过第一、二、三象限,
∴b>0,
∴四个选项中只有2符合条件.
故选D.
点评:本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当b<0时,函数图象与y轴相交于负半轴.
8.如图的坐标平面上,有一条通过点(-3,-2)的直线L.若四点(-2,a)、(0,b)、(c,0)、(d,-1)在L上,则下列数值的判断,何者正确( )
A、a=3 B、b>-2 C、c<-3 D、d=2
考点:一次函数图象上点的坐标特征.
专题:数形结合.
分析:根据函数的图象可判断出函数的增减性,从而结合选项即可判断各选项正确与否.
解答:解:由题意得:此函数为减函数,
A、-2>-3,故a<-2,故本选项错误;
B、-3<0,故-2>b,故本选项错误;
C、0>-2,故c<-3,故本选项正确;
D、-1>-2,故b<-3,故本选项错误.
故选C.
点评:本题考查一次函数图象上点的坐标特征,解答本题的关键是掌握函数的增减性,另外本题还可以利用特殊值设出符合题意的函数解析式,然后代入判断.
9.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(a,b),且2a+b=6,则直线AB的解析式是( )
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+6
考点:一次函数图象与几何变换.
专题:数形结合.
分析:平移时k的值不变,只有b发生变化.再把相应的点代入即可.
解答:解:原直线的k=-2,向上平移后得到了新直线,那么新直线的k=-2.
∵直线AB经过点(a,b),且2a+b=6.
∴直线AB经过点(a,6-2a).
可设新直线的解析式为y=-2x+b1,
∴6-2a=-2a+b1,
则b1=6,
∴直线AB的解析式是y=-2x+6.
故选D.
点评:求直线平移后的解析式时要注意平移k值不变.
10.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程是2x+b=0的解是x=2。
考点:一次函数与一元一次方程.
专题:计算题.
分析:根据直线y=2x+b与x轴的交点坐标是(2,0),求得b,再把b代入方程2x+b=0,求解即可.
解答:解:把(2,0)代入y=2x+b,
得:b=-4,把b=-4代入方程2x+b=0,
得:x=2.
故填2.
点评:考查了一次函数与坐标轴的交点坐标问题,还考查了方程解的定义.
11、目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
A、y=0.05x B、y=5xC、y=100x D、y=0.05x+100
考点:根据实际问题列一次函数关系式.
分析:每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
解答:解:y=100×0.05x,
即y=5x.
故选B.
点评:本题主要考查了根据实际问题列一次函数解析式,正确表示出一分钟滴的水的体积是解题的关键.
12.如图,函数y=mx-4m的图象分别交x轴、y轴于点N、M,线段MN上两点A、B在x轴上的垂足分别为A1、B1,若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( )
A、S1>S2 B、S1=S2 C、S1<S2 D、不确定的
考点:一次函数综合题.
分析:设A(a,ma-4m),B(b,mb-4m)表示出S1和S2,然后让两式相减即可比较出大小.
解答:解:设A(a,ma-4m),B(b,mb-4m),则:
S1=1 2a×(ma-4m),S2=1/2b(mb-4m)
S1-S2=1 2(ma2-mb2)-1 24m(a-b)=(a-b){1 2m(a+b)-1 2.4m}
又∵OA1+OB1>4
∴1 2m(a+b)-1 24m=1/2m(a+b-4)<0
∴S1-S2>0
故选A.
点评:本题考查三角形和坐标系的结合,属于比较好的题.同学们要注意掌握这类数形结合题目的解答.
A.
B.
C.
D.
A.
B.
C.
D.
A
O
B
C
同课章节目录
