沪科版数学八年级下册 18.2 勾股定理的逆定理课件(共14张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.2 勾股定理的逆定理课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
18.2 勾股定理的逆定理
复习
勾股定理:
如果一个三角形是直角三角形,那么它的两条直角边的平方和,等于斜边的平方。
按照这种做法真能得到一个直角三角形吗?
课本58页思考1.
据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图,这样围成的三角形中,最长边所对的角就是直角。
古埃及人曾用下面的方法得到直角:
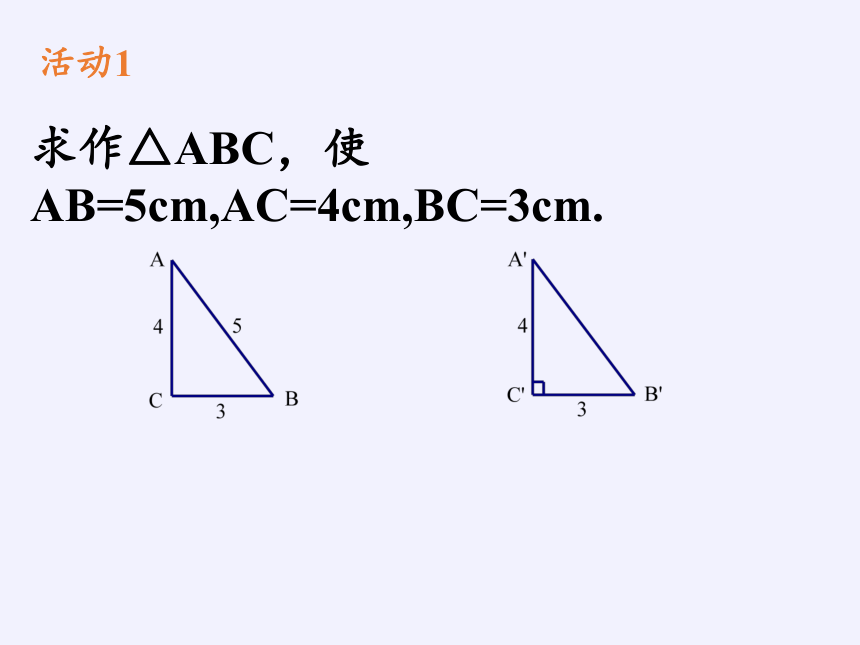
活动1
求作△ABC,使AB=5cm,AC=4cm,BC=3cm.
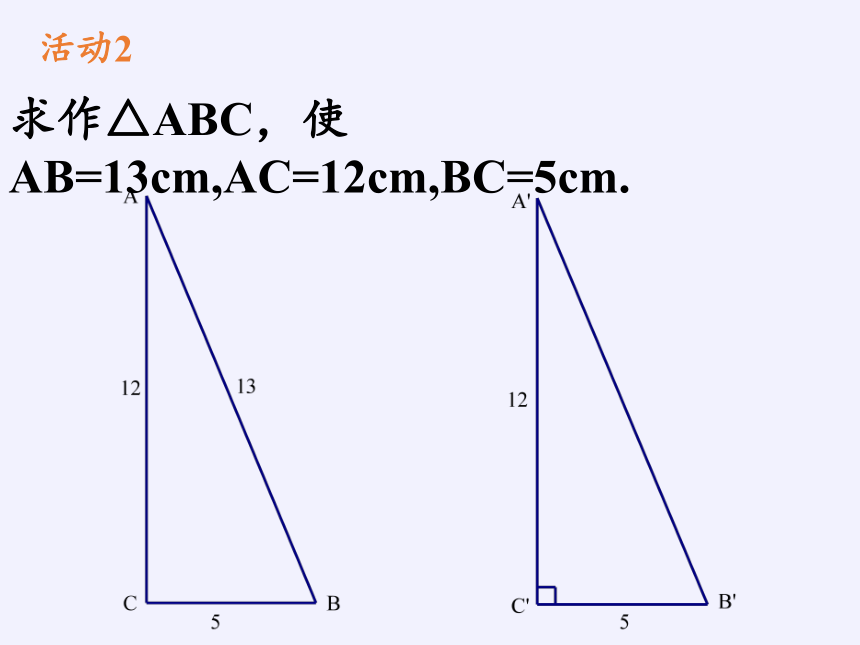
活动2
求作△ABC,使AB=13cm,AC=12cm,BC=5cm.
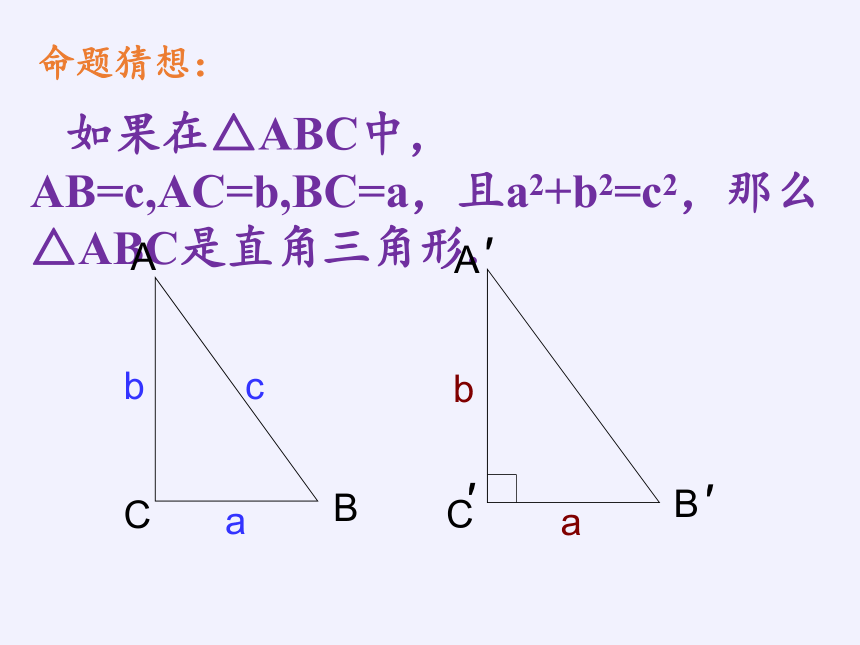
命题猜想:
如果在△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,那么△ABC是直角三角形.
a
b
c
A
C
B
A
′
B
′
C
′
a
b
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理的逆定理
a
b
c
A
C
B
几何语言表述:
在△ABC中,
如果BC2+AC2=AB2,
那么△ABC是直角三角形.
例1
判断下面以a、b、c为边长的△ABC是不是直角三角形?如果是,指出哪条边所对的角是直角.
② a=0.5,b=1.2,c=1.3;
(1)a=7,b=24,c=25;
(3)a=7,b=8,c=11
(2) ① a=30,b=50,c=40;
例2
A
B
C
D
4cm
5cm
1cm
如图:在四边形ABCD中,AB=4cm,BC=5cm,CD= AD=1cm,AD⊥CD,求四边形ABCD的面积.
变一变
A
B
C
D
2.4cm
1.8cm
1cm
如图:在四边形ABCD中,AB=2.4cm,BC=1.8cm,CD= AD=1cm,AD⊥CD,求四边形ABCD的面积.
3cm
课堂小结
经过这节课的学习,大家总共学
习了哪些内容?有什么感悟?
通过一节课的学习,相信大家也都累了,最后我们来做一个游戏好吗?
先请同学们任意说一个正整数,老师会接着立即再说出两个正整数,能够使这三个正整数成为一组勾股数。
有谁知道这其中的规律呢?请有兴趣的同学课下自己先讨论!
必做题:教材59页练习1、3、4
选做题
1.如图:在正方形ABCD中,
F为AD的中点,
求证:BF⊥FE .
2.如图:在四边形ABCD
中,AB=BC=2cm,CD=
AD=1cm,∠B=60 °,
求四边形ABCD的面积.
B
A
F
E
D
C
A
D
1cm
2cm
2cm
B
C
60°
谢 谢
18.2 勾股定理的逆定理
复习
勾股定理:
如果一个三角形是直角三角形,那么它的两条直角边的平方和,等于斜边的平方。
按照这种做法真能得到一个直角三角形吗?
课本58页思考1.
据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后,用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图,这样围成的三角形中,最长边所对的角就是直角。
古埃及人曾用下面的方法得到直角:
活动1
求作△ABC,使AB=5cm,AC=4cm,BC=3cm.
活动2
求作△ABC,使AB=13cm,AC=12cm,BC=5cm.
命题猜想:
如果在△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,那么△ABC是直角三角形.
a
b
c
A
C
B
A
′
B
′
C
′
a
b
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理的逆定理
a
b
c
A
C
B
几何语言表述:
在△ABC中,
如果BC2+AC2=AB2,
那么△ABC是直角三角形.
例1
判断下面以a、b、c为边长的△ABC是不是直角三角形?如果是,指出哪条边所对的角是直角.
② a=0.5,b=1.2,c=1.3;
(1)a=7,b=24,c=25;
(3)a=7,b=8,c=11
(2) ① a=30,b=50,c=40;
例2
A
B
C
D
4cm
5cm
1cm
如图:在四边形ABCD中,AB=4cm,BC=5cm,CD= AD=1cm,AD⊥CD,求四边形ABCD的面积.
变一变
A
B
C
D
2.4cm
1.8cm
1cm
如图:在四边形ABCD中,AB=2.4cm,BC=1.8cm,CD= AD=1cm,AD⊥CD,求四边形ABCD的面积.
3cm
课堂小结
经过这节课的学习,大家总共学
习了哪些内容?有什么感悟?
通过一节课的学习,相信大家也都累了,最后我们来做一个游戏好吗?
先请同学们任意说一个正整数,老师会接着立即再说出两个正整数,能够使这三个正整数成为一组勾股数。
有谁知道这其中的规律呢?请有兴趣的同学课下自己先讨论!
必做题:教材59页练习1、3、4
选做题
1.如图:在正方形ABCD中,
F为AD的中点,
求证:BF⊥FE .
2.如图:在四边形ABCD
中,AB=BC=2cm,CD=
AD=1cm,∠B=60 °,
求四边形ABCD的面积.
B
A
F
E
D
C
A
D
1cm
2cm
2cm
B
C
60°
谢 谢
