2021-2022学年人教版八年级下册数学第18章《平行四边形》(3)(含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学第18章《平行四边形》(3)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 671.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
2.菱形的对角线,相交于点,且,,则四边形是( )
A.梯形 B.矩形 C.菱形 D.正方形
3.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为( )
A.36° B.54° C.64° D.72°
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
5.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7 B.8 C.9 D.10
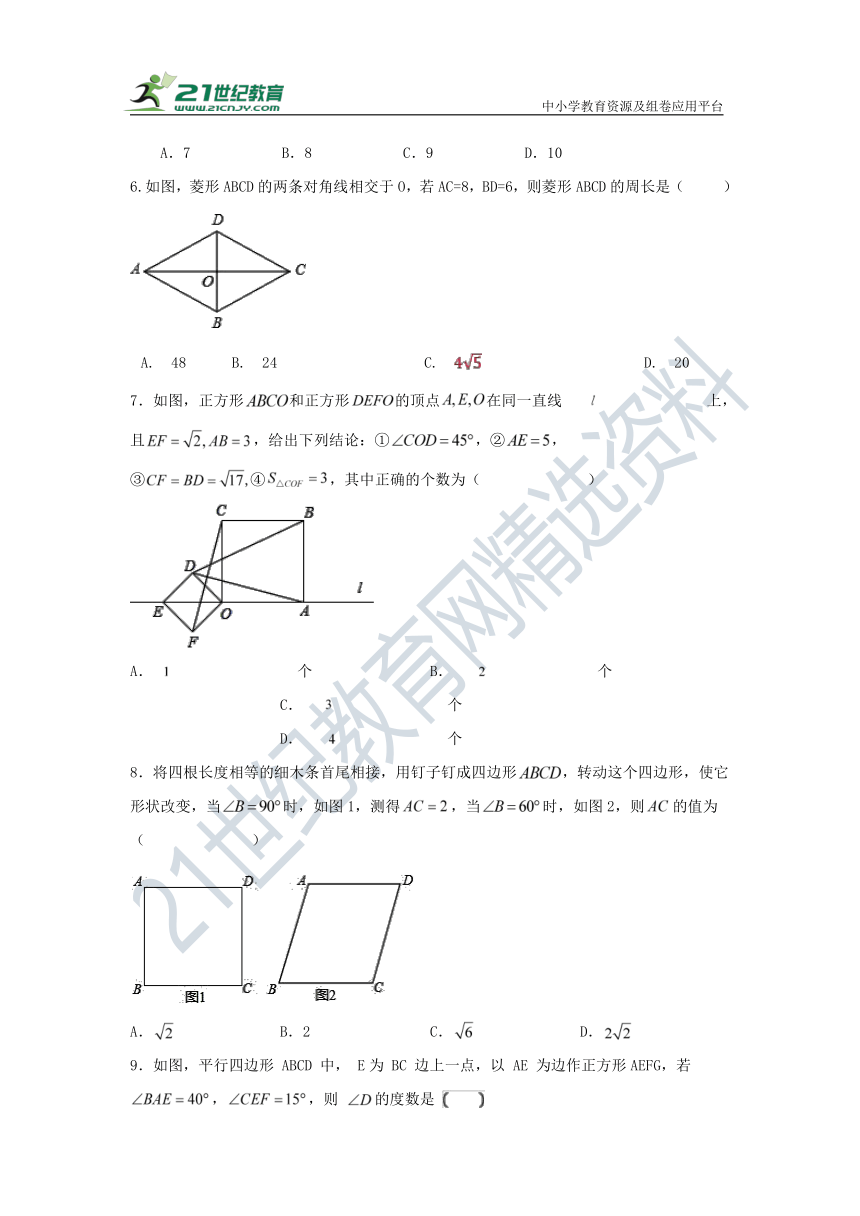
6.如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
A. 48 B. 24 C. D. 20
7.如图,正方形和正方形的顶点在同一直线上,且,给出下列结论:①,②,③④,其中正确的个数为( )
A.个 B.个 C.个 D.个
8.将四根长度相等的细木条首尾相接,用钉子钉成四边形,转动这个四边形,使它形状改变,当时,如图1,测得,当时,如图2,则的值为( )
A. B.2 C. D.
9.如图,平行四边形 ABCD 中, E为 BC 边上一点,以 AE 为边作正方形AEFG,若 ,,则 的度数是
A. B. C. D.
10.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
二、填空题(每题3分,共24分)
11.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为,则点E的坐标为______________.
12.如图,矩形中,,,点是边上动点,则的最小值为______.
13.将矩形ABCD按如图所示的方式折叠得到菱形AECF若BC=,则BE的长是_____.
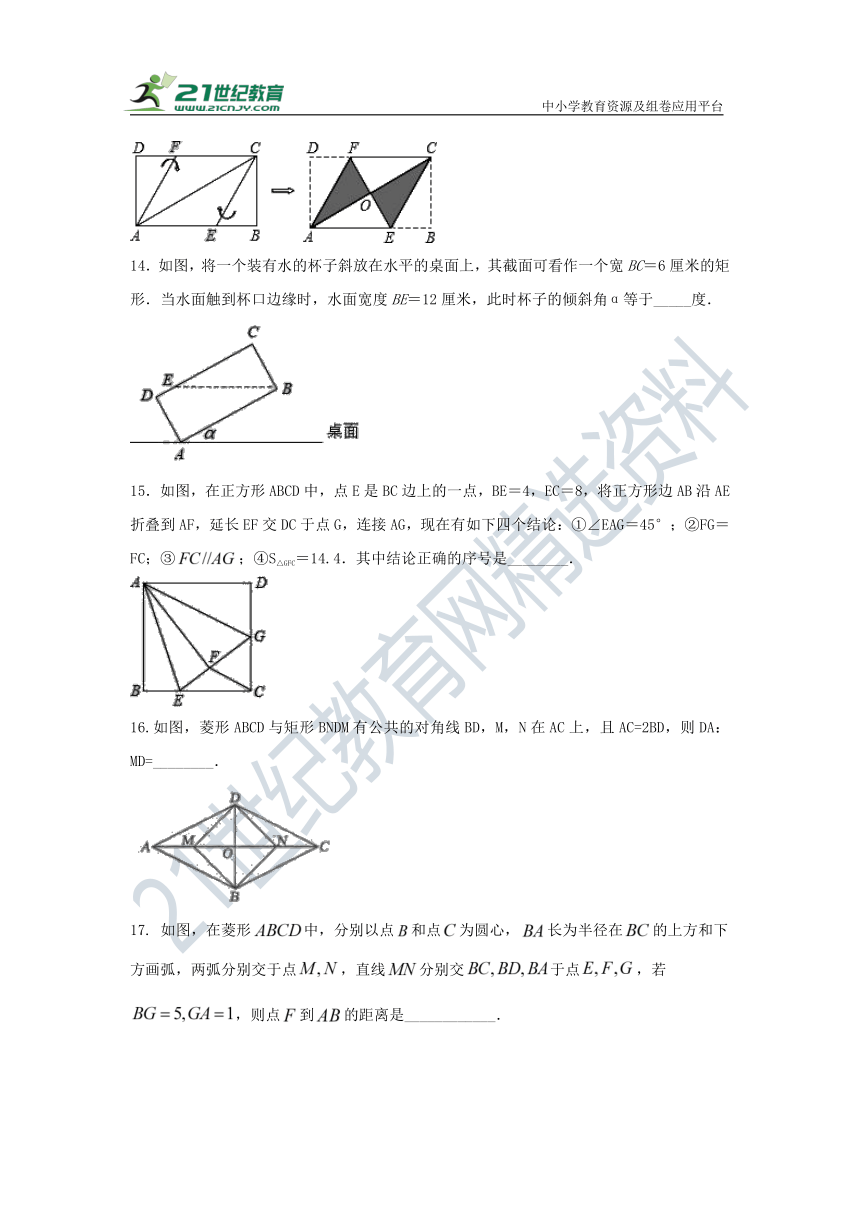
14.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于_____度.
15.如图,在正方形ABCD中,点E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于点G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③;④S△GFC=14.4.其中结论正确的序号是________.
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17. 如图,在菱形中,分别以点和点为圆心,长为半径在的上方和下方画弧,两弧分别交于点,直线分别交于点,若,则点到的距离是____________.
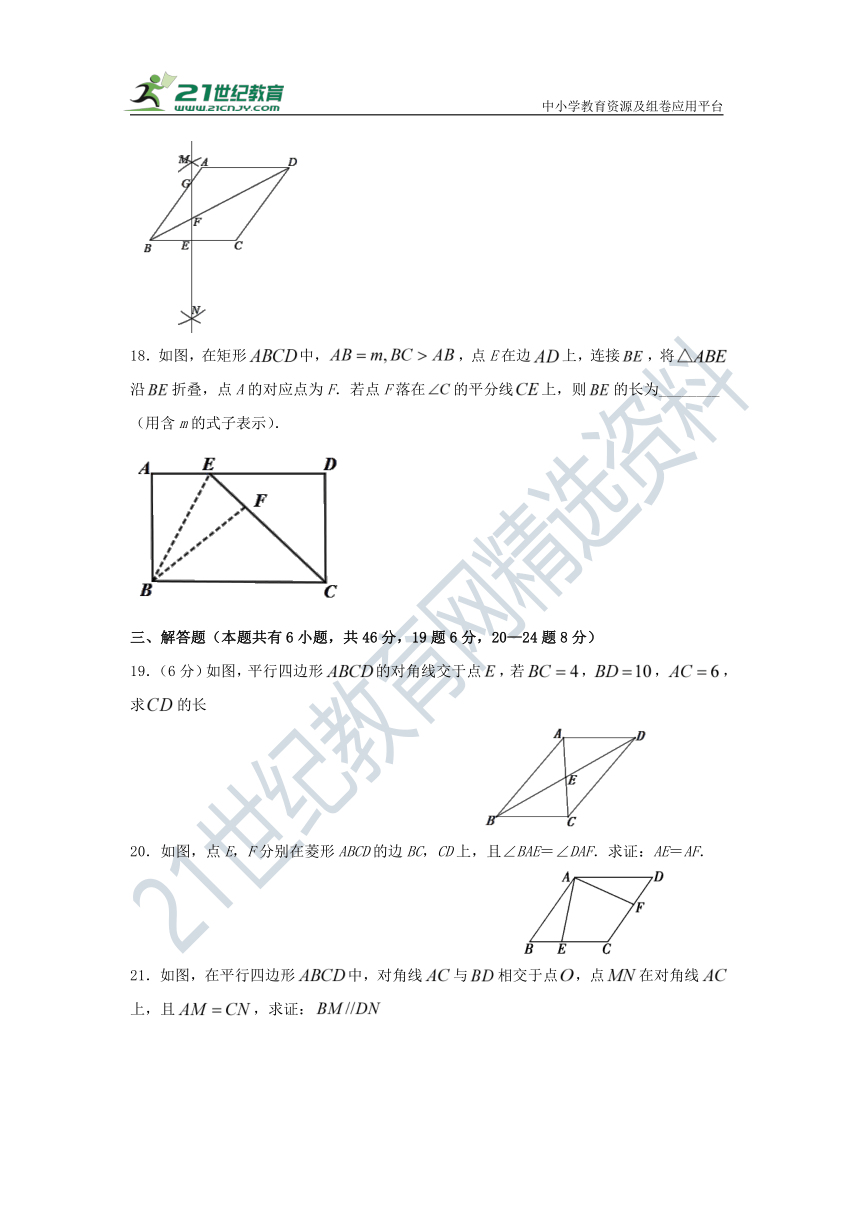
18.如图,在矩形中,,点E在边上,连接,将沿折叠,点A的对应点为F.若点F落在的平分线上,则的长为________(用含m的式子表示).
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
22、(8分)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)试说明△BDE≌△CDF;
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
23.如图,DB∥AC,且DB=AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?
24.(8分)如图,为平行四边形,,,交的延长线于点,交于点.
⑴ 求证:;
⑵ 若,,,求的长;
⑶ 在⑵的条件下,求四边形的面积.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D A D D B B B
二.填空题
11.
12.3
13.1
14.30.
15.①③④
16.
17..
18.
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、解:(1)∵CF∥BE,
∴∠FCD=∠EBD.
∵D是BC的中点,
∴CD=BD.
∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
(2)四边形BECF是平行四边形.
理由:∵△CDF≌△BDE,
∴DF=DE,DC=DB.
∴四边形BECF是平行四边形.
23.(1)证明:∵E是AC中点,
∴EC=AC.
∵DB=AC,
∴DB∥EC.
又∵DB∥EC,
∴四边形DBCE是平行四边形.
∴BC=DE.
(2)添加AB=BC.
理由:∵DB∥AE,DB=AE
∴四边形DBEA是平行四边形.
∵BC=DE,AB=BC,
∴AB=DE.
∴ ADBE是矩形.
24. 【答案】
⑴ 证明:延长交于点
∵,
∴四边形是平行四边形
∴,为的中点,,∴.
⑵ 由⑴得是的中位线
故
又∵,四边形是平行四边形
∴
又∵
∴在中利用勾股定理得
∴.
⑶ 可将四边形的面积分为两部分,梯形和三角形,在中利用勾股定理得,由是的中位线得,四边形是平行四边形得,,
∴梯形面积为:;
由和可证得三角形是直角三角形,
其面积为:,
∴四边形的面积为.
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法正确的是( )
A.有一组对角是直角的四边形一定是矩形
B.一条对角线被另一条对角线垂直平分的四边形是菱形
C.对角互补的平行四边形是矩形
D.对角线相等的四边形是矩形
2.菱形的对角线,相交于点,且,,则四边形是( )
A.梯形 B.矩形 C.菱形 D.正方形
3.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为( )
A.36° B.54° C.64° D.72°
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是( )
A.2.2cm B.2.3cm C.2.4cm D.2.5cm
5.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7 B.8 C.9 D.10
6.如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
A. 48 B. 24 C. D. 20
7.如图,正方形和正方形的顶点在同一直线上,且,给出下列结论:①,②,③④,其中正确的个数为( )
A.个 B.个 C.个 D.个
8.将四根长度相等的细木条首尾相接,用钉子钉成四边形,转动这个四边形,使它形状改变,当时,如图1,测得,当时,如图2,则的值为( )
A. B.2 C. D.
9.如图,平行四边形 ABCD 中, E为 BC 边上一点,以 AE 为边作正方形AEFG,若 ,,则 的度数是
A. B. C. D.
10.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
二、填空题(每题3分,共24分)
11.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为,则点E的坐标为______________.
12.如图,矩形中,,,点是边上动点,则的最小值为______.
13.将矩形ABCD按如图所示的方式折叠得到菱形AECF若BC=,则BE的长是_____.
14.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于_____度.
15.如图,在正方形ABCD中,点E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于点G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③;④S△GFC=14.4.其中结论正确的序号是________.
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17. 如图,在菱形中,分别以点和点为圆心,长为半径在的上方和下方画弧,两弧分别交于点,直线分别交于点,若,则点到的距离是____________.
18.如图,在矩形中,,点E在边上,连接,将沿折叠,点A的对应点为F.若点F落在的平分线上,则的长为________(用含m的式子表示).
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
22、(8分)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)试说明△BDE≌△CDF;
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
23.如图,DB∥AC,且DB=AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?
24.(8分)如图,为平行四边形,,,交的延长线于点,交于点.
⑴ 求证:;
⑵ 若,,,求的长;
⑶ 在⑵的条件下,求四边形的面积.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D A D D B B B
二.填空题
11.
12.3
13.1
14.30.
15.①③④
16.
17..
18.
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、解:(1)∵CF∥BE,
∴∠FCD=∠EBD.
∵D是BC的中点,
∴CD=BD.
∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
(2)四边形BECF是平行四边形.
理由:∵△CDF≌△BDE,
∴DF=DE,DC=DB.
∴四边形BECF是平行四边形.
23.(1)证明:∵E是AC中点,
∴EC=AC.
∵DB=AC,
∴DB∥EC.
又∵DB∥EC,
∴四边形DBCE是平行四边形.
∴BC=DE.
(2)添加AB=BC.
理由:∵DB∥AE,DB=AE
∴四边形DBEA是平行四边形.
∵BC=DE,AB=BC,
∴AB=DE.
∴ ADBE是矩形.
24. 【答案】
⑴ 证明:延长交于点
∵,
∴四边形是平行四边形
∴,为的中点,,∴.
⑵ 由⑴得是的中位线
故
又∵,四边形是平行四边形
∴
又∵
∴在中利用勾股定理得
∴.
⑶ 可将四边形的面积分为两部分,梯形和三角形,在中利用勾股定理得,由是的中位线得,四边形是平行四边形得,,
∴梯形面积为:;
由和可证得三角形是直角三角形,
其面积为:,
∴四边形的面积为.
