沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌课件(共25张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.4 综合与实践 多边形的镶嵌课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 08:31:05 | ||
图片预览







文档简介
(共25张PPT)
19.4 综合与实践 多边形的镶嵌
共同特征
无缝隙,不重叠
好漂亮的地板!这是怎么铺设的
平面图形的镶嵌
平面镶嵌:用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里叫做平面镶嵌.
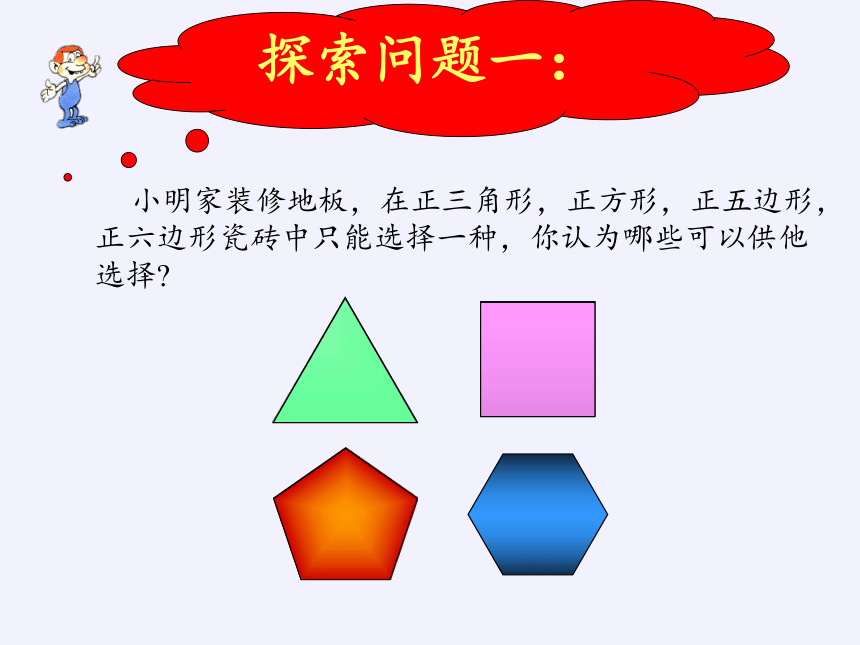
小明家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种,你认为哪些可以供他选择
探索问题一:
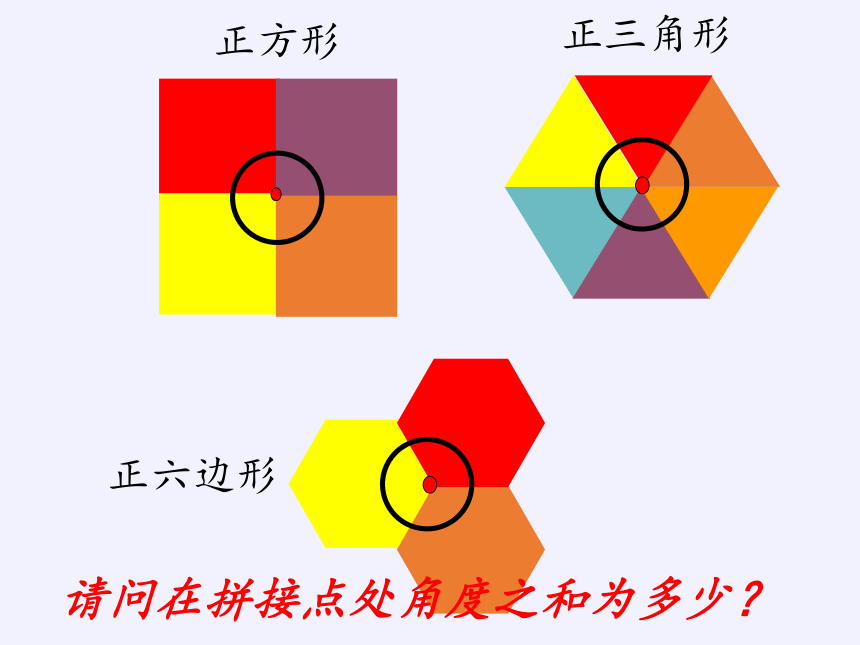
正方形
正三角形
正六边形
请问在拼接点处角度之和为多少?
1
2
3
∠1+∠2+∠3=
请问在拼接点处角度之和为多少?
我的发现:
拼接点处的各个角度数之和必须等于360°。
正多边形可以镶嵌的条件:
360o能被正多边形的内角度数整除。
几何画板镶嵌.gsp
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?
四边形呢?
探索问题二:
几何画板镶嵌.gsp
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
∴任意三角形能镶嵌成平面图案。
几何画板镶嵌.gsp
∵∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
∴任意四边形能镶嵌成平面图案。
几何画板镶嵌.gsp
用全等的三角形(或四边形)密铺的方法
取几个三角形(或四边形)的不同顶点处的内角围绕一点拼成360度,并使等边重合。
1
2
3
4
5
6
1
2
3
4
问题情景:
小新搬新家了,他想用两种正多边形来镶嵌房间的地板,请你帮忙设计一个方案吧?
探索问题三:
活动一:
用边长相等的正三角形和正方形,能否镶嵌成平面图案?请你试一试!
用边长相等的正三角形和正六边形进行平面镶嵌,你能拼出几种不同的图案?
活动二:
你能找到它们的拼接点吗?
2m+3n=12
m=3
n=2
m·60° +n·90° =360°
解:设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,则有
∵ m,n 为正整数
∴解为
m+2n=6
解:设在一个拼接点周围有 m 个正三角形的角,n 个正六边形的角,
∵ m,n 为正整数
你知道正三角形及正六边形各需要多少吗?
需要两个正三角形及两个正六边形镶嵌。
m·60 +n·120 =360
。
。
。
m=2
n=2
∴解为
m=4
n=1
或需要四个正三角形及一个正六边形镶嵌。
课外思考:还有没有其他的两种多边形组合镶嵌的形式呢?
+
+
几何画板镶嵌.gsp
例如正五边形和正八边形它们单独用同一种不能镶嵌,但与三角形、四边形就能镶嵌成平面图案.
正三角形
正六边形
正方形
三种正多边形的平面镶嵌
欣赏
不一样的镶嵌
1.多边形能进行平面镶嵌的特征:
无缝隙,不重叠
2.多边形能进行平面镶嵌的条件:
拼接在同一点的各个角的度数和360°.
谈一谈:
本节课你的收获……
3. 用一种多边形平面镶嵌时,三角形,四边形,正六边形都能平面镶嵌.其他正多边形不能平面镶嵌.(360o能被正多边形的内角度数整除)
请你用课上所学知识,自己独立设计一个可以平面镶嵌的“基本单元”构成一幅镶嵌艺术画. ,
作业:
几何画板镶嵌.gsp
谢 谢
19.4 综合与实践 多边形的镶嵌
共同特征
无缝隙,不重叠
好漂亮的地板!这是怎么铺设的
平面图形的镶嵌
平面镶嵌:用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里叫做平面镶嵌.
小明家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种,你认为哪些可以供他选择
探索问题一:
正方形
正三角形
正六边形
请问在拼接点处角度之和为多少?
1
2
3
∠1+∠2+∠3=
请问在拼接点处角度之和为多少?
我的发现:
拼接点处的各个角度数之和必须等于360°。
正多边形可以镶嵌的条件:
360o能被正多边形的内角度数整除。
几何画板镶嵌.gsp
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?
四边形呢?
探索问题二:
几何画板镶嵌.gsp
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
∴任意三角形能镶嵌成平面图案。
几何画板镶嵌.gsp
∵∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
∴任意四边形能镶嵌成平面图案。
几何画板镶嵌.gsp
用全等的三角形(或四边形)密铺的方法
取几个三角形(或四边形)的不同顶点处的内角围绕一点拼成360度,并使等边重合。
1
2
3
4
5
6
1
2
3
4
问题情景:
小新搬新家了,他想用两种正多边形来镶嵌房间的地板,请你帮忙设计一个方案吧?
探索问题三:
活动一:
用边长相等的正三角形和正方形,能否镶嵌成平面图案?请你试一试!
用边长相等的正三角形和正六边形进行平面镶嵌,你能拼出几种不同的图案?
活动二:
你能找到它们的拼接点吗?
2m+3n=12
m=3
n=2
m·60° +n·90° =360°
解:设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,则有
∵ m,n 为正整数
∴解为
m+2n=6
解:设在一个拼接点周围有 m 个正三角形的角,n 个正六边形的角,
∵ m,n 为正整数
你知道正三角形及正六边形各需要多少吗?
需要两个正三角形及两个正六边形镶嵌。
m·60 +n·120 =360
。
。
。
m=2
n=2
∴解为
m=4
n=1
或需要四个正三角形及一个正六边形镶嵌。
课外思考:还有没有其他的两种多边形组合镶嵌的形式呢?
+
+
几何画板镶嵌.gsp
例如正五边形和正八边形它们单独用同一种不能镶嵌,但与三角形、四边形就能镶嵌成平面图案.
正三角形
正六边形
正方形
三种正多边形的平面镶嵌
欣赏
不一样的镶嵌
1.多边形能进行平面镶嵌的特征:
无缝隙,不重叠
2.多边形能进行平面镶嵌的条件:
拼接在同一点的各个角的度数和360°.
谈一谈:
本节课你的收获……
3. 用一种多边形平面镶嵌时,三角形,四边形,正六边形都能平面镶嵌.其他正多边形不能平面镶嵌.(360o能被正多边形的内角度数整除)
请你用课上所学知识,自己独立设计一个可以平面镶嵌的“基本单元”构成一幅镶嵌艺术画. ,
作业:
几何画板镶嵌.gsp
谢 谢
