湘教版七年级下册 3.3 公式法(第1课时)课件(共13张PPT)
文档属性
| 名称 | 湘教版七年级下册 3.3 公式法(第1课时)课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
3.3公式法(一)
第三章
复习:运用平方差公式计算:
.(2+a)(a-2);
2). (-4s+t)(t+4s)
. (m +2n )(2n - m )
4). (x+2y) (x-2y)
看谁做得最快最正确!
知识回顾
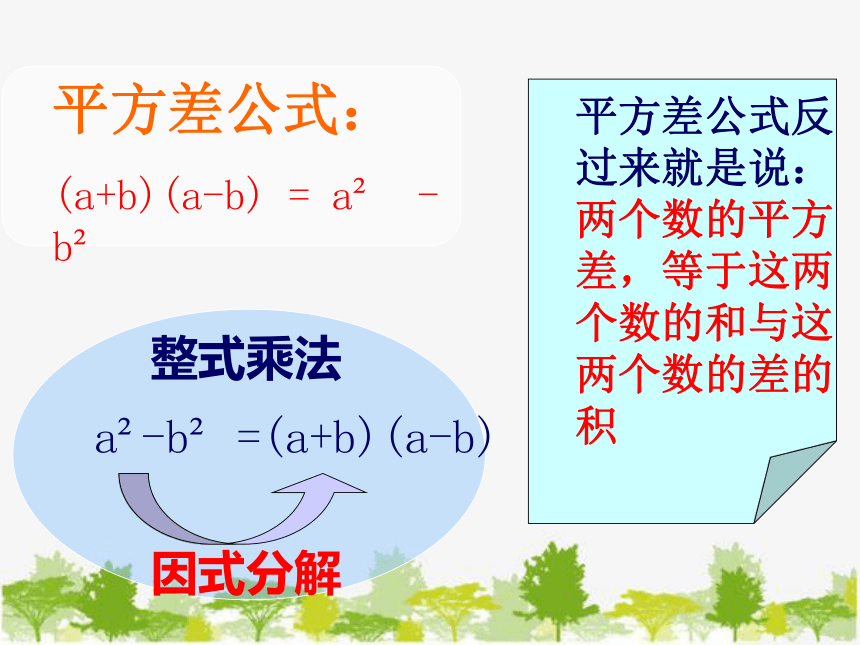
平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积
a -b =(a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a - b
整式乘法
引例:
对照平方差公式怎样将下面的多项式分解因式
1) x - 25 2) 4x - 9y
x - 25= x - 5 =( x + 5)( x-5 )
a - b = ( a + b)( a - b )
4x - 9y =(2x) -(3y) =(2x+3y)(2x-3y)
把 因式分解。
分析 : 可以用平方差公式进行因式分解吗?
解:
例1
因为25x2可以写成(5x)2,所以
能用平方差公式因式分解.
自主预习
像上述例子那样,把乘法公式从右到左地使用,可以把某些类型的多项式因式分解,这种方法叫作公式法.
小 结
解
例2
把 因式分解.
自主探究
=2x·2y
=4xy
把 因式分解.
分析: 可以用平方差公式进行因式分解吗?
可以!因为
解
注意:在例3中,在第一次用平方差公式因式分解后,得到的一个因式 还可以再用平方差公式因式分解,在因式分解中,必须进行到每一个因式都不能再分解为止.
例3
分析 第一步作什么?
先提出公因式x3
把 因式分解.
解:
例4
2、分解因式的步骤:
(1)、优先考虑提公因式法
(2)、其次看是否能用公式
(3)、两者都不行,综合运用两种方法
(4)、务必检查是否分解到底了
1、分解因式的方法
(1)提公因式法
(2)公式法:平方差公式
知识梳理
1.选择题:
1)下列各式能用平方差公式分解因式的是( )
4X +y B. 4 x- (-y) C. -4 X -y D. - X + y
-4a +1分解因式的结果应是 ( )
-(4a+1)(4a-1) B. -( 2a –1)(2a –1)
-(2a +1)(2a+1) D. -(2a+1) (2a-1)
2. 把下列各式分解因式:
1)18-2b 2) x4 –1
D
D
随堂练习
2.把下列多项式因式分解:
3.3公式法(一)
第三章
复习:运用平方差公式计算:
.(2+a)(a-2);
2). (-4s+t)(t+4s)
. (m +2n )(2n - m )
4). (x+2y) (x-2y)
看谁做得最快最正确!
知识回顾
平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积
a -b =(a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a - b
整式乘法
引例:
对照平方差公式怎样将下面的多项式分解因式
1) x - 25 2) 4x - 9y
x - 25= x - 5 =( x + 5)( x-5 )
a - b = ( a + b)( a - b )
4x - 9y =(2x) -(3y) =(2x+3y)(2x-3y)
把 因式分解。
分析 : 可以用平方差公式进行因式分解吗?
解:
例1
因为25x2可以写成(5x)2,所以
能用平方差公式因式分解.
自主预习
像上述例子那样,把乘法公式从右到左地使用,可以把某些类型的多项式因式分解,这种方法叫作公式法.
小 结
解
例2
把 因式分解.
自主探究
=2x·2y
=4xy
把 因式分解.
分析: 可以用平方差公式进行因式分解吗?
可以!因为
解
注意:在例3中,在第一次用平方差公式因式分解后,得到的一个因式 还可以再用平方差公式因式分解,在因式分解中,必须进行到每一个因式都不能再分解为止.
例3
分析 第一步作什么?
先提出公因式x3
把 因式分解.
解:
例4
2、分解因式的步骤:
(1)、优先考虑提公因式法
(2)、其次看是否能用公式
(3)、两者都不行,综合运用两种方法
(4)、务必检查是否分解到底了
1、分解因式的方法
(1)提公因式法
(2)公式法:平方差公式
知识梳理
1.选择题:
1)下列各式能用平方差公式分解因式的是( )
4X +y B. 4 x- (-y) C. -4 X -y D. - X + y
-4a +1分解因式的结果应是 ( )
-(4a+1)(4a-1) B. -( 2a –1)(2a –1)
-(2a +1)(2a+1) D. -(2a+1) (2a-1)
2. 把下列各式分解因式:
1)18-2b 2) x4 –1
D
D
随堂练习
2.把下列多项式因式分解:
