第四章《几何图形初步》复习指导 学案(含答案)
文档属性
| 名称 | 第四章《几何图形初步》复习指导 学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 688.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 09:25:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
《几何图形初步》复习指导
一、课标要求
1.经历观察、测量、折纸、剪切、模型制作,拼摆与简单图案设计等活动过程.发展空间观念.
2.在现实情境中认识线段、射线、直线、角等简单平面图形,了解平面上两条直线的平行和垂直关系.
3.能用字母表示角、线段、互相平行或垂直的直线.
4.会进行线段或角的比较,能估计一个角的大小,会进行有关角度的换算.活动中探索图形性质的过程,了解线段、平行、垂直的有关性质,丰富数学学习的体验,积累操作活动经验,发展有条理地思考与表达.
5.掌握借助三角尺、量角器、方格纸画角、线段、平行线、垂线的简便方法,能进行简单的图案设计,并能表达和交流自己的设计方案.
二、知识结构
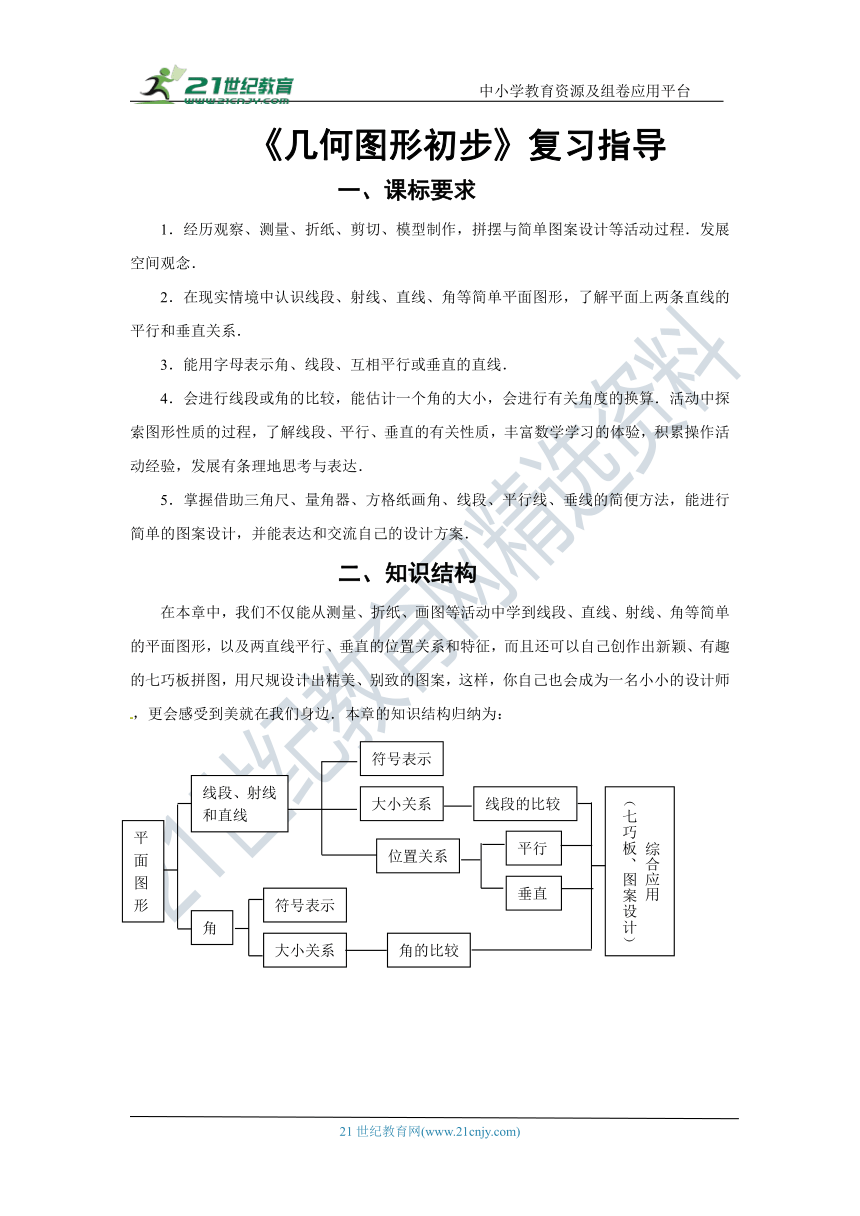
在本章中,我们不仅能从测量、折纸、画图等活动中学到线段、直线、射线、角等简单的平面图形,以及两直线平行、垂直的位置关系和特征,而且还可以自己创作出新颖、有趣的七巧板拼图,用尺规设计出精美、别致的图案,这样,你自己也会成为一名小小的设计师,更会感受到美就在我们身边.本章的知识结构归纳为:
三、要点扫描
本章的要点内容共分“三大板块”
第一板块:线、角的特性
1.线段、射线、直线三者之间的联系与区别,共性与特性
线段 射线 直线
图形
表示方法 线段AB、线段a 射线OM 直线AB、直线l
端点 2个 1个 无
共性 线段、射线、直线都是笔直的.
特性 线段有两个端点,不向任何一旁延伸,可以度量;射线有一个端点,向一旁无限延伸,不能度量;直线没有端点,向两旁无限延伸,不能度量.
联系 射线和线段都是直线的一部分.
2.线段、角的有关知识对比
线段 角
定义 直线上两点之间的部分 1)有公共端点的两条射线组成的图形叫角。这个公共端点叫做角的顶点,两条射线叫做角的边.2)角也可以看成是一条射线绕着端点从起始位置旋转到终止位置所组成的图形.
表示 两种:两个大写英文字母、一个小写英文字母 四种:三个大写英文字母;一个大写英文字母;一个阿拉伯数字;一个小写希腊字母
比较 (1)叠合法(2)度量法 (1)叠合法(2)度量法
度量 (1)测量工具:刻度尺(2)换算:1km=1000m,1m=10dm,1dm=10cm,1cm=10mm (1)测量工具:量角器(2)换算:1周角=2平角=4直角,1平角=2直角,1 =60',1'=60"
和差的表示 (1)和:AC+BC=AB(2)差:AB-AC=BCAB-BC=AC (1)和:∠AOC+∠BOC=∠AOB(2)差:∠AOB-∠AOC=∠BOC
等分点(线) 线段的中点、三等分点等 角的平分线、三等分线等
其他 1.直线的基本性质:两点确定一条直线2.线段的基本性质:两点之间,线段最短3.两点之间的距离:两点之间的线段的长度 角的分类:周角、平角、钝角、直角、锐角
第二板块:平行与垂直
在同一平面,两条直线的位置关系只有两种:①相交 ②平行.
平行 垂直
定义 在同一平面内,不相交的两条直线叫做平行线 当两条直线相交成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫垂足
表示 用符号“∥”表示 用符号“⊥”表示
性质 性质1:经过直线外一点,有且只有一条直线与已知直线平行.性质2(传递性):如果两条直线都和第三条直线平行,那么这两条直线也互相平行.即:a∥b,c∥b,那么a∥c 性质1:过一点有且只有一条直线与已知直线垂直;性质2:直线外一点与直线上各点连结的所有线段中,垂线段最短,简称:垂线段最短.
画法 方格纸 水平、垂直和斜画三种方式 水平、垂直和斜画三种方式
量角器 量角相等 量900的角
三角版 一落,二靠,三移,四画 一贴 二靠 三画
第三板块:综合运用
(一)有趣的七巧板:
1.七巧板的由来
“七巧板”是我国祖先经过反复改进创造的一项卓越成就,是劳动人民智慧的结晶,是一种巧妙的益智游戏,民间俗称“七巧图”,它是用七块不同形状和大小木板构成图形的游戏,19世纪初,七巧板流传到西方,引起人们广泛流传,并迅速传播,被称为“东方魔板”。
2.七巧板的组成
如图1,七巧板是由2块全等的大等腰三角形①②,2块全等的
小等腰三角形⑥⑦,一块中的等腰三角形③,一个正方形⑤,
一个平行四边形④组成。
3.七巧板的特点
由图1可找出许多等量关系,大家试一试:①的直角边等于⑥的
直角边的2倍或等于⑤的边长加⑦的直角边等等。
它有巧板组成,其中有五块等腰三角形,一块是正方形,一块是平行四边形.
说明(1)我们自己可以制作七巧板;
(2)用七巧板可以拼出多种多样的图形.
(二)图案设计:
以直尺、圆规及三角尺为工具,利用这些工具,应用所学过的平行,垂直,角,圆等知识.动手可以设计出许多具有个性的美丽的图案.
四、思想方法
1.“抽象”的思想方法
几何图形都是由现实事物去其物理性质,而只考虑其形状、大小位置,抽象出来的,这也是解决现实生活中问题的一个途径.
2.“比较”的思想方法
比较是一切理解和思维的基础,恰当地运用比较,可以深刻理解抽象的几何概念,弄清它们的联系与区别,所谓比较,就是“在人脑中 把各种事物或现象加以对比,来确定他们之间异同点和关系的思维过程”,例如:在学习直线、线段、射线这三 概念时,可比较他们的异同点.
3.分类思想
分类是解答数学问题常用的思想方法,分类必须按同一标准进行,而且要做到不重复,不遗漏.
4.归纳思想
由简单事物的性质,总结规律,推出复杂事物的性质,这种思维方法称为归纳法.
5.转化思想
解决一个问题,往往是由未知向已知转化,由陌生向熟悉转化,由复杂向简单转化,转化的思想贯穿数学的始终,例如,在求线段的长度或角的度数时,常常运用代数的方法来求解,这里就用了转化思想.
还有方程思想、整体思想、数形结合的思想方法等等,希望同学们在学习时,注意理解和运用.
五、热点、考点透视
热点一:直线公理的运用
例1.一般来说,把门安装在门框上需要两个合页,这是为什么呢?
分析:无论是开门还是关门,都需要门以固定的一直线为轴旋转.
答:是因为经过两点有一条直线且只有一条直线.
热点透视二:线段公理的运用
例2.(1)如图2,从教室门A到图书馆B,总有少数同学不走边上的路而横穿草坪,这是为什么?请你用所学的数学知识来说明这个问题.
(2)如图3,A、B是河流L两旁的两个村庄,现在要在河边修一个引水站向两村供水,
问引水站修在什么地方才能使所需要的管道最短?请在图中表示出点P的位置,并说明你的理由.
(3)你赞同以上的做法吗?为什么?
分析:利用“两点之间,线段最短”.
答:(1)学生从草地穿行是为了少走路,
利用的是两点之间,线段最短.
(2)连接A、B两点与L相交,交点就是P的位置,根据两点之间,线段最短.
(3)第一种做法不对,践踏草坪不道德;第二种做法对,节省物质.
热点透视三:角的实际应用
1.方位角问题
例3.某货轮从A港出发,先沿东北方向(北偏东45°)行驶50km,
再沿北偏西30 °方向行驶35km,然后沿南偏西47°方向行驶35km,到达目的地,
问目的地在A港什么方向
分析:这是生活中的方向角的问题,解决这类问题,只要分清方向,正确地
画出图形,问题便会迎刃而解了
解:如答图4,D点为目的地 D点在A港的北偏西11°.
2.学具拼角题
例4.一副三角板由一个等腰三角形和一个含30°角的直角三角形组成, 利用这副三角板构成15°角的方法很多,请你画出其中三种不同构成的示意图,并在图上作出必要的标注,不写作法.
分析:三角板是同学们常见、常用、必须的学具,它的角应用非常大,用它可以拼出许多角
解:如答图5所示:
评注:三角板拼图与三角板的平移、旋转等问题是近年来中考的热点问题,本题只是三角板的简单应用,只要同学们认真地拼摆,问题就很容易得到解决.
热点透视四:规律探索
例5.问题:在直线上有n个不同点,则此直线上共有多少条线段?
分析:本题属于规律探索题,只要同学们从简单的几种情形入手,就能归纳出一般规律来,即从特殊到一般的思想方法.
解:通过画图尝试,得结论.
当直线上有两点时,有1条线段。
当直线上有三点时,有3条线段,即1+2=3=
(3) 当直线上有四点时,有6条线段,即1+2+3=6=
(4) 当直线上有五点时,有10条线段,即1+2+3+4=10=
∴当直线上有n点时,有1+2+3+4+…+n=条线段.
评注:我们把这种“数线段”的规律称为“数线段模型”。它在解数学题时意义非常重大,在我们生活中也有着重要的应用(详见专题辅导内容:《铸题成模 以模解题》).
热点透视五:网格操作
例6.如图6,在方格纸上有一条线段AB和一点C.
①过点C画出与AB平行的直线;
②过点C画出与AB垂直的直线.
分析:作平行线时,要找矩形、对角线的规律完全相同;而作垂线时,却不同,AB所在的矩形是一行三列,则它的垂线所在矩形应是三行一列,AB是矩形中从左上到右下的对角线,则它的垂线应是所在矩形中从右上到左下的对角线.
答案:如图7:
评注:在网格内画平行、垂直重点考查学生的动手操作能力、
空间想象能力等综合能力,这也是新课标所倡导的.
热点透视六:七巧板趣题
例7.如图8,用一块边长为2的正方形ABCD厚纸板,按照下面的作法,做了一套七巧板:作对角线AC,分别取AB、BC中点E、F,连结EF;作DG⊥EF于G,交AC于H;过G作GL∥BC,交AC于L,再由E作EK∥DG,交AC于K;将正方形ABCD沿画出的线剪开,现用它拼出一座桥(如图9),这座桥的阴影部分的面积是( )
A.8 B.6 C.4 D.5
分析:本题先将正方形割成七巧板,然后再拼成一座桥,因此不难发现阴影部分是由5个小板构成的,由于拼图前后图形的总面积以及7个小板的面积不变,所以这座桥的阴影部分的面积应是正方形面积的一半,即阴影部分的面积为4,故选C.
例8.(1)在七巧板中(如图8),找几组平行线或垂直的线段?
(2)在七巧板中(如图8),直角、锐角、钝角有哪些?
分析:根据七巧板中每个图形的特点可以得到:
(1)平行线有:AB∥DC;EK∥HG;LG∥CF等;
垂直的线段有:EK⊥AC;GH⊥AC;EG⊥HG等
(2)锐角12个:∠BAH;∠FGL;∠HGL等,它们均为450
直角有:∠AHG;∠HKE;∠LHG;∠KEG等;
钝角有:∠CLG;∠CFG,它们均内为1350
评注:平常我们熟悉的许多玩具(如七巧板等)及游戏活动中常常包含着许多与数学有关的知识.智力游戏型探究题具有寓教于乐、开发智力、激活思维,培养动手实践、自主探索能力及良好的学习习惯,如本题中就包含着许多线、角之间的关系.
巩固练习:
1、 小明由A点出发向正东方向走10米到达B点,再由B点向东南方向走10米到达C点,则正确的是( D )
A.∠ABC=22.5° B.∠ABC=45°
C.∠ABC=67.5° D.∠ABC=135°
3、如图,一条街道旁有五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( C )
4、一艘轮船由海平面上A地出发向南偏西40 的方向行驶40海里到达B地,再由B地向北偏西10 的方向行驶40海里到达C地,则A、C两地相距( B ).
(A)30海里 (B)40海里 (C)50海里 (D)60海里
5、 如图,小明在操场上从A点出发,沿直线前进10米后向左转40o,再沿直线前进10米后,又向左转40o,照这样走下去,他第一次回到出发地A点时,一共走了 90 米.
综合应用
(七巧板、图案设计)
角的比较
平行
垂直
线段的比较
符号表示
大小关系
位置关系
平面图形
线段、射线和直线
角
符号表示
大小关系
a
B
A
M
O
l
B
A
·
A
·
C
·
B
A
O
C
B
②
④
⑦
①
⑤
⑥
③
图1
B
A
L
图3
教学楼
草地
图书馆
图2
图4
图5
图6
图7
图9
图8
北
北
A
B
C
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《几何图形初步》复习指导
一、课标要求
1.经历观察、测量、折纸、剪切、模型制作,拼摆与简单图案设计等活动过程.发展空间观念.
2.在现实情境中认识线段、射线、直线、角等简单平面图形,了解平面上两条直线的平行和垂直关系.
3.能用字母表示角、线段、互相平行或垂直的直线.
4.会进行线段或角的比较,能估计一个角的大小,会进行有关角度的换算.活动中探索图形性质的过程,了解线段、平行、垂直的有关性质,丰富数学学习的体验,积累操作活动经验,发展有条理地思考与表达.
5.掌握借助三角尺、量角器、方格纸画角、线段、平行线、垂线的简便方法,能进行简单的图案设计,并能表达和交流自己的设计方案.
二、知识结构
在本章中,我们不仅能从测量、折纸、画图等活动中学到线段、直线、射线、角等简单的平面图形,以及两直线平行、垂直的位置关系和特征,而且还可以自己创作出新颖、有趣的七巧板拼图,用尺规设计出精美、别致的图案,这样,你自己也会成为一名小小的设计师,更会感受到美就在我们身边.本章的知识结构归纳为:
三、要点扫描
本章的要点内容共分“三大板块”
第一板块:线、角的特性
1.线段、射线、直线三者之间的联系与区别,共性与特性
线段 射线 直线
图形
表示方法 线段AB、线段a 射线OM 直线AB、直线l
端点 2个 1个 无
共性 线段、射线、直线都是笔直的.
特性 线段有两个端点,不向任何一旁延伸,可以度量;射线有一个端点,向一旁无限延伸,不能度量;直线没有端点,向两旁无限延伸,不能度量.
联系 射线和线段都是直线的一部分.
2.线段、角的有关知识对比
线段 角
定义 直线上两点之间的部分 1)有公共端点的两条射线组成的图形叫角。这个公共端点叫做角的顶点,两条射线叫做角的边.2)角也可以看成是一条射线绕着端点从起始位置旋转到终止位置所组成的图形.
表示 两种:两个大写英文字母、一个小写英文字母 四种:三个大写英文字母;一个大写英文字母;一个阿拉伯数字;一个小写希腊字母
比较 (1)叠合法(2)度量法 (1)叠合法(2)度量法
度量 (1)测量工具:刻度尺(2)换算:1km=1000m,1m=10dm,1dm=10cm,1cm=10mm (1)测量工具:量角器(2)换算:1周角=2平角=4直角,1平角=2直角,1 =60',1'=60"
和差的表示 (1)和:AC+BC=AB(2)差:AB-AC=BCAB-BC=AC (1)和:∠AOC+∠BOC=∠AOB(2)差:∠AOB-∠AOC=∠BOC
等分点(线) 线段的中点、三等分点等 角的平分线、三等分线等
其他 1.直线的基本性质:两点确定一条直线2.线段的基本性质:两点之间,线段最短3.两点之间的距离:两点之间的线段的长度 角的分类:周角、平角、钝角、直角、锐角
第二板块:平行与垂直
在同一平面,两条直线的位置关系只有两种:①相交 ②平行.
平行 垂直
定义 在同一平面内,不相交的两条直线叫做平行线 当两条直线相交成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫垂足
表示 用符号“∥”表示 用符号“⊥”表示
性质 性质1:经过直线外一点,有且只有一条直线与已知直线平行.性质2(传递性):如果两条直线都和第三条直线平行,那么这两条直线也互相平行.即:a∥b,c∥b,那么a∥c 性质1:过一点有且只有一条直线与已知直线垂直;性质2:直线外一点与直线上各点连结的所有线段中,垂线段最短,简称:垂线段最短.
画法 方格纸 水平、垂直和斜画三种方式 水平、垂直和斜画三种方式
量角器 量角相等 量900的角
三角版 一落,二靠,三移,四画 一贴 二靠 三画
第三板块:综合运用
(一)有趣的七巧板:
1.七巧板的由来
“七巧板”是我国祖先经过反复改进创造的一项卓越成就,是劳动人民智慧的结晶,是一种巧妙的益智游戏,民间俗称“七巧图”,它是用七块不同形状和大小木板构成图形的游戏,19世纪初,七巧板流传到西方,引起人们广泛流传,并迅速传播,被称为“东方魔板”。
2.七巧板的组成
如图1,七巧板是由2块全等的大等腰三角形①②,2块全等的
小等腰三角形⑥⑦,一块中的等腰三角形③,一个正方形⑤,
一个平行四边形④组成。
3.七巧板的特点
由图1可找出许多等量关系,大家试一试:①的直角边等于⑥的
直角边的2倍或等于⑤的边长加⑦的直角边等等。
它有巧板组成,其中有五块等腰三角形,一块是正方形,一块是平行四边形.
说明(1)我们自己可以制作七巧板;
(2)用七巧板可以拼出多种多样的图形.
(二)图案设计:
以直尺、圆规及三角尺为工具,利用这些工具,应用所学过的平行,垂直,角,圆等知识.动手可以设计出许多具有个性的美丽的图案.
四、思想方法
1.“抽象”的思想方法
几何图形都是由现实事物去其物理性质,而只考虑其形状、大小位置,抽象出来的,这也是解决现实生活中问题的一个途径.
2.“比较”的思想方法
比较是一切理解和思维的基础,恰当地运用比较,可以深刻理解抽象的几何概念,弄清它们的联系与区别,所谓比较,就是“在人脑中 把各种事物或现象加以对比,来确定他们之间异同点和关系的思维过程”,例如:在学习直线、线段、射线这三 概念时,可比较他们的异同点.
3.分类思想
分类是解答数学问题常用的思想方法,分类必须按同一标准进行,而且要做到不重复,不遗漏.
4.归纳思想
由简单事物的性质,总结规律,推出复杂事物的性质,这种思维方法称为归纳法.
5.转化思想
解决一个问题,往往是由未知向已知转化,由陌生向熟悉转化,由复杂向简单转化,转化的思想贯穿数学的始终,例如,在求线段的长度或角的度数时,常常运用代数的方法来求解,这里就用了转化思想.
还有方程思想、整体思想、数形结合的思想方法等等,希望同学们在学习时,注意理解和运用.
五、热点、考点透视
热点一:直线公理的运用
例1.一般来说,把门安装在门框上需要两个合页,这是为什么呢?
分析:无论是开门还是关门,都需要门以固定的一直线为轴旋转.
答:是因为经过两点有一条直线且只有一条直线.
热点透视二:线段公理的运用
例2.(1)如图2,从教室门A到图书馆B,总有少数同学不走边上的路而横穿草坪,这是为什么?请你用所学的数学知识来说明这个问题.
(2)如图3,A、B是河流L两旁的两个村庄,现在要在河边修一个引水站向两村供水,
问引水站修在什么地方才能使所需要的管道最短?请在图中表示出点P的位置,并说明你的理由.
(3)你赞同以上的做法吗?为什么?
分析:利用“两点之间,线段最短”.
答:(1)学生从草地穿行是为了少走路,
利用的是两点之间,线段最短.
(2)连接A、B两点与L相交,交点就是P的位置,根据两点之间,线段最短.
(3)第一种做法不对,践踏草坪不道德;第二种做法对,节省物质.
热点透视三:角的实际应用
1.方位角问题
例3.某货轮从A港出发,先沿东北方向(北偏东45°)行驶50km,
再沿北偏西30 °方向行驶35km,然后沿南偏西47°方向行驶35km,到达目的地,
问目的地在A港什么方向
分析:这是生活中的方向角的问题,解决这类问题,只要分清方向,正确地
画出图形,问题便会迎刃而解了
解:如答图4,D点为目的地 D点在A港的北偏西11°.
2.学具拼角题
例4.一副三角板由一个等腰三角形和一个含30°角的直角三角形组成, 利用这副三角板构成15°角的方法很多,请你画出其中三种不同构成的示意图,并在图上作出必要的标注,不写作法.
分析:三角板是同学们常见、常用、必须的学具,它的角应用非常大,用它可以拼出许多角
解:如答图5所示:
评注:三角板拼图与三角板的平移、旋转等问题是近年来中考的热点问题,本题只是三角板的简单应用,只要同学们认真地拼摆,问题就很容易得到解决.
热点透视四:规律探索
例5.问题:在直线上有n个不同点,则此直线上共有多少条线段?
分析:本题属于规律探索题,只要同学们从简单的几种情形入手,就能归纳出一般规律来,即从特殊到一般的思想方法.
解:通过画图尝试,得结论.
当直线上有两点时,有1条线段。
当直线上有三点时,有3条线段,即1+2=3=
(3) 当直线上有四点时,有6条线段,即1+2+3=6=
(4) 当直线上有五点时,有10条线段,即1+2+3+4=10=
∴当直线上有n点时,有1+2+3+4+…+n=条线段.
评注:我们把这种“数线段”的规律称为“数线段模型”。它在解数学题时意义非常重大,在我们生活中也有着重要的应用(详见专题辅导内容:《铸题成模 以模解题》).
热点透视五:网格操作
例6.如图6,在方格纸上有一条线段AB和一点C.
①过点C画出与AB平行的直线;
②过点C画出与AB垂直的直线.
分析:作平行线时,要找矩形、对角线的规律完全相同;而作垂线时,却不同,AB所在的矩形是一行三列,则它的垂线所在矩形应是三行一列,AB是矩形中从左上到右下的对角线,则它的垂线应是所在矩形中从右上到左下的对角线.
答案:如图7:
评注:在网格内画平行、垂直重点考查学生的动手操作能力、
空间想象能力等综合能力,这也是新课标所倡导的.
热点透视六:七巧板趣题
例7.如图8,用一块边长为2的正方形ABCD厚纸板,按照下面的作法,做了一套七巧板:作对角线AC,分别取AB、BC中点E、F,连结EF;作DG⊥EF于G,交AC于H;过G作GL∥BC,交AC于L,再由E作EK∥DG,交AC于K;将正方形ABCD沿画出的线剪开,现用它拼出一座桥(如图9),这座桥的阴影部分的面积是( )
A.8 B.6 C.4 D.5
分析:本题先将正方形割成七巧板,然后再拼成一座桥,因此不难发现阴影部分是由5个小板构成的,由于拼图前后图形的总面积以及7个小板的面积不变,所以这座桥的阴影部分的面积应是正方形面积的一半,即阴影部分的面积为4,故选C.
例8.(1)在七巧板中(如图8),找几组平行线或垂直的线段?
(2)在七巧板中(如图8),直角、锐角、钝角有哪些?
分析:根据七巧板中每个图形的特点可以得到:
(1)平行线有:AB∥DC;EK∥HG;LG∥CF等;
垂直的线段有:EK⊥AC;GH⊥AC;EG⊥HG等
(2)锐角12个:∠BAH;∠FGL;∠HGL等,它们均为450
直角有:∠AHG;∠HKE;∠LHG;∠KEG等;
钝角有:∠CLG;∠CFG,它们均内为1350
评注:平常我们熟悉的许多玩具(如七巧板等)及游戏活动中常常包含着许多与数学有关的知识.智力游戏型探究题具有寓教于乐、开发智力、激活思维,培养动手实践、自主探索能力及良好的学习习惯,如本题中就包含着许多线、角之间的关系.
巩固练习:
1、 小明由A点出发向正东方向走10米到达B点,再由B点向东南方向走10米到达C点,则正确的是( D )
A.∠ABC=22.5° B.∠ABC=45°
C.∠ABC=67.5° D.∠ABC=135°
3、如图,一条街道旁有五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( C )
4、一艘轮船由海平面上A地出发向南偏西40 的方向行驶40海里到达B地,再由B地向北偏西10 的方向行驶40海里到达C地,则A、C两地相距( B ).
(A)30海里 (B)40海里 (C)50海里 (D)60海里
5、 如图,小明在操场上从A点出发,沿直线前进10米后向左转40o,再沿直线前进10米后,又向左转40o,照这样走下去,他第一次回到出发地A点时,一共走了 90 米.
综合应用
(七巧板、图案设计)
角的比较
平行
垂直
线段的比较
符号表示
大小关系
位置关系
平面图形
线段、射线和直线
角
符号表示
大小关系
a
B
A
M
O
l
B
A
·
A
·
C
·
B
A
O
C
B
②
④
⑦
①
⑤
⑥
③
图1
B
A
L
图3
教学楼
草地
图书馆
图2
图4
图5
图6
图7
图9
图8
北
北
A
B
C
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
