数学高中北师大版必修五1.3《等比数列》课件
文档属性
| 名称 | 数学高中北师大版必修五1.3《等比数列》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 00:00:00 | ||
图片预览











文档简介
课件30张PPT。北师大版高中数学必修5第一章《数列》SnSn=?an-an-1=d(n≥2)(n≥2)an=a1+(n-1)d
an=am+(n-m)dan=a1·qn-1(q≠0)
an=am·qn-mA=G=若m+n=p+q,则
am+an=ap+aq若m+n=p+q,则aman=apaq问题提出 小林和小明做“贷款”游戏,规定:在一月(30天)中小明
第一天贷给小林1万元,第二天贷给小林2万元……以后每天比前
一天多贷1万元.而小林按这样方式还贷:第一天支付1分钱,第二
天还2分钱,第三天还4分钱……以后每天还的钱是前一天的2倍,
試计算30天后两人各得的钱数.设小林30天得到的钱数T30设小明30天得到的钱数S 30引入新课同学们考虑如何求出这个和?≈1073.741万元这种求和的方法,就是错位相减法!推导公式等比数列前n项求和公式解:Sn=a1+a2 + a3 +a4 + …+an
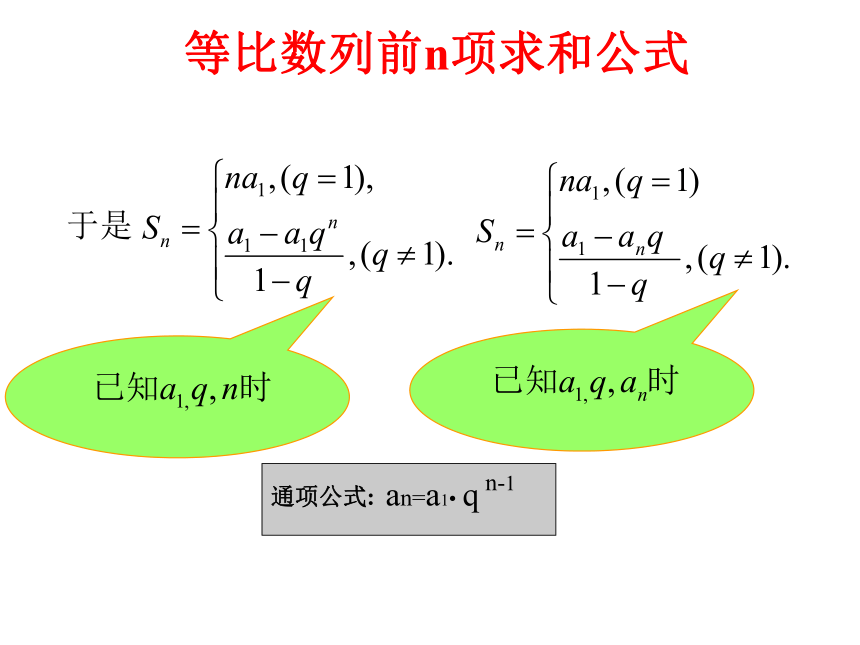
qsn=若:q≠1若q=1,6(一) 用等比定理推导当 q = 1 时 Sn = n a1因为所以7Sn = a1 + a2 + a3 + …….+ an-1 + an = a1 + a1q + a1q2 +…..+ a1qn-2 + a1qn-1= a1+ q ( a1 + a1q + ….+ a1qn-3 + a1qn-2 )= a1 + q Sn-1 = a1 + q ( Sn – an )(二)公式推导于是等比数列前n项求和公式等比数列的前n项和例题解: 例5(1) 求等比数列 的前10项的和.(2)已知等比数列{an}中,a1=2,q=3,求S3例6 五洲电扇厂去年实现利税300万元,
计划在5年中每年比上年利税增长10%,
问从今年起第5年的利税是多少?这5年
的总利税是多少?(结果精确到万元)等比数列的前n项和例题等比数列的前n项和练习11. 根据下列条件,求相应的等比数列 的等比数列的前n项和练习2-32. 求等比数列 1,2,4,…从第5项到第10项的和. 从第5项到第10项的和: 3. 求等比数列 从第3项到第7项的和. 从第3项到第7项的和:作业:P30.A组8(写在课本)9.10(写在作业本)152、求数列1,x,x2,x3,…,xn,…的前n项和。1、等比数列1,2,4,8,…从第5项到
第10项的和为或3、求和:北师大版高中数学必修5第一章《数列》(2)(1)(3)若数列 是等比数列,则
也是等比数列 (4)等比数列{an}的任意等距离的项
构成的数列仍为等比数列等比数列判定方法:
(1)定义法:
(2)递推公式法:
(3)看通项法:
(4)看前n项和法:例 一个热气球在第一分钟上升了25m的高度,在以
后的每一分钟里,它上升的高度,都是它在前一分钟
上升高度的80%.这个热气球上升的高度能超过125m吗?解 用an表示热气球在第n分钟上升的高度,由题意,
得 an+1=4/5an因此,数列{an}是首项a1=25,公比q=4/5的等比数列热气球在n分时间里上升的总高度
例 做边长为a的正三角形的内切圆,在这个圆内做内
接正三角形,然后再做新三角形的内切圆.如此下去求
前n个内切圆的面积和.解 设第n个正三角形的内切圆的半径为rn
从第二个三角形开始,每一个正三角形的边长是前一个
正三角形边长的1/2,每一个正三角形内切圆的半径也是
前一个正三角形内切圆半径的1/2,故设前n个内切圆的面积之和为Sn,则:练习3:一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项解:设这个等比数列的第1项是 ,公比是 ,那么答:这个数列的第1项与第2项分别为 与 8消元练习、求和分析:公比是字母,分 q=1 和 q≠1两种情况讨论解:(1)该数列为等比数列,记为{an},其中a1=a,q=a当q=1时,Sn=na当q≠1时,Sn=(1)如果一个等比数列前5项的和等于10,前10项的和等于50,那么它前15项的和等于多少?练习:思考:求和: .2.灵活运用等比数列求和公式进行求和,求和时注意公比q课堂小结:课本p31习题1-3 B组2、3. 4?布置作业:
an=am+(n-m)dan=a1·qn-1(q≠0)
an=am·qn-mA=G=若m+n=p+q,则
am+an=ap+aq若m+n=p+q,则aman=apaq问题提出 小林和小明做“贷款”游戏,规定:在一月(30天)中小明
第一天贷给小林1万元,第二天贷给小林2万元……以后每天比前
一天多贷1万元.而小林按这样方式还贷:第一天支付1分钱,第二
天还2分钱,第三天还4分钱……以后每天还的钱是前一天的2倍,
試计算30天后两人各得的钱数.设小林30天得到的钱数T30设小明30天得到的钱数S 30引入新课同学们考虑如何求出这个和?≈1073.741万元这种求和的方法,就是错位相减法!推导公式等比数列前n项求和公式解:Sn=a1+a2 + a3 +a4 + …+an
qsn=若:q≠1若q=1,6(一) 用等比定理推导当 q = 1 时 Sn = n a1因为所以7Sn = a1 + a2 + a3 + …….+ an-1 + an = a1 + a1q + a1q2 +…..+ a1qn-2 + a1qn-1= a1+ q ( a1 + a1q + ….+ a1qn-3 + a1qn-2 )= a1 + q Sn-1 = a1 + q ( Sn – an )(二)公式推导于是等比数列前n项求和公式等比数列的前n项和例题解: 例5(1) 求等比数列 的前10项的和.(2)已知等比数列{an}中,a1=2,q=3,求S3例6 五洲电扇厂去年实现利税300万元,
计划在5年中每年比上年利税增长10%,
问从今年起第5年的利税是多少?这5年
的总利税是多少?(结果精确到万元)等比数列的前n项和例题等比数列的前n项和练习11. 根据下列条件,求相应的等比数列 的等比数列的前n项和练习2-32. 求等比数列 1,2,4,…从第5项到第10项的和. 从第5项到第10项的和: 3. 求等比数列 从第3项到第7项的和. 从第3项到第7项的和:作业:P30.A组8(写在课本)9.10(写在作业本)152、求数列1,x,x2,x3,…,xn,…的前n项和。1、等比数列1,2,4,8,…从第5项到
第10项的和为或3、求和:北师大版高中数学必修5第一章《数列》(2)(1)(3)若数列 是等比数列,则
也是等比数列 (4)等比数列{an}的任意等距离的项
构成的数列仍为等比数列等比数列判定方法:
(1)定义法:
(2)递推公式法:
(3)看通项法:
(4)看前n项和法:例 一个热气球在第一分钟上升了25m的高度,在以
后的每一分钟里,它上升的高度,都是它在前一分钟
上升高度的80%.这个热气球上升的高度能超过125m吗?解 用an表示热气球在第n分钟上升的高度,由题意,
得 an+1=4/5an因此,数列{an}是首项a1=25,公比q=4/5的等比数列热气球在n分时间里上升的总高度
例 做边长为a的正三角形的内切圆,在这个圆内做内
接正三角形,然后再做新三角形的内切圆.如此下去求
前n个内切圆的面积和.解 设第n个正三角形的内切圆的半径为rn
从第二个三角形开始,每一个正三角形的边长是前一个
正三角形边长的1/2,每一个正三角形内切圆的半径也是
前一个正三角形内切圆半径的1/2,故设前n个内切圆的面积之和为Sn,则:练习3:一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项解:设这个等比数列的第1项是 ,公比是 ,那么答:这个数列的第1项与第2项分别为 与 8消元练习、求和分析:公比是字母,分 q=1 和 q≠1两种情况讨论解:(1)该数列为等比数列,记为{an},其中a1=a,q=a当q=1时,Sn=na当q≠1时,Sn=(1)如果一个等比数列前5项的和等于10,前10项的和等于50,那么它前15项的和等于多少?练习:思考:求和: .2.灵活运用等比数列求和公式进行求和,求和时注意公比q课堂小结:课本p31习题1-3 B组2、3. 4?布置作业:
