数学高中北师大版必修五3.2《一元二次不等式》课件1
文档属性
| 名称 | 数学高中北师大版必修五3.2《一元二次不等式》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 364.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 00:00:00 | ||
图片预览





文档简介
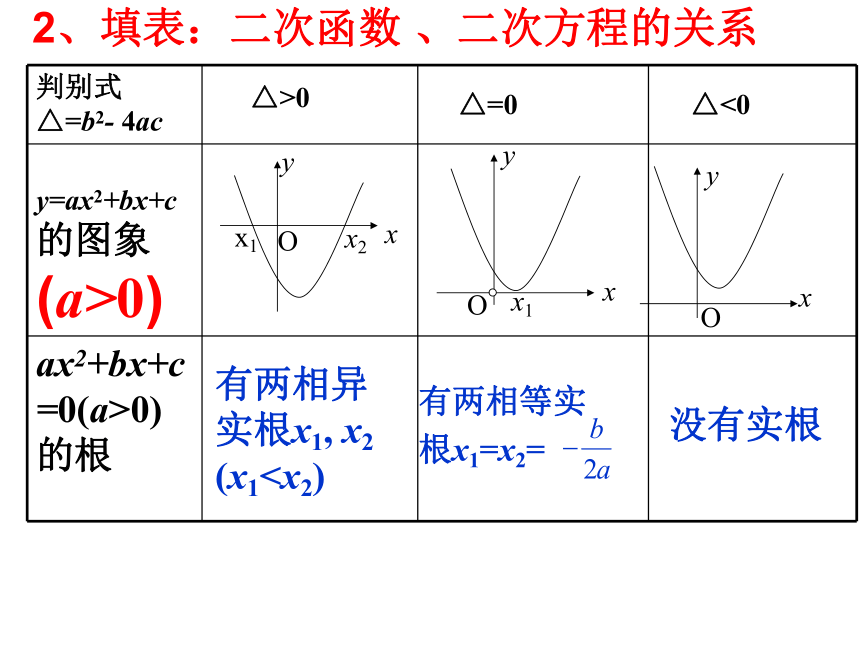
课件19张PPT。复习:一元二次方程与一元二次函数因式分解法(十字相乘)公式法:韦达定理开口方向;对称轴顶点 坐标△>0有两相异实根x1, x2 (x10 和 3x2+6x-1≤0.这两个不等式有两个共同特点: (1)含有一个未知数x;
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。导入新课 一元二次不等式的一般表达式为 ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)其中a,b,c均为常数。 一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
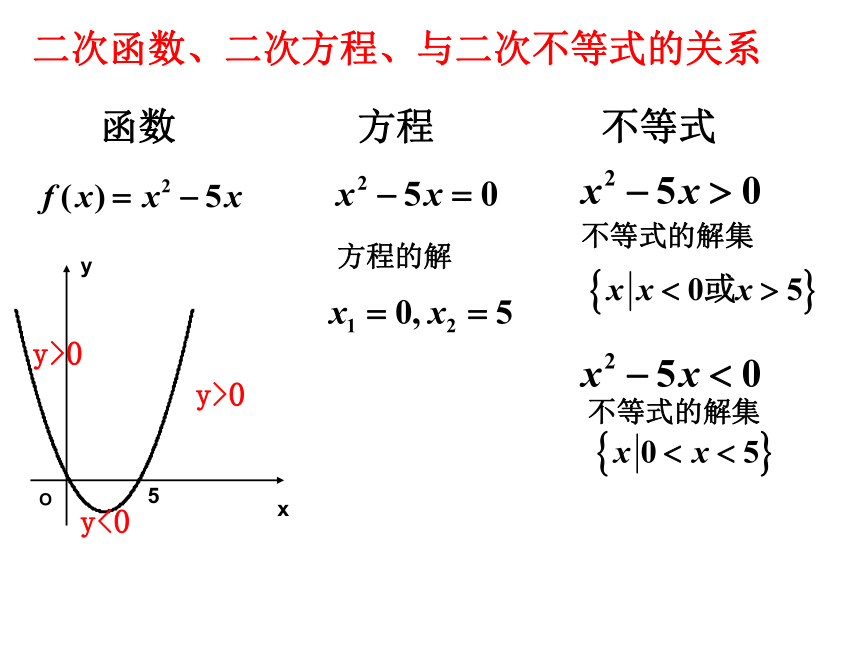
即 f(x)=ax2+bx+c (a≠0), 一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。 一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。 因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。5函数方程不等式方程的解不等式的解集不等式的解集y>0y>0y<0二次函数、二次方程、与二次不等式的关系△>0有两相异实根
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根二次函数 、方程、不等式之间的关系y>0y>0y>0y<0探究1:一元二次不等式的解法,并完成下表计算△,确定方程的根的情况总结一元二次不等式解集的端点就是对应函数的零点,就是对应方程的实根。注意:利用不等式的性质,将不等式的两边同时乘以-1,使二次项系数变为正。探究3、如果不等式为其解集又是怎样的?△>0有两相异实根
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根二次函数 、方程、不等式之间的关系y>0y>0y>0y<0合作探究
RΦ例1:解不等式 2x2-3x-2 > 0 .解:因为△ =(-3)2-4×2×(-2)>0,方程的解2x2-3x-2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状注:开口向上,大于0
解集是大于大根,小于小根(两边飞)应用探究若改为:不等式 2x2-3x-2 < 0 .注:开口向上,小于0
解集是大于小根且小于大根(中间夹)图象为:小结:利用二次函数图象解一元二次不等式其方法步骤是:(2)求出Δ和相应方程的解;(3)再画出函数图象,根据图象写出不等式的解集。(1)先将不等式化为标准形式变式练习:
1、解不等式 4x2-4x+1 > 0 应用探究讨论:(1)4x2-4x+1 <0的解集?Φ2、解不等式 -x2 +2x-3 > 0 (2)x2 -2x+3 >0的解集?R训练评估1、解下列不等式2、求函数
的定义域 作业与思考R-12-2-2≤a≤6作业:习题3.2第1、2、3、4、5题温馨提示不等式的解集一定要书写规范,只能用集合或区间形式表示(2)求出Δ和相应方程的解;(3)再画出函数图象,根据图象写出不等式的解集。2. 二次函数一元二次不等式的解一元二次方程的根图象三个“二次”问题都可以通过图形实现转换1.利用二次函数图象解一元二次不等式的方法步骤知识整理(1)先将不等式化为标准形式3、不等式的解集一定要书写规范,只能用集合或区间形式表示4、数学思想方法类比、数形结合的思想本节课我们学习了哪些知识,运用了哪些数学思想方法?谢谢大家,再见!敬请多提宝贵意见!
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。导入新课 一元二次不等式的一般表达式为 ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)其中a,b,c均为常数。 一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
即 f(x)=ax2+bx+c (a≠0), 一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。 一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。 因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。5函数方程不等式方程的解不等式的解集不等式的解集y>0y>0y<0二次函数、二次方程、与二次不等式的关系△>0有两相异实根
x1, x2 (x1
x1, x2 (x1
RΦ例1:解不等式 2x2-3x-2 > 0 .解:因为△ =(-3)2-4×2×(-2)>0,方程的解2x2-3x-2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状注:开口向上,大于0
解集是大于大根,小于小根(两边飞)应用探究若改为:不等式 2x2-3x-2 < 0 .注:开口向上,小于0
解集是大于小根且小于大根(中间夹)图象为:小结:利用二次函数图象解一元二次不等式其方法步骤是:(2)求出Δ和相应方程的解;(3)再画出函数图象,根据图象写出不等式的解集。(1)先将不等式化为标准形式变式练习:
1、解不等式 4x2-4x+1 > 0 应用探究讨论:(1)4x2-4x+1 <0的解集?Φ2、解不等式 -x2 +2x-3 > 0 (2)x2 -2x+3 >0的解集?R训练评估1、解下列不等式2、求函数
的定义域 作业与思考R-12-2-2≤a≤6作业:习题3.2第1、2、3、4、5题温馨提示不等式的解集一定要书写规范,只能用集合或区间形式表示(2)求出Δ和相应方程的解;(3)再画出函数图象,根据图象写出不等式的解集。2. 二次函数一元二次不等式的解一元二次方程的根图象三个“二次”问题都可以通过图形实现转换1.利用二次函数图象解一元二次不等式的方法步骤知识整理(1)先将不等式化为标准形式3、不等式的解集一定要书写规范,只能用集合或区间形式表示4、数学思想方法类比、数形结合的思想本节课我们学习了哪些知识,运用了哪些数学思想方法?谢谢大家,再见!敬请多提宝贵意见!
