数学高中北师大版必修五3.3《基本不等式》课件
文档属性
| 名称 | 数学高中北师大版必修五3.3《基本不等式》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 00:00:00 | ||
图片预览








文档简介
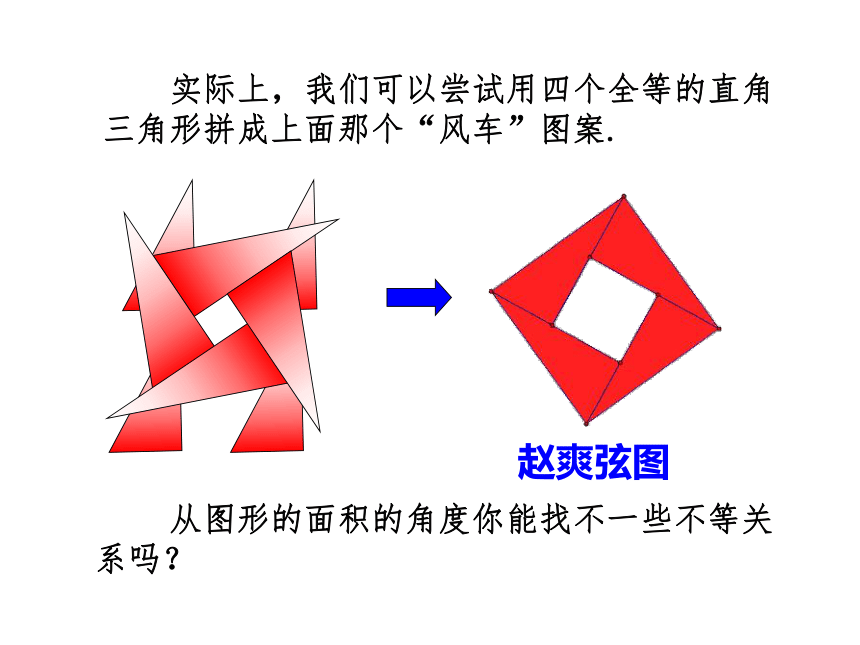
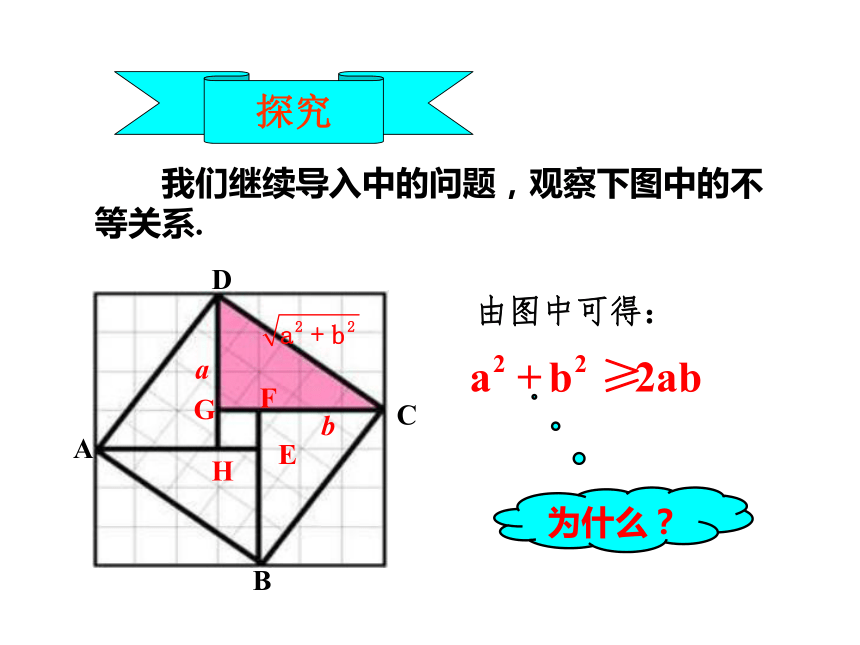
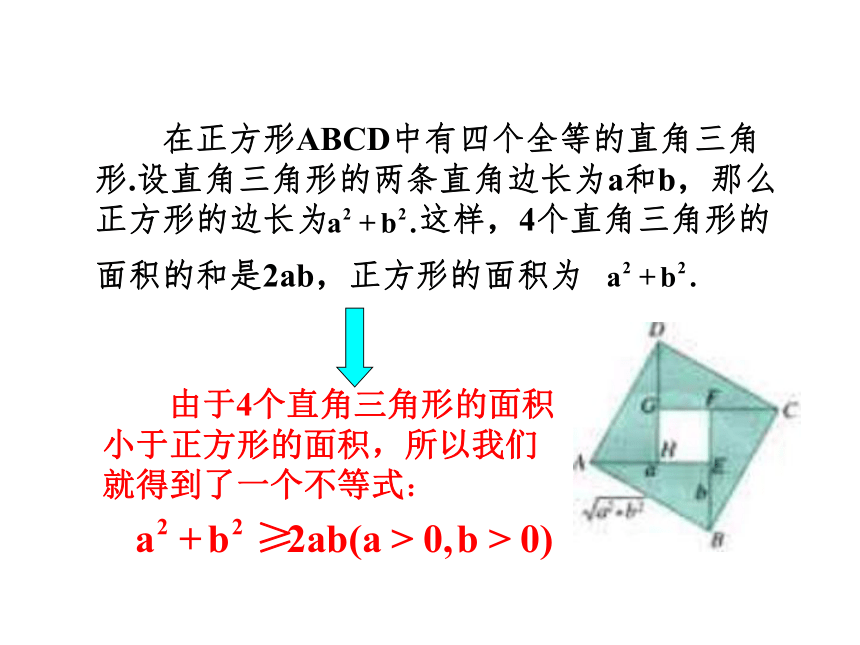
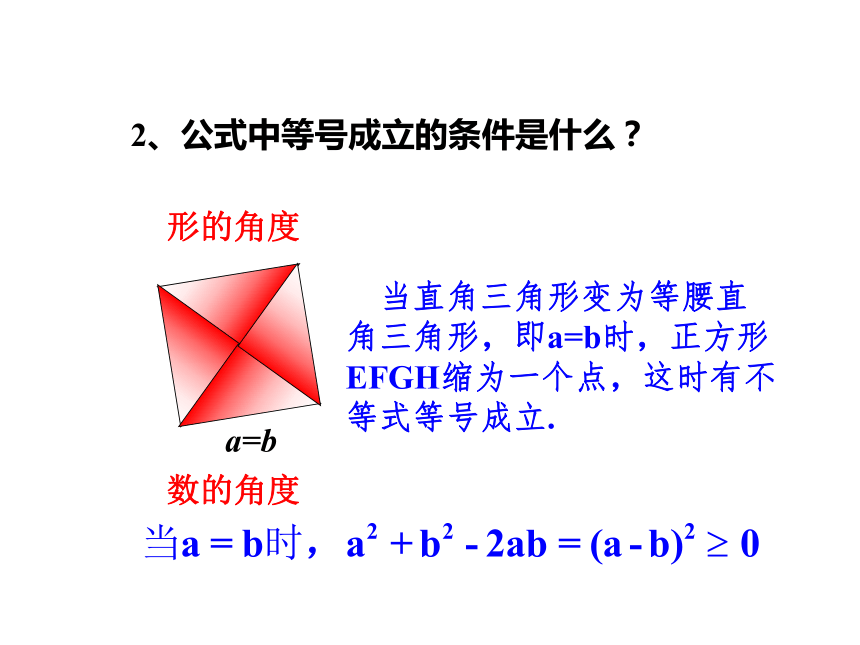
课件43张PPT。新课导入 如图是在北京召开的第24界国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车。你能在这个图案中找出一些相等关系或不等关系吗?基本不等式的几何背景. 实际上,我们可以尝试用四个全等的直角三角形拼成上面那个“风车”图案.赵爽弦图 从图形的面积的角度你能找不一些不等关系吗?3.4基本不等式教学目标知识与能力 1.学会推导并掌握基本不等式,理解这个基本不等式的几何意义,并掌握定理中的不等号“≥”取等号的条件是:当且仅当这两个数相等; 2.进一步掌握基本不等式 会应用此不等式求某些函数的最值;能够解决一些简单的实际问题.1.通过实例探究抽象基本不等式; 过程与方法 2.通过几个例题的研究,进一步掌握基本不等式并会用此定理求某些函数的最大、最小值; 3.会利用基本不等式证明一些比较简单的证明题,从而从基本不等式中衍生新的结论. 1.通过本节的学习,体会数学来源于生活,提高学习数学的兴趣; 情感态度与价值观 2.引发学生学习和使用数学知识的兴趣,发展创新精神,培养实事求是、理论与实际相结合的科学态度和科学道德; 3.积极倡导同学们进行几何与代数的结合运用,发现各种事物之间的普遍联系.重点难点教学重难点 1.应用数形结合的思想理解不等式,并从不同角度探索基本不等式的证明过程; 2.掌握基本不等式,会用此不等式证明不等式,会用此不等式求某些函数的最值.1.基本不等式等号成立条件;2.利用此不等式求函数的最大、最小值.探究 我们继续导入中的问题,观察下图中的不等关系.由图中可得:为什么? 在正方形ABCD中有四个全等的直角三角形.设直角三角形的两条直角边长为a和b,那么正方形的边长为 这样,4个直角三角形的 由于4个直角三角形的面积小于正方形的面积,所以我们就得到了一个不等式:面积的和是2ab,正方形的面积为 思考:1、不等式在什么条件下都成立吗?形的角度a>0,b>0数的角度从而,a和b是实数时,不等式都成立.2、公式中等号成立的条件是什么?形的角度数的角度a=b 当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有不等式等号成立.3、公式两边具有何种运算结构?数的角度:平方和不小于积的2倍 小结:由上面的讨论,我们得到一个结论:(当且仅当a=b时,等号成立) 引申1、认识基本不等式特别的,如果a>0,b>0,我们用去代替a和b,可得通常我们把上式写成(当且仅当a=b时取等号)从而我们得到了这个基本不等式.2、从不等式的性质推导基本不等式的性质. 分析:我们从几何图形中的关系获得了基本不等式,能否利用不等式的性质,直接推导出这个不等式呢?要证(2),只要证 要证 (1)只要证 显然,(4)是成立的。当且仅当a=b时, (4)中的等号成立. 3、这样,我们又一次的得到了基本不等式 分析法即为,之前证明基本不等式时用的以结论来推过程的方法.小结: 1、经过以上的引申,我们得到了一个基本不等式2、我们应熟练掌握分析法证明不等式.是什么?思考: 我们之前用分析法证明了基本不等式,它有什么几何意义吗? 在右图中,AB是圆的直径,点C是AB上的一点,AC=a,BC=b.过点C作垂直于AB的弦DE,连接AD、BD. 根据圆的性质,我们知道:半径不小于半弦从而得到:概念1、如果把 看作是正数a、b的等差中项, 看作是正数a、b的等比中项,那么该定理可以叙述为:两个正数的等差中项不小于它们的等比中项. 2、在数学中,我们称 为a、b的算术平均数 ,称 为a、b的几何平均数.本节定理还可叙述为:两个正数的算术平均数不小于它们的几何平均数.实际问题 1、用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短篱笆是多少? 2、一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大.最大面积是多少? 分析:对于(1),矩形菜园的面积是确定的.因此我们要解决的问题是:当面积确定时,长和宽取什么值时篱笆的周长最短? 对于(2),矩形菜园的周长是确定的,长和宽没有确定.我们要解决的问题是:当周长确定时,长和宽取什么值时篱笆围成的面积越大?解:(1)设矩形菜园的长为x m,宽为y m,则xy=100,篱笆的长为2(x+y) m. 由 可得即x+y≥20,当且仅当x=y=10时等号成立.因此,这个矩形的长、宽都为10m时,所用的篱笆最短,最短的篱笆是40m.(2)解法一:设矩形菜园的宽为x m,则长为(36-2x)m,其中0<x< 其面积S=x(36-2x)= ×2x(36-2x) 当且仅当2x=36-2x,即x=9时菜园面积最大,即菜园长9m,宽为9 m时菜园面积最大为81 m2. 解法二:设矩形菜园的长为x m,宽为y m ,则2(x+y)=36, x+y=18,矩形菜园的面积为xy m2.由可得xy≤81.当且仅当x=y,即x=y=9时,等号成立. 因此,这个矩形的长、宽都为9m时,菜园的面积最大,最大面积是81m2.从上面的实际问题中,你能得到什么结论呢?小结: 1、两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M为定值,则ab等号当且仅当a=b时成立. 2、两个正数的积为定值时,它们的和有最小值,即若a,b∈R+,且ab=P,P为定值,则a+b 等号当且仅当a=b时成立 .应用 某厂生产化工产品,当年产量在150吨至250吨之间时,某年生产总成本y(万元)与年产量x(吨)之间的关系可近似地表示为 求年产量为多少吨时,每吨的平均成本最低?解:每吨平均成本为(万元),则≥10即当且仅当即x=200时,取等号小结: 用均值不等式解决此类问题时,应按如下步骤进行: 1、先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数; 2、建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题; 3、在定义域内,求出函数的最大值或最小值;4、正确写出答案.求最值已知:0<x<,求函数y=x(1-3x)的最大值.利用二次函数求某一区间的最值分析一、原函数式可化为:y=-3x2+x,分析二、挖掘隐含条件∵3x+1-3x=1为定值,且0<x<则1-3x>0;即x=ymax=∵0<x<,∴1-3x>0∴y=x(1-3x)=3x(1-3x)当且仅当 3x=1-3x 可用均值不等式法解:小结: 1、利用上述重要不等式求函数的最值时务必注意三点达到:一正二定三能等!具体指的是什么?(1)各项必须为正;(2)含变数的各项和或积必须为定值;(3)必须有自变量值能使函数取到 = 号.证明 2、主要用到的方法和技巧是:凑、拆,使之出现和为定值或积为定值特征. 求证:在所有周长相同的矩形中,正方形的面积最大;在所有面积相同的矩形中,正方形的周长最短.设矩形的长为x,宽为y,那么该矩形的周长2(x+y),面积为xy,这样问题就转化为: (1)如果2(x+y)(从而x+y)为定值,那么正数x、y 相等时,xy最大. (2)如果 xy为定值,那么正数 x=y时,2(x+y)最小,(从而 x+y)最小. 解:课堂小结(当且仅当a=b时,等号成立). 1、经过本节课的学习,我们得到了一个基本不等式其中,a>0,b>0 2、两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M为定值,则ab等号当且仅当a=b时成立. 3、两个正数的积为定值时,它们的和有最小值,即若a,b∈R+,且ab=P,P为定值,则a+b 等号当且仅当a=b时成立 . 4、利用上述重要不等式求函数的最值时务必注意三点达到:一正二定三能等! (2005 上海)已知a、b、c都是正数,求证(a+b)(b+c)(c+a)≥8abc.解:∵a,b,c都是正数∴a+b≥2 b+c≥2 c+a≥2 ∴(a+b)(b+c)(c+a) 即(a+b)(b+c)(c+a)≥8abc.高考链接课堂练习 1、若x>0,f(x)= 的最小值为_______;此时x=_______.若x>0,f(x)= 的最小值为_______;此时x=_______.122-12-2直接应用基本不等式即可,注意等号成立的条件!2、阅读下题的各种解法,指出有错误的地方. 答:前两种解法中都没有注意等号成立的条件,均值不等式只在等号同时成立的时候,等号才成立.只有第三种解法是对的.还有其他方法吗?3、下列函数中,最小值是4的是( ) 4、建造一个容积为18m3, 深为2m的长方形无盖水池,如果池底和池壁每m2 的造价为200元和150元,那么池的最低造价为 __元.3600C5、求证证明:当且仅当a=5时,等号成立.6、(1)设 a与b都为实数且a+b=3,的最小值___. (2)求函数f(x)=x (4-x) (0-1,则函数的最小值___.49习题答案1.(1) 设两个正数为a,b,则a>0,b>0,且ab=36,所以 a+b
当且仅当a=b=6时取等号.
答:当这两个正数均为6时,它们的和最小.设两个正数为,,依题意a>0,b>0,且a+b=18,所以
当且仅当a=b=9时,取等号.
答:当这两个正数均为9时,它们的和最小.
当且仅当a=b=6时取等号.
答:当这两个正数均为6时,它们的和最小.设两个正数为,,依题意a>0,b>0,且a+b=18,所以
当且仅当a=b=9时,取等号.
答:当这两个正数均为9时,它们的和最小.
