中考数学专题复习(二十) 分类讨论专题(考点+例题精讲+习题+答案)
文档属性
| 名称 | 中考数学专题复习(二十) 分类讨论专题(考点+例题精讲+习题+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 275.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 13:31:03 | ||
图片预览




文档简介
分类讨论专题
一.分类讨论思想
当数学问题不宜统一方法处理时,我们常常根据研究对象性质的差异,按照一定的分类方法或标准,将问题分为全而不重,广而不漏的若干类,然后逐类分别讨论,再把结论汇总,得出问题的答案的思想。这就是主要考查了分类讨论的数学思想方法。
一:【要点梳理】
1.数学问题比较复杂时,有时可以将其分割成若干个小问题或一系列步骤,从而通过问题的局部突破来实现整体解决,正确应用分类思想,是完整接替的基础。而在学业考试中,分类讨论思想也贯穿其中,命题者经常利用分类讨论题来加大试卷的区分度,很多压轴题也都设计分类讨论。由此可见分类思想的重要性,在数学中,我们常常需要根据研究队形性质的差异,分个中不同情况予以观察,这种分类思考的方法是一种重要的数学思想方法的解题策略,掌握分类的方法,领会其实质,对于加深基础知识的理解,提高分级问题、解决问题的能力都是十分重要的。
2.分类讨论设计全部初中数学的知识点,其关键是要弄清楚引起分类的原因,明确分类讨论的对象和标准,应该按可能出现的情况做出既不重复,又不遗漏,分门别类加以讨论求解,再将不同结论综合归纳,得出正确答案。
3.热点内容
(1).实数的分类。
(2).绝对值、算术根
(3).各类函数的自变量取值范围
(4).函数的增减性:
(5).点与直线的位置关系、直线与圆的位置关系、圆与直线的位置关系。
(6).三角形的分类、四边形的分类
二:【例题与练习】
例1、.如图,反比例函数的图象与直线的交点为A,B,过点A作轴的平行线与过点B作轴的平行线相交于点C,则△ABC的面积为?
【答案】8。
【考点】反比例函数系数的几何意义。
【分析】双曲线上任意一点引轴、轴垂线,所得矩形面积为||,根据反比例函数的中心对称特点可知△ABC的是面积2||=2×4=8。故选A。
例2、已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是多少?
答案:
例3、某果品基地用汽车装运A、B、C三种不同品牌的水果到外地销售,按规定每辆汽车只能装同种水果,且必须装满,其中A、B、C三种水果的重量及利润按下表提供信息:
水果品牌 A B C
每辆汽车载重量(吨) 2.2 2.1 2
每吨水果可获利润(百元) 6 8 5
(1)若用7辆汽车装运A、C两种水果共15吨到甲地销售,如何安排汽车装运A、C两种水果?
(2)计划用20辆汽车装运A、B、C三种不同水果共42吨到乙地销售(每种水果不少于2车),请你设计一种装运方案,可使果品基地获得最大利润,并求出最大利润.
答案:
解:(1)设安排x辆汽车装运A种水果,则安排(7-x)辆汽车装运C种水果.
根据题意得,2.2x +2(7-x)=15
解得,x=5,∴7-x=2
答:安排5辆汽车装运A种水果,安排2辆汽车装运C种水果。
(2)设安排m辆汽车装运A种水果,安排n辆汽车装运B种水果,则安排(20-m-n)辆装运C种水果。根据题意得,2.2m+2.1n+2(20-m-n)= 42
∴n =20-2m
又∵ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )∴ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ∴ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) (m是整数)
设此次装运所获的利润为w,则w=6×2.2 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )m +8×2.1n +5×2×(20-m-n)=-10.4m+336…
∵-10.4<0, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ∴W随m的增大而减小,
∴当m=2时,W=315.2(百元)=31520(元)
即,各用2辆车装运A、C种水果,用16辆车装运B种水果使果品基地获得最大利润,最大利润为31520元.
例4、填空
①如图,⊙O的半径为2,弦AB垂直平分半径OC与D,则弦AB的长为 。
答案:
②在实数范围内因式分解_____________________。
答案:
③某班第二组女生参加体育测试,仰卧起坐的成绩(单位:个)如下:
43、41、39、40、37.这组数据的中位数是___________;标准差是_______________。
答案:40 2
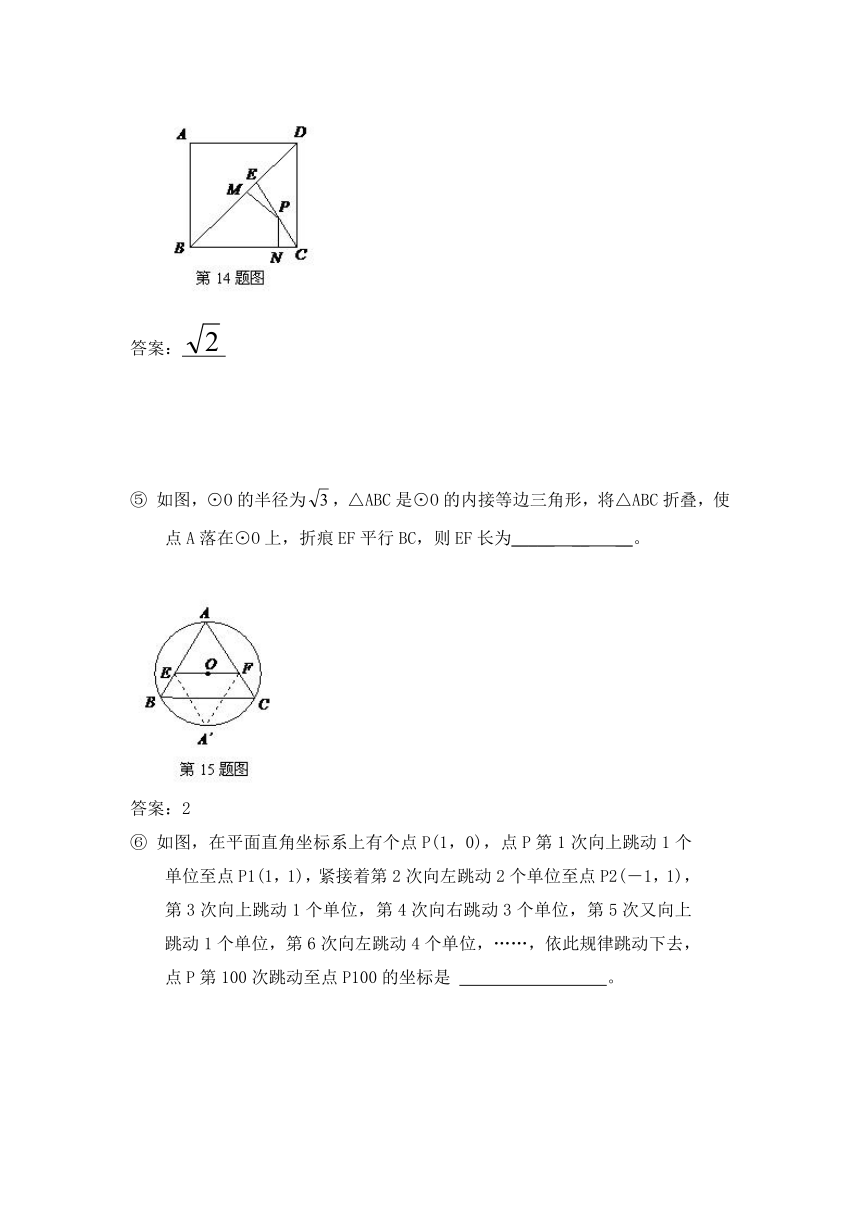
④ 如图,边长为2的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN= ;
答案:
⑤ 如图,⊙O的半径为,△ABC是⊙O的内接等边三角形,将△ABC折叠,使点A落在⊙O上,折痕EF平行BC,则EF长为_____ __ __。
答案:2
⑥ 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。
答案:(26 ,50)
例5、选择。
①下列运算正确的是 ( )
A. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) B. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) C. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) D. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案:D
②已知半径分别为5 cm和8 cm的两圆相交,则它们的圆心距可能是( )
A.1 cm B.3 cm C.10 cm D.15 cm
答案:C
③已知⊙O1的半径为5cm,⊙O2的半径为3cm,圆心距O1O2=2,那么⊙O1与⊙O2的位置关系是( )
A.相离 B.外切 C.相交 D.内切
答案:D
例6.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A、2 B、3 C、4 D、5
考点:三角形的面积 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ).
专题:网格型 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ).
分析:根据三角形ABC的面积为2,可知三角形的底边长为4,高为1,或者底边为2,高为2,可通过在正方形网格中画图得出结果.
解答:解:C点所有的情况如图所示:
故选C.
点评:本题考查了三角形的面积的求法,此类题应选取分类的标准,才能做到不遗不漏,难度适中.
例7.某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色
乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸
奖一次,得奖的概率是 ▲ .
【答案】。
【考点】概率。
【分析】列举出所有情况,看所求的情况占总情况的多少即可:
∵一次摸出两个球的所有等可能情况有(红1,红2),(红1,白1),(红1,白2),(红2,白1),
(红2,白2),(白1,白2)6种,其中两球颜色相同的有2种,
∴顾客摸奖得奖的概率是。
例8.在一次数学探究性学习活动中, 某学习小组要制作一个圆锥体模型, 操作规则是: 在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面。他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二。(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切。方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由。
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由。
答案:解:(1)理由如下:
∵扇形的弧长=16×π/2=8π,圆锥底面周长=2πr
∴圆的半径是4 cm
由于所给正方形对角线的长为16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,而制作这样的圆锥实际需要正方形纸片的对角线长为16+4+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )=20+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),20+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )>16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
∴方案1不可行
(2)方案2可行
求解过程如下:
设圆锥的底面半径为r cm,圆锥的母线长为Rcm,则
(1+ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ))r+R=16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2πr= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
由①②可得R= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,r= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm
故所求圆锥的母线长为 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,底面圆的半径为 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm
例9.已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点.
(1)如图1,若∠AOB=60°,求抛物线C的解析式;
(2)如图2,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线C′,求抛物线C、C′的解析式;
(3)在(2)的条件下,设A′为抛物线C′的顶点,求抛物线C或C′上使得PB=PA'的点P的坐标.
考点:二次函数综合题;点的坐标;待定系数法求二次函数解析式;旋转的性质;相似三角形的判定与性质.分析:(1)先连接AB,根据A点是抛物线C的顶点,且C交x轴于O、B,得出AO=AB,再根据∠AOB=60°,得出△ABO是等边三角形,再过A作AE⊥x轴于E,在Rt△OAE中,求出OE、AE的值,即可求出顶点A的坐标,最后设抛物线C的解析式,求出a的值,从而得出抛物线C的解析式;
(2)先过A作AE⊥OB于E,根据题意得出OE=OB=2,再根据直线OA的解析式为y=x,得出AE=OE=2,求出点A的坐标,再将A、B、O的坐标代入y=ax2+bx+c(a<0)中,求出a的值,得出抛物线C的解析式,再根据抛物线C、C′关于原点对称,从而得出抛物线C′的解析式;
(3)先作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由(2)知,抛物线C′的顶点为A′(-2,-2),得出A′B的中点M的坐标,再作MH⊥x轴于H,得出△MHN∽△BHM,则MH2=HN HB,求出N点的坐标,再根据直线l过点M(1,-1)、N(,0),得出直线l的解析式,求出x的值,再根据抛物线C上存在两点使得PB=PA',从而得出P1,P2坐标,再根据抛物线C′上也存在两点使得PB=PA',得出P3,P4的坐标,即可求出答案.解答:解:(1)连接AB.
∵A点是抛物线C的顶点,且C交x轴于O、B,
∴AO=AB,
又∵∠AOB=60°,
∴△ABO是等边三角形,
过A作AE⊥x轴于E,在Rt△OAE中,
∴OE=2,AE=2,
∴顶点A的坐标为(2,2)
设抛物线C的解析式为y=a(x-2)2+2(a≠0),
将O(0,0)的坐标代入,
求得:a=-,
∴抛物线C的解析式为y=-x2+2x.
(2)过A作AE⊥OB于E,
∵抛物线C:y=ax2+bx+c(a<0)过原点和B(4,0),顶点为A,
∴OE=OB=2,
又∵直线OA的解析式为y=x,
∴AE=OE=2,
∴点A的坐标为(2,2),
将A、B、O的坐标代入y=ax2+bx+c(a<0)中,
∴a=-,
∴抛物线C的解析式为y=-x2+2x,
又∵抛物线C、C′关于原点对称,
∴抛物线C′的解析式为y=x2+2x;
(3)作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),
由前可知,抛物线C′的顶点为A′(-2,-2),
故A′B的中点M的坐标为(1,-1).
作MH⊥x轴于H,
∴△MHN∽△BHM,则MH2=HN HB,即12=(1-n)(4-1),
∴n=,即N点的坐标为(,0).
∵直线l过点M(1,-1)、N(,0),
∴直线l的解析式为y=-3x+2,
解得,x=5±.
∴在抛物线C上存在两点使得PB=PA',其坐标分别为
P1(5+,-13-3),P2(5-,-13+3);
解得,x=-5±.
∴在抛物线C′上也存在两点使得PB=PA',其坐标分别为
P3(-5+,17-3),P4(-5-,17+3).
∴点P的坐标是:P1(5+,-13-3),P2(5-,-13+3),P3(-5+,17-3),P4(-5-,17+3).点评:本题是二次函数的综合,其中涉及到的知识点有旋转的性质,点的坐标,待定系数法求二次函数等知识点,难度较大,综合性较强.
“分类讨论”练习
1.已知AB是圆的直径,AC是弦,AB=2,AC=,弦AD=1,则∠CAD= .
2. 若(x2-x-1)=1,则x=___________.
3. 已知等腰三角形一腰上的中线将它的周长分为9和12两部分,则腰长为,底边长为_______.
4.若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为( )
A. B. C. 或 D. a+b或a-b
5.同一平面上的四个点,过每两点画一直线,则直线的条数是( )
A. 1 B. 4 C. 6 D. 1或4或6
6. 若
A.5或-1 B.-5或1 C.5或1 D.-5或-1
7.已知抛物线y=ax2+bx+c经过点(1,2).
(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且△ABC为等边三角形,求b的值.
(2)若abc=4,且a≥b≥c,求|a|+|b|+|c|的最小值.
8.长宽都为整数的矩形,可以分成边长都为整数的小正方形。
例如一个边长24的矩形:
可以分成三种情况:
(1)
(2)
(3)
一个长宽为36的矩形,可以怎样分成小正方形,请画出你的不同分法。
9.已知与是反比例函数图象上的两个点.
(1)求的值;
(2)若点,则在反比例函数图象上是否存在点,使得以四点为顶点的四边形为梯形?若存在,求出点的坐标;若不存在,请说明理由.
10.如图,在直角坐标系中,矩形的顶点与坐标原点重合,顶点在坐标轴上,,.动点从点出发,以的速度沿轴匀速向点运动,到达点即停止.设点运动的时间为.
(1)过点作对角线的垂线,垂足为点.求的长与时间的函数关系式,并写出自变量的取值范围;
(2)在点运动过程中,当点关于直线的对称点恰好落在对角线上时,求此时直线的函数解析式;
(3)探索:以三点为顶点的的面积能否达到矩形面积的?请说明理由.
练习答案
1. 15°或105°
2. 2、-1、0、-2
3. 腰长6底边9或腰长8底边5
4.C 5.D 6.C
7. 解:⑴由题意,a+b+c=2, ∵a=1,∴b+c=1
抛物线顶点为A(-,c-)
设B(x1,0),C(x2,0),∵x1+x2=-b,x1x2=c,△=b2-4c>0
∴|BC|=| x1-x2|===
∵△ABC为等边三角形,∴ -c=
即b2-4c=2·,∵b2-4c>0,∴=2
∵c=1-b, ∴b2+4b-16=0, b=-2±2
所求b值为-2±2
⑵∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾.
∴a>0.
∵b+c=2-a,bc=
∴b、c是一元二次方程x2-(2-a)x+=0的两实根.
∴△=(2-a)2-4×≥0,
∴a3-4a2+4a-16≥0, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) 即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,∴a、b、c为全大于0或一正二负.
①若a、b、c均大于0,∵a≥4,与a+b+c=2矛盾;
②若a、b、c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵ a≥4, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.
8.分7种情况画图
9.解:(1)由,得,因此
(2)如图1,作轴,为垂足,则,,,因此.
由于点与点的横坐标相同,因此轴,从而.
当为底时,由于过点且平行于的直线与双曲线只有一个公共点,
故不符题意.
当为底时,过点作的平行线,交双曲线于点,
过点分别作轴,轴的平行线,交于点.
由于,设,则,,
由点,得点.
因此,
解之得(舍去),因此点.
此时,与的长度不等,故四边形是梯形.
如图2,当为底时,过点作的平行线,与双曲线在第一象限内的交点为.
由于,因此,从而.作轴,为垂足,
则,设,则,
由点,得点,
因此.
解之得(舍去),因此点.
此时,与的长度不相等,故四边形是梯形.
如图3,当过点作的平行线,与双曲线在第三象限内的交点为时,
同理可得,点,四边形是梯形.
综上所述,函数图象上存在点,使得以四点为顶点的四边形为梯形,点的坐标为:或或.
10.解:(1)在矩形中,,,
,.
,即,
当点运动到点时即停止运动,此时的最大值为.
所以,的取值范围是.
(2)当点关于直线的对称点恰好在对角线上时,三点应在一条直线上(如答图2).
,.
,
.
.点的坐标为
设直线的函数解析式为.将点和点代入解析式,得解这个方程组,得
此时直线的函数解析式是.
(3)由(2)知,当时,三点在一条直线上,此时点 不构成三角形.
故分两种情况:
(i)当时,点位于的内部(如答图3).
过点作,垂足为点,由
可得.
.
若,则应有,即.
此时,,所以该方程无实数根.
所以,当时,以为顶点的的面积不能达到矩形面积的.
(ii)当时,点位于的外部.(如答图4)
此时.
若,则应有,即.
解这个方程,得,(舍去).
由于,.
而此时,所以也不符合题意,故舍去.
所以,当时,以为顶点的的面积也不能达到矩形面积的.
综上所述,以为顶点的的面积不能达到矩形面积的.
分成两个正方形,面积分别为4,4
分成8个正方形,面积每个都是1
分成5个正方形,1个面积为4,4个面积是1
y
x
B
C
P
O
A
T
图2
图1
图3
y
x
B
C
P
O
A
T
(答图1)
y
x
B
C
P
O
A
T
(答图2)
2
1
y
x
B
C
P
O
A
T
(答图3)
E
一.分类讨论思想
当数学问题不宜统一方法处理时,我们常常根据研究对象性质的差异,按照一定的分类方法或标准,将问题分为全而不重,广而不漏的若干类,然后逐类分别讨论,再把结论汇总,得出问题的答案的思想。这就是主要考查了分类讨论的数学思想方法。
一:【要点梳理】
1.数学问题比较复杂时,有时可以将其分割成若干个小问题或一系列步骤,从而通过问题的局部突破来实现整体解决,正确应用分类思想,是完整接替的基础。而在学业考试中,分类讨论思想也贯穿其中,命题者经常利用分类讨论题来加大试卷的区分度,很多压轴题也都设计分类讨论。由此可见分类思想的重要性,在数学中,我们常常需要根据研究队形性质的差异,分个中不同情况予以观察,这种分类思考的方法是一种重要的数学思想方法的解题策略,掌握分类的方法,领会其实质,对于加深基础知识的理解,提高分级问题、解决问题的能力都是十分重要的。
2.分类讨论设计全部初中数学的知识点,其关键是要弄清楚引起分类的原因,明确分类讨论的对象和标准,应该按可能出现的情况做出既不重复,又不遗漏,分门别类加以讨论求解,再将不同结论综合归纳,得出正确答案。
3.热点内容
(1).实数的分类。
(2).绝对值、算术根
(3).各类函数的自变量取值范围
(4).函数的增减性:
(5).点与直线的位置关系、直线与圆的位置关系、圆与直线的位置关系。
(6).三角形的分类、四边形的分类
二:【例题与练习】
例1、.如图,反比例函数的图象与直线的交点为A,B,过点A作轴的平行线与过点B作轴的平行线相交于点C,则△ABC的面积为?
【答案】8。
【考点】反比例函数系数的几何意义。
【分析】双曲线上任意一点引轴、轴垂线,所得矩形面积为||,根据反比例函数的中心对称特点可知△ABC的是面积2||=2×4=8。故选A。
例2、已知关于的一元二次方程有两个不相等的实数根,则实数的取值范围是多少?
答案:
例3、某果品基地用汽车装运A、B、C三种不同品牌的水果到外地销售,按规定每辆汽车只能装同种水果,且必须装满,其中A、B、C三种水果的重量及利润按下表提供信息:
水果品牌 A B C
每辆汽车载重量(吨) 2.2 2.1 2
每吨水果可获利润(百元) 6 8 5
(1)若用7辆汽车装运A、C两种水果共15吨到甲地销售,如何安排汽车装运A、C两种水果?
(2)计划用20辆汽车装运A、B、C三种不同水果共42吨到乙地销售(每种水果不少于2车),请你设计一种装运方案,可使果品基地获得最大利润,并求出最大利润.
答案:
解:(1)设安排x辆汽车装运A种水果,则安排(7-x)辆汽车装运C种水果.
根据题意得,2.2x +2(7-x)=15
解得,x=5,∴7-x=2
答:安排5辆汽车装运A种水果,安排2辆汽车装运C种水果。
(2)设安排m辆汽车装运A种水果,安排n辆汽车装运B种水果,则安排(20-m-n)辆装运C种水果。根据题意得,2.2m+2.1n+2(20-m-n)= 42
∴n =20-2m
又∵ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )∴ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ∴ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) (m是整数)
设此次装运所获的利润为w,则w=6×2.2 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )m +8×2.1n +5×2×(20-m-n)=-10.4m+336…
∵-10.4<0, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ∴W随m的增大而减小,
∴当m=2时,W=315.2(百元)=31520(元)
即,各用2辆车装运A、C种水果,用16辆车装运B种水果使果品基地获得最大利润,最大利润为31520元.
例4、填空
①如图,⊙O的半径为2,弦AB垂直平分半径OC与D,则弦AB的长为 。
答案:
②在实数范围内因式分解_____________________。
答案:
③某班第二组女生参加体育测试,仰卧起坐的成绩(单位:个)如下:
43、41、39、40、37.这组数据的中位数是___________;标准差是_______________。
答案:40 2
④ 如图,边长为2的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN= ;
答案:
⑤ 如图,⊙O的半径为,△ABC是⊙O的内接等边三角形,将△ABC折叠,使点A落在⊙O上,折痕EF平行BC,则EF长为_____ __ __。
答案:2
⑥ 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。
答案:(26 ,50)
例5、选择。
①下列运算正确的是 ( )
A. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) B. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) C. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) D. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案:D
②已知半径分别为5 cm和8 cm的两圆相交,则它们的圆心距可能是( )
A.1 cm B.3 cm C.10 cm D.15 cm
答案:C
③已知⊙O1的半径为5cm,⊙O2的半径为3cm,圆心距O1O2=2,那么⊙O1与⊙O2的位置关系是( )
A.相离 B.外切 C.相交 D.内切
答案:D
例6.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A、2 B、3 C、4 D、5
考点:三角形的面积 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ).
专题:网格型 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ).
分析:根据三角形ABC的面积为2,可知三角形的底边长为4,高为1,或者底边为2,高为2,可通过在正方形网格中画图得出结果.
解答:解:C点所有的情况如图所示:
故选C.
点评:本题考查了三角形的面积的求法,此类题应选取分类的标准,才能做到不遗不漏,难度适中.
例7.某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色
乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸
奖一次,得奖的概率是 ▲ .
【答案】。
【考点】概率。
【分析】列举出所有情况,看所求的情况占总情况的多少即可:
∵一次摸出两个球的所有等可能情况有(红1,红2),(红1,白1),(红1,白2),(红2,白1),
(红2,白2),(白1,白2)6种,其中两球颜色相同的有2种,
∴顾客摸奖得奖的概率是。
例8.在一次数学探究性学习活动中, 某学习小组要制作一个圆锥体模型, 操作规则是: 在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面。他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二。(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切。方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由。
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由。
答案:解:(1)理由如下:
∵扇形的弧长=16×π/2=8π,圆锥底面周长=2πr
∴圆的半径是4 cm
由于所给正方形对角线的长为16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,而制作这样的圆锥实际需要正方形纸片的对角线长为16+4+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )=20+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),20+4 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )>16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
∴方案1不可行
(2)方案2可行
求解过程如下:
设圆锥的底面半径为r cm,圆锥的母线长为Rcm,则
(1+ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ))r+R=16 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2πr= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
由①②可得R= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,r= ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm
故所求圆锥的母线长为 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm,底面圆的半径为 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )cm
例9.已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点.
(1)如图1,若∠AOB=60°,求抛物线C的解析式;
(2)如图2,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线C′,求抛物线C、C′的解析式;
(3)在(2)的条件下,设A′为抛物线C′的顶点,求抛物线C或C′上使得PB=PA'的点P的坐标.
考点:二次函数综合题;点的坐标;待定系数法求二次函数解析式;旋转的性质;相似三角形的判定与性质.分析:(1)先连接AB,根据A点是抛物线C的顶点,且C交x轴于O、B,得出AO=AB,再根据∠AOB=60°,得出△ABO是等边三角形,再过A作AE⊥x轴于E,在Rt△OAE中,求出OE、AE的值,即可求出顶点A的坐标,最后设抛物线C的解析式,求出a的值,从而得出抛物线C的解析式;
(2)先过A作AE⊥OB于E,根据题意得出OE=OB=2,再根据直线OA的解析式为y=x,得出AE=OE=2,求出点A的坐标,再将A、B、O的坐标代入y=ax2+bx+c(a<0)中,求出a的值,得出抛物线C的解析式,再根据抛物线C、C′关于原点对称,从而得出抛物线C′的解析式;
(3)先作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由(2)知,抛物线C′的顶点为A′(-2,-2),得出A′B的中点M的坐标,再作MH⊥x轴于H,得出△MHN∽△BHM,则MH2=HN HB,求出N点的坐标,再根据直线l过点M(1,-1)、N(,0),得出直线l的解析式,求出x的值,再根据抛物线C上存在两点使得PB=PA',从而得出P1,P2坐标,再根据抛物线C′上也存在两点使得PB=PA',得出P3,P4的坐标,即可求出答案.解答:解:(1)连接AB.
∵A点是抛物线C的顶点,且C交x轴于O、B,
∴AO=AB,
又∵∠AOB=60°,
∴△ABO是等边三角形,
过A作AE⊥x轴于E,在Rt△OAE中,
∴OE=2,AE=2,
∴顶点A的坐标为(2,2)
设抛物线C的解析式为y=a(x-2)2+2(a≠0),
将O(0,0)的坐标代入,
求得:a=-,
∴抛物线C的解析式为y=-x2+2x.
(2)过A作AE⊥OB于E,
∵抛物线C:y=ax2+bx+c(a<0)过原点和B(4,0),顶点为A,
∴OE=OB=2,
又∵直线OA的解析式为y=x,
∴AE=OE=2,
∴点A的坐标为(2,2),
将A、B、O的坐标代入y=ax2+bx+c(a<0)中,
∴a=-,
∴抛物线C的解析式为y=-x2+2x,
又∵抛物线C、C′关于原点对称,
∴抛物线C′的解析式为y=x2+2x;
(3)作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),
由前可知,抛物线C′的顶点为A′(-2,-2),
故A′B的中点M的坐标为(1,-1).
作MH⊥x轴于H,
∴△MHN∽△BHM,则MH2=HN HB,即12=(1-n)(4-1),
∴n=,即N点的坐标为(,0).
∵直线l过点M(1,-1)、N(,0),
∴直线l的解析式为y=-3x+2,
解得,x=5±.
∴在抛物线C上存在两点使得PB=PA',其坐标分别为
P1(5+,-13-3),P2(5-,-13+3);
解得,x=-5±.
∴在抛物线C′上也存在两点使得PB=PA',其坐标分别为
P3(-5+,17-3),P4(-5-,17+3).
∴点P的坐标是:P1(5+,-13-3),P2(5-,-13+3),P3(-5+,17-3),P4(-5-,17+3).点评:本题是二次函数的综合,其中涉及到的知识点有旋转的性质,点的坐标,待定系数法求二次函数等知识点,难度较大,综合性较强.
“分类讨论”练习
1.已知AB是圆的直径,AC是弦,AB=2,AC=,弦AD=1,则∠CAD= .
2. 若(x2-x-1)=1,则x=___________.
3. 已知等腰三角形一腰上的中线将它的周长分为9和12两部分,则腰长为,底边长为_______.
4.若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为( )
A. B. C. 或 D. a+b或a-b
5.同一平面上的四个点,过每两点画一直线,则直线的条数是( )
A. 1 B. 4 C. 6 D. 1或4或6
6. 若
A.5或-1 B.-5或1 C.5或1 D.-5或-1
7.已知抛物线y=ax2+bx+c经过点(1,2).
(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且△ABC为等边三角形,求b的值.
(2)若abc=4,且a≥b≥c,求|a|+|b|+|c|的最小值.
8.长宽都为整数的矩形,可以分成边长都为整数的小正方形。
例如一个边长24的矩形:
可以分成三种情况:
(1)
(2)
(3)
一个长宽为36的矩形,可以怎样分成小正方形,请画出你的不同分法。
9.已知与是反比例函数图象上的两个点.
(1)求的值;
(2)若点,则在反比例函数图象上是否存在点,使得以四点为顶点的四边形为梯形?若存在,求出点的坐标;若不存在,请说明理由.
10.如图,在直角坐标系中,矩形的顶点与坐标原点重合,顶点在坐标轴上,,.动点从点出发,以的速度沿轴匀速向点运动,到达点即停止.设点运动的时间为.
(1)过点作对角线的垂线,垂足为点.求的长与时间的函数关系式,并写出自变量的取值范围;
(2)在点运动过程中,当点关于直线的对称点恰好落在对角线上时,求此时直线的函数解析式;
(3)探索:以三点为顶点的的面积能否达到矩形面积的?请说明理由.
练习答案
1. 15°或105°
2. 2、-1、0、-2
3. 腰长6底边9或腰长8底边5
4.C 5.D 6.C
7. 解:⑴由题意,a+b+c=2, ∵a=1,∴b+c=1
抛物线顶点为A(-,c-)
设B(x1,0),C(x2,0),∵x1+x2=-b,x1x2=c,△=b2-4c>0
∴|BC|=| x1-x2|===
∵△ABC为等边三角形,∴ -c=
即b2-4c=2·,∵b2-4c>0,∴=2
∵c=1-b, ∴b2+4b-16=0, b=-2±2
所求b值为-2±2
⑵∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾.
∴a>0.
∵b+c=2-a,bc=
∴b、c是一元二次方程x2-(2-a)x+=0的两实根.
∴△=(2-a)2-4×≥0,
∴a3-4a2+4a-16≥0, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) 即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,∴a、b、c为全大于0或一正二负.
①若a、b、c均大于0,∵a≥4,与a+b+c=2矛盾;
②若a、b、c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵ a≥4, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.
8.分7种情况画图
9.解:(1)由,得,因此
(2)如图1,作轴,为垂足,则,,,因此.
由于点与点的横坐标相同,因此轴,从而.
当为底时,由于过点且平行于的直线与双曲线只有一个公共点,
故不符题意.
当为底时,过点作的平行线,交双曲线于点,
过点分别作轴,轴的平行线,交于点.
由于,设,则,,
由点,得点.
因此,
解之得(舍去),因此点.
此时,与的长度不等,故四边形是梯形.
如图2,当为底时,过点作的平行线,与双曲线在第一象限内的交点为.
由于,因此,从而.作轴,为垂足,
则,设,则,
由点,得点,
因此.
解之得(舍去),因此点.
此时,与的长度不相等,故四边形是梯形.
如图3,当过点作的平行线,与双曲线在第三象限内的交点为时,
同理可得,点,四边形是梯形.
综上所述,函数图象上存在点,使得以四点为顶点的四边形为梯形,点的坐标为:或或.
10.解:(1)在矩形中,,,
,.
,即,
当点运动到点时即停止运动,此时的最大值为.
所以,的取值范围是.
(2)当点关于直线的对称点恰好在对角线上时,三点应在一条直线上(如答图2).
,.
,
.
.点的坐标为
设直线的函数解析式为.将点和点代入解析式,得解这个方程组,得
此时直线的函数解析式是.
(3)由(2)知,当时,三点在一条直线上,此时点 不构成三角形.
故分两种情况:
(i)当时,点位于的内部(如答图3).
过点作,垂足为点,由
可得.
.
若,则应有,即.
此时,,所以该方程无实数根.
所以,当时,以为顶点的的面积不能达到矩形面积的.
(ii)当时,点位于的外部.(如答图4)
此时.
若,则应有,即.
解这个方程,得,(舍去).
由于,.
而此时,所以也不符合题意,故舍去.
所以,当时,以为顶点的的面积也不能达到矩形面积的.
综上所述,以为顶点的的面积不能达到矩形面积的.
分成两个正方形,面积分别为4,4
分成8个正方形,面积每个都是1
分成5个正方形,1个面积为4,4个面积是1
y
x
B
C
P
O
A
T
图2
图1
图3
y
x
B
C
P
O
A
T
(答图1)
y
x
B
C
P
O
A
T
(答图2)
2
1
y
x
B
C
P
O
A
T
(答图3)
E
同课章节目录
