中考数学专题复习(二十二) 与动态有关的综合题专题(考点+例题精讲+习题+答案)
文档属性
| 名称 | 中考数学专题复习(二十二) 与动态有关的综合题专题(考点+例题精讲+习题+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 00:00:00 | ||
图片预览




文档简介
与动态有关的综合题
动态几何问题就其知识结构而言,它常常集几何、代数知识于一体,是数形结合的完善表现,具有较强的综合性、灵活性和多变性。几何方面常常涉及全等形、相似性、勾股定理、特殊的四边形和圆,代数方面涉及的知识主要有方程、函数、不等式、坐标和解直角三角形等。解决这类问题的基本策略是:1、动中觅静:这里的“静”就是问题中的不变量、不变关系,动中觅静就是在运动变化中探索问题中的不变性。2、动静互化:“静”只是“动”瞬间,是运动的一种特殊形式,动静互化就是抓住“静”的瞬间,使一般情形转化为特殊问题,从而找到“动”与“静”的关系。3、以动制动:以动制动就是建立图形中两个变量的函数关系,通过研究运动函数,用联系发展的观点来研究变动元素的关系。总之,解决动态几何问题的关键是要善于运用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住变化中的不变,以不变应万变。具体做法是:第一,全面阅读题目,了解运动的方式和形式,全方位考察运动中的变与变的量及其位置关系;第二,应用分类讨论思想,将在运动过程中导致图形本质发生变化的各种时刻的图形分类画出,变“动”为“静”;第三,在各类“静态图形”中运用相关的知识和方法进行探索,寻找各个相关几何量之间的关系,建立相应的数学模型进行求解。
考点1 点动
命题规律 点运动问题,即探索几何图形上一个或几个动点在运动变化过程中伴随着等量关系,变量关系,图形的特殊状态,图形间的特殊关系等题目。
以点的运动带动图形的变化,常与方程,函数知识联系在一起。
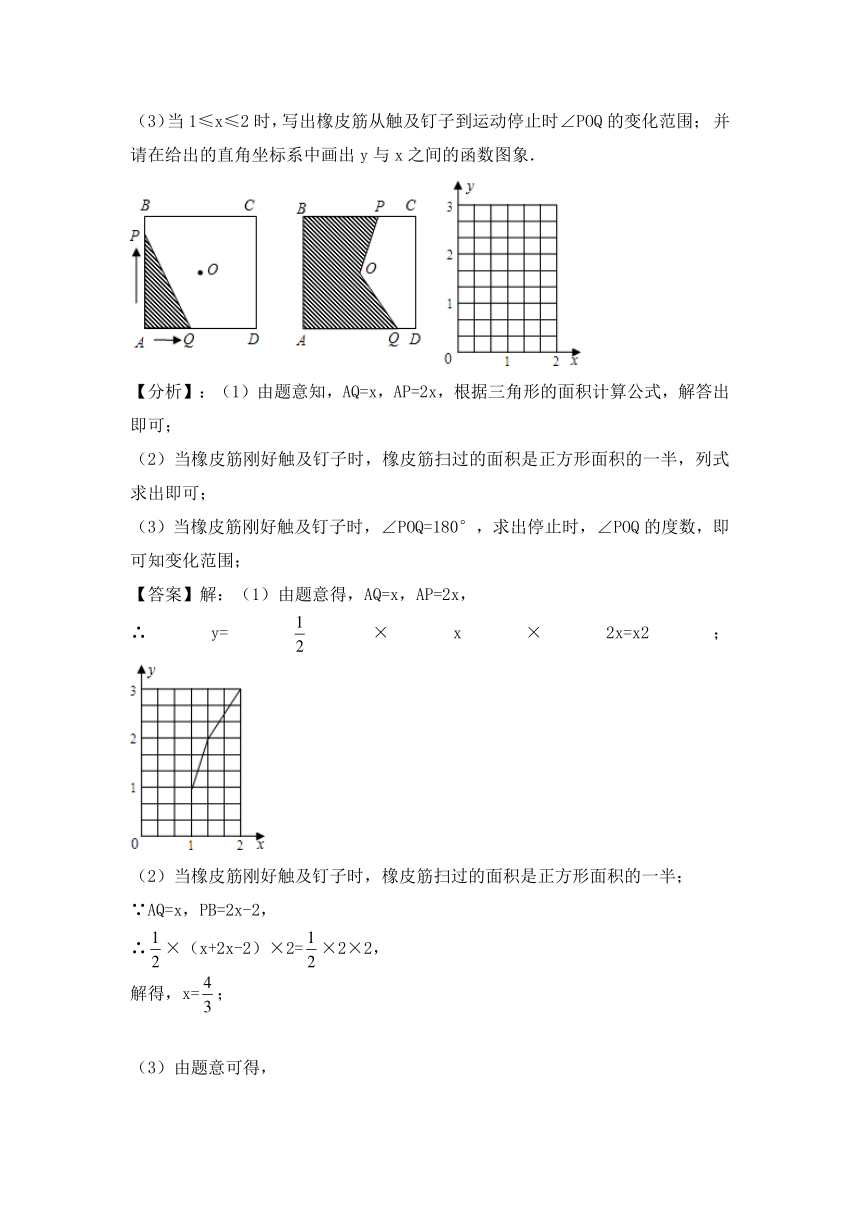
【例1】如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P、Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止;点Q沿A→D方向以每秒1cm的速度运动,到点D停止.P、Q两点用一条可伸缩的细橡皮筋连接,设x秒后橡皮筋扫过的面积为ycm2.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围; 并请在给出的直角坐标系中画出y与x之间的函数图象.
【分析】:(1)由题意知,AQ=x,AP=2x,根据三角形的面积计算公式,解答出即可;
(2)当橡皮筋刚好触及钉子时,橡皮筋扫过的面积是正方形面积的一半,列式求出即可;
(3)当橡皮筋刚好触及钉子时,∠POQ=180°,求出停止时,∠POQ的度数,即可知变化范围;
【答案】解:(1)由题意得,AQ=x,AP=2x,
∴y=×x×2x=x2;
(2)当橡皮筋刚好触及钉子时,橡皮筋扫过的面积是正方形面积的一半;
∵AQ=x,PB=2x-2,
∴×(x+2x-2)×2=×2×2,
解得,x=;
(3)由题意可得,
当橡皮筋刚好触及钉子时,∠POQ=180°,
停止时,OP=,OQ=,PQ=2,
∴OP2+OQ2=PQ2,
∴∠POQ=90°;
∴90°≤∠POQ≤180°;
如图,
①当1≤x≤时,y=3x-2;
②当<x≤2时,y=x.
考点2 线动
命题规律 线动型的问题有两大类即直线(线段)和曲线(包括圆弧)其运动的形式有平移,旋转等。它主要是探索在运动的过程中等量关系,变量关系,图形的特殊状态等,这种题目一般综合性比较强,多半以压轴的形式出现。
【例2】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).
(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;
(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
【答案】:解:(1)由题意,当MN和AB之间的距离为1米时,MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,又因为EM=EN=1米,所以MN=米,所以S△EMN=平方米,即三角通风窗EMN的通风面积为平方米
(2)当MN在矩形区域内滑动,即x∈(0,)时,△EMN的面积S=×MN×(-x)=-x;
当MN在半圆形区域内滑动,即x∈(,)时,△EMN的面积S=(x-)
综上可得S=f(x)= -x+,x∈(0)
(x-) ,x∈();
(3)当MN在矩形区域内滑动时,f(x)在区间(0,)上单调递减,则f(x)<f(0)=;
当MN在半圆形区域内滑动,f(x)=(x-) ≤=等号成立时,x=(+1)
因此当x=(+1)(米)时,每个三角形得到最大通风面积为平方米.
考点3 形动
命题规律 尽管图形的运动更复杂,但它们的运动还有其规律,其主要形式有平移,旋转,翻转对称等,图形在运动过程中的大小和形状是不变的只是位置发生变化,这个类型的考题在逐年增加请留心。
【例3】如图,已知直线y=-x+1交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
(1)求点C、D的坐标
(2)求抛物线的解析式
(3)若抛物线与正方形沿射线AB下滑,直至点C落在x轴上时停止,求抛物线上C、E两点间的抛物线所扫过的面积.
【分析】:(1)分别过C、D两点作x轴、y轴的垂线,利用三角形全等的关系可确定C、D两点的坐标;
(2)根据A、C、D三点的坐标求抛物线解析式;
(3)由平移的性质可判断线段CE所扫过的部分为平行四边形,CC′为底,BC为高,由此求出C、E两点间的抛物线所扫过的面积.
【答案】解:(1)如图,分别过C、D两点作x轴、y轴的垂线,垂足为M、N,
由直线AB的解析式得AO=1,OB=2,
由正方形的性质可证△ADN≌△BAO≌△CBM,
∴DN=BM=AO=1,AN=CM=BO=2,
∴C(3,2),D(1,3);
(2)设抛物线解析式为y=ax2+bx+c,
将A(0,1),C(3,2),D(1,3)三点坐标代入,得
c=1
9a+3b+c=2
a+b+c=3,
解得
a=-
b=
c=1,
∴y=-x2+x+1;
(3)∵AB=BC==,
由△BCC′∽△AOB,得==,
∴CC′=2BC=2,
由割补法可知,抛物线上C、E两点间的抛物线所扫过的面积=S CEE′C′=CC′×BC=2×=10,
即抛物线上C、E两点间的抛物线所扫过的面积为10.
“运动型问题”练习
1.如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
2.如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连结OP,则线段OP的最小长度是 .
3.如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则点P2008的横坐标为 .
4.在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是 ( )
5.挂钟分针的长为10cm,经过45分钟,它的针尖转过的弧长是 ( )
A.cm B.15πcm C.cm D.75πcm
6.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是 ( )
A.3秒或4.8秒 B.3秒 C.4.5秒 D.4.5秒或4.8秒
7.如图,A是半径为12cm的⊙O上的定点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到A地立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时,判断直线BP与⊙O的位置关系,并说明理由.
8.△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合).过M、N分别作AB的垂线交直角边于P、Q两点,线段MN运动的时间为ts.
(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
(3)t为何值时,以C、P、Q为顶点的三角形与△ABC相似?
9.如图,⊙O的半径为1,正方形ABCD顶点B坐标为(5,0),顶点D在⊙O上运动.
(1)当点D运动到与点A、O在同一条直线上时,试证明直线CD与⊙O相切;
(2)当直线CD与⊙O相切时,求CD所在直线对应的函数关系式;
(3)设点D的横坐标为x,正方形ABCD的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值.
10.如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为S,S关于t的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
参考答案:
1.12π 2.3 3.2008 4.C 5.B 6.A
7.(1)当∠POA=90°时,点P运动的时间为3s或9s.
(2)点P运动的时间为2s时,直线BP与⊙O相切.
8.(1)①当点P在AC上时,y= eq \f(,2)t2(0≤t≤1);②当点P在BC上时,y=- eq \f(,6)t2+ eq \f(2,3)t(1<t≤3).
(2)当t=s时,四边形MNQP为矩形.
(3)当t=s或s时,以C、P、Q为顶点的三角形与相似.
9.(1)因为A、D、O三点在同一条直线上,∠ADC=90° ,所以∠CDO=90°,所以CD是⊙O的切线.
(2)①当切点D在第四象限时,OD所在直线的函数关系式为y=-x;②当切点在第二象限时,OD所在直线对应的函数关系式为y=-x.
(3)正方形的面积S与x之间的函数关系式为S=13-5x.又∵D点在圆上运动,∴-1≤x≤1.∴ S的最大值是18,最小值是8.
10.(1)①AB=2;直角梯形OABC的面积为12;
②当2<t<4时,直角梯形OABC被直线l扫过的面积S=-t2+8t-4.
(2)存在点P,使△PDE为等腰直角三角形.满足条件的点P有P1(-12,4),P2(-4,4),P3(-,4),P4(4,4),P5(8,4).
(第1题)
(第2题)
(第3题)
A. B. C. D.
(第6题)
(第7题)
(第8题)
(第9题)
图1
图2
E
Q
(第10题)
动态几何问题就其知识结构而言,它常常集几何、代数知识于一体,是数形结合的完善表现,具有较强的综合性、灵活性和多变性。几何方面常常涉及全等形、相似性、勾股定理、特殊的四边形和圆,代数方面涉及的知识主要有方程、函数、不等式、坐标和解直角三角形等。解决这类问题的基本策略是:1、动中觅静:这里的“静”就是问题中的不变量、不变关系,动中觅静就是在运动变化中探索问题中的不变性。2、动静互化:“静”只是“动”瞬间,是运动的一种特殊形式,动静互化就是抓住“静”的瞬间,使一般情形转化为特殊问题,从而找到“动”与“静”的关系。3、以动制动:以动制动就是建立图形中两个变量的函数关系,通过研究运动函数,用联系发展的观点来研究变动元素的关系。总之,解决动态几何问题的关键是要善于运用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住变化中的不变,以不变应万变。具体做法是:第一,全面阅读题目,了解运动的方式和形式,全方位考察运动中的变与变的量及其位置关系;第二,应用分类讨论思想,将在运动过程中导致图形本质发生变化的各种时刻的图形分类画出,变“动”为“静”;第三,在各类“静态图形”中运用相关的知识和方法进行探索,寻找各个相关几何量之间的关系,建立相应的数学模型进行求解。
考点1 点动
命题规律 点运动问题,即探索几何图形上一个或几个动点在运动变化过程中伴随着等量关系,变量关系,图形的特殊状态,图形间的特殊关系等题目。
以点的运动带动图形的变化,常与方程,函数知识联系在一起。
【例1】如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P、Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止;点Q沿A→D方向以每秒1cm的速度运动,到点D停止.P、Q两点用一条可伸缩的细橡皮筋连接,设x秒后橡皮筋扫过的面积为ycm2.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围; 并请在给出的直角坐标系中画出y与x之间的函数图象.
【分析】:(1)由题意知,AQ=x,AP=2x,根据三角形的面积计算公式,解答出即可;
(2)当橡皮筋刚好触及钉子时,橡皮筋扫过的面积是正方形面积的一半,列式求出即可;
(3)当橡皮筋刚好触及钉子时,∠POQ=180°,求出停止时,∠POQ的度数,即可知变化范围;
【答案】解:(1)由题意得,AQ=x,AP=2x,
∴y=×x×2x=x2;
(2)当橡皮筋刚好触及钉子时,橡皮筋扫过的面积是正方形面积的一半;
∵AQ=x,PB=2x-2,
∴×(x+2x-2)×2=×2×2,
解得,x=;
(3)由题意可得,
当橡皮筋刚好触及钉子时,∠POQ=180°,
停止时,OP=,OQ=,PQ=2,
∴OP2+OQ2=PQ2,
∴∠POQ=90°;
∴90°≤∠POQ≤180°;
如图,
①当1≤x≤时,y=3x-2;
②当<x≤2时,y=x.
考点2 线动
命题规律 线动型的问题有两大类即直线(线段)和曲线(包括圆弧)其运动的形式有平移,旋转等。它主要是探索在运动的过程中等量关系,变量关系,图形的特殊状态等,这种题目一般综合性比较强,多半以压轴的形式出现。
【例2】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).
(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;
(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
【答案】:解:(1)由题意,当MN和AB之间的距离为1米时,MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,又因为EM=EN=1米,所以MN=米,所以S△EMN=平方米,即三角通风窗EMN的通风面积为平方米
(2)当MN在矩形区域内滑动,即x∈(0,)时,△EMN的面积S=×MN×(-x)=-x;
当MN在半圆形区域内滑动,即x∈(,)时,△EMN的面积S=(x-)
综上可得S=f(x)= -x+,x∈(0)
(x-) ,x∈();
(3)当MN在矩形区域内滑动时,f(x)在区间(0,)上单调递减,则f(x)<f(0)=;
当MN在半圆形区域内滑动,f(x)=(x-) ≤=等号成立时,x=(+1)
因此当x=(+1)(米)时,每个三角形得到最大通风面积为平方米.
考点3 形动
命题规律 尽管图形的运动更复杂,但它们的运动还有其规律,其主要形式有平移,旋转,翻转对称等,图形在运动过程中的大小和形状是不变的只是位置发生变化,这个类型的考题在逐年增加请留心。
【例3】如图,已知直线y=-x+1交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
(1)求点C、D的坐标
(2)求抛物线的解析式
(3)若抛物线与正方形沿射线AB下滑,直至点C落在x轴上时停止,求抛物线上C、E两点间的抛物线所扫过的面积.
【分析】:(1)分别过C、D两点作x轴、y轴的垂线,利用三角形全等的关系可确定C、D两点的坐标;
(2)根据A、C、D三点的坐标求抛物线解析式;
(3)由平移的性质可判断线段CE所扫过的部分为平行四边形,CC′为底,BC为高,由此求出C、E两点间的抛物线所扫过的面积.
【答案】解:(1)如图,分别过C、D两点作x轴、y轴的垂线,垂足为M、N,
由直线AB的解析式得AO=1,OB=2,
由正方形的性质可证△ADN≌△BAO≌△CBM,
∴DN=BM=AO=1,AN=CM=BO=2,
∴C(3,2),D(1,3);
(2)设抛物线解析式为y=ax2+bx+c,
将A(0,1),C(3,2),D(1,3)三点坐标代入,得
c=1
9a+3b+c=2
a+b+c=3,
解得
a=-
b=
c=1,
∴y=-x2+x+1;
(3)∵AB=BC==,
由△BCC′∽△AOB,得==,
∴CC′=2BC=2,
由割补法可知,抛物线上C、E两点间的抛物线所扫过的面积=S CEE′C′=CC′×BC=2×=10,
即抛物线上C、E两点间的抛物线所扫过的面积为10.
“运动型问题”练习
1.如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
2.如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连结OP,则线段OP的最小长度是 .
3.如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则点P2008的横坐标为 .
4.在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是 ( )
5.挂钟分针的长为10cm,经过45分钟,它的针尖转过的弧长是 ( )
A.cm B.15πcm C.cm D.75πcm
6.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是 ( )
A.3秒或4.8秒 B.3秒 C.4.5秒 D.4.5秒或4.8秒
7.如图,A是半径为12cm的⊙O上的定点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到A地立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时,判断直线BP与⊙O的位置关系,并说明理由.
8.△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合).过M、N分别作AB的垂线交直角边于P、Q两点,线段MN运动的时间为ts.
(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
(3)t为何值时,以C、P、Q为顶点的三角形与△ABC相似?
9.如图,⊙O的半径为1,正方形ABCD顶点B坐标为(5,0),顶点D在⊙O上运动.
(1)当点D运动到与点A、O在同一条直线上时,试证明直线CD与⊙O相切;
(2)当直线CD与⊙O相切时,求CD所在直线对应的函数关系式;
(3)设点D的横坐标为x,正方形ABCD的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值.
10.如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为S,S关于t的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
参考答案:
1.12π 2.3 3.2008 4.C 5.B 6.A
7.(1)当∠POA=90°时,点P运动的时间为3s或9s.
(2)点P运动的时间为2s时,直线BP与⊙O相切.
8.(1)①当点P在AC上时,y= eq \f(,2)t2(0≤t≤1);②当点P在BC上时,y=- eq \f(,6)t2+ eq \f(2,3)t(1<t≤3).
(2)当t=s时,四边形MNQP为矩形.
(3)当t=s或s时,以C、P、Q为顶点的三角形与相似.
9.(1)因为A、D、O三点在同一条直线上,∠ADC=90° ,所以∠CDO=90°,所以CD是⊙O的切线.
(2)①当切点D在第四象限时,OD所在直线的函数关系式为y=-x;②当切点在第二象限时,OD所在直线对应的函数关系式为y=-x.
(3)正方形的面积S与x之间的函数关系式为S=13-5x.又∵D点在圆上运动,∴-1≤x≤1.∴ S的最大值是18,最小值是8.
10.(1)①AB=2;直角梯形OABC的面积为12;
②当2<t<4时,直角梯形OABC被直线l扫过的面积S=-t2+8t-4.
(2)存在点P,使△PDE为等腰直角三角形.满足条件的点P有P1(-12,4),P2(-4,4),P3(-,4),P4(4,4),P5(8,4).
(第1题)
(第2题)
(第3题)
A. B. C. D.
(第6题)
(第7题)
(第8题)
(第9题)
图1
图2
E
Q
(第10题)
同课章节目录
