人教版数学七年级下册 8.3实际问题与二元一次方程组(1) 课件(共18张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.3实际问题与二元一次方程组(1) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 226.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 07:12:21 | ||
图片预览






文档简介
(共18张PPT)
8.3实际问题与二元一次方程组(1)
教学目标
(1)经历运用方程解决实际问题的过程,体会方程是刻画现实世界的有效数学模型.
教学重点与难点
难点:确定解题策略,比较估算与精确计算.
(2)能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程.
(3)学会比较估算与静确计算以及检验方程组的解是否符号合题意并正确作答.
(4)培养分析,解决问题的能力,体会二元一次方程组的应用价值,感受数学文化.
重点:以方程组为工具分析,解决含有多个未知数的实际问题..
列方程组解应用题的步骤:
审题
设未知数
列方程组
解方程组
检验
答
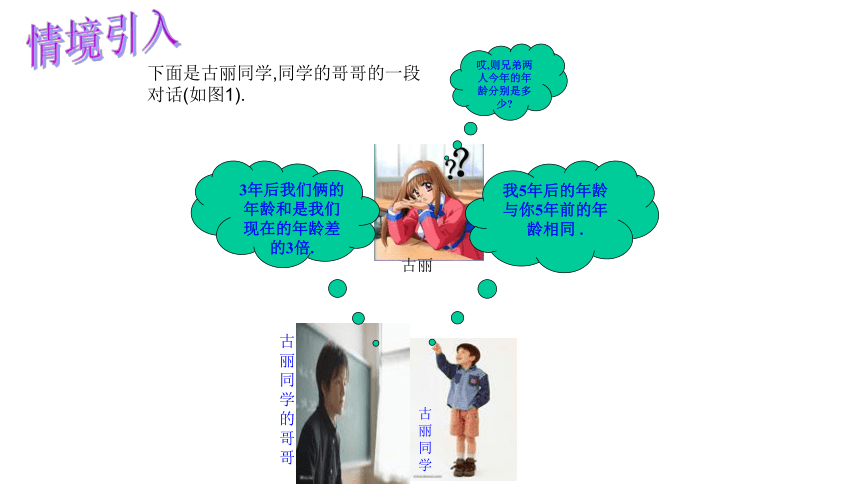
古丽同学
古丽同学的哥哥
?
?
古丽
3年后我们俩的年龄和是我们现在的年龄差的3倍.
我5年后的年龄与你5年前的年龄相同 .
哎,则兄弟两人今年的年龄分别是多少
下面是古丽同学,同学的哥哥的一段对话(如图1).
情境引入
解:设古丽的同学的哥哥年龄是y, 古丽的同学的年龄是 ⅹ.
割据题意列二元一次方程组,得
y-5=ⅹ+5
(Y+3)+(ⅹ+3) = 3 (y-ⅹ)
解二元一次方程组
y-5=ⅹ+5
(Y+3)+(ⅹ+3) = 3 (y-ⅹ)
y-ⅹ=5+5
Y+ⅹ- 3 y+3ⅹ =-6
-ⅹ+y=10 ① /×2
4ⅹ-2y =-6②
-2ⅹ+2y=20 ③
4ⅹ-2y =-6 ②
由② + ③,得
2ⅹ =14
解这个一元一次方程,得
ⅹ =7
把ⅹ =7代入③,得
y-7=10
y=17
所以这个二元一次方程组解:
ⅹ=7
y =17
答:古丽的同学的哥哥年龄是17,古丽的同学的年龄是 7.
养牛场原有30只大牛和15只小牛,1天约需要饲675kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
探究新知
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
解得:
20
5
化简得:
①
②
解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg.
依题意得
探新:根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售量(按瓶计算)比为2:5。某厂每天生产这种毒液22.5t,这些毒液应该分装大、小两种产品各多少瓶?
分析:问题中包含两个条件
大瓶数:小瓶数=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量
解:设这些消毒液应该分装x大瓶、y小瓶。
依题意,得
解这个方程组,得
答这些消毒液应该分装20000大瓶和50000小瓶
1、在捐款活动中本班一共捐款85元了,2名同学给10元,4名同学给5元,其他学生有些是给2元,有些是给1元了.(本班总共有33名学生)
那么你们帮我计算一下多少名同学给2元,多少名同学给1元
解:设2元给的同学ⅹ名, 1元给的同学y名.
根据问题的意思列方程组,得
2ⅹ+y+2×10+4×5=85
Y+ⅹ +4+2=33
简化为方程组,得
2ⅹ+y=45
Y+ⅹ=27
解方程组,得
ⅹ=18
Y=9
答:2元给的同学18名, 1元给的同学9名.
课堂练习
2、民间流传着这样的民谣:“一百和尚一百馍,大和尚一个吃三,小和尚三个吃一,多少大和尚多少小和尚”?你能通过计算求出答案吗?
解:设大和尚有x个,小和尚有y个,
x+ y = 100
3x +1/3y = 100
由题意得:
解这个方程组,得:
x = 25
y = 75
答:
大和尚有25个,小和尚有75个。
3、(古代问题)有甲,乙两个牧童,甲对乙说:“把你的羊给我1只,我的羊数就是你的2倍.”乙回答说:“最好还是把你的羊给我1只,我们的羊数就一样了.”两个牧童各有多少只羊
ⅹ+1=2(y-1)
ⅹ-1= y+1
ⅹ=7
y=5
用二元一次方程组解:
设:甲的样ⅹ只,甲的样y只.
y =5
解:由④ - ③ ,得
分析:方程③与 ④中ⅹ的系数是1,所以用加减法,比较简便。
把y =5代入④,得
ⅹ-5=2
解这个方程,得
ⅹ=7
所以这个方程组的解是
ⅹ=7
y =5
答:甲的有7只,乙的有5只.
ⅹ+1=2(y-1)
ⅹ-1= y+1
ⅹ+1=2(y-1) ①
ⅹ-1= y+1 ②
ⅹ+1=2y-2
ⅹ-1= y+1
ⅹ-2y=-2-1
ⅹ-y=1 +1
ⅹ-2y=-3 ③
ⅹ-y=2 ④
4、长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,
答:小明估计不准确.2米的应取8段,1米的 应取2段.
解得:
依题意得
提升自我
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680
2x+y=2280
解得:
x=960
y=360
(2)若7个餐厅同时开放,则有5×960+2×360=5320
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.
5320>5300
依题意得
某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排x10天精加工,5天粗加工.
拓展延伸
依题意得
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
课堂小结
8.3实际问题与二元一次方程组(1)
教学目标
(1)经历运用方程解决实际问题的过程,体会方程是刻画现实世界的有效数学模型.
教学重点与难点
难点:确定解题策略,比较估算与精确计算.
(2)能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程.
(3)学会比较估算与静确计算以及检验方程组的解是否符号合题意并正确作答.
(4)培养分析,解决问题的能力,体会二元一次方程组的应用价值,感受数学文化.
重点:以方程组为工具分析,解决含有多个未知数的实际问题..
列方程组解应用题的步骤:
审题
设未知数
列方程组
解方程组
检验
答
古丽同学
古丽同学的哥哥
?
?
古丽
3年后我们俩的年龄和是我们现在的年龄差的3倍.
我5年后的年龄与你5年前的年龄相同 .
哎,则兄弟两人今年的年龄分别是多少
下面是古丽同学,同学的哥哥的一段对话(如图1).
情境引入
解:设古丽的同学的哥哥年龄是y, 古丽的同学的年龄是 ⅹ.
割据题意列二元一次方程组,得
y-5=ⅹ+5
(Y+3)+(ⅹ+3) = 3 (y-ⅹ)
解二元一次方程组
y-5=ⅹ+5
(Y+3)+(ⅹ+3) = 3 (y-ⅹ)
y-ⅹ=5+5
Y+ⅹ- 3 y+3ⅹ =-6
-ⅹ+y=10 ① /×2
4ⅹ-2y =-6②
-2ⅹ+2y=20 ③
4ⅹ-2y =-6 ②
由② + ③,得
2ⅹ =14
解这个一元一次方程,得
ⅹ =7
把ⅹ =7代入③,得
y-7=10
y=17
所以这个二元一次方程组解:
ⅹ=7
y =17
答:古丽的同学的哥哥年龄是17,古丽的同学的年龄是 7.
养牛场原有30只大牛和15只小牛,1天约需要饲675kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
探究新知
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
解得:
20
5
化简得:
①
②
解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg.
依题意得
探新:根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售量(按瓶计算)比为2:5。某厂每天生产这种毒液22.5t,这些毒液应该分装大、小两种产品各多少瓶?
分析:问题中包含两个条件
大瓶数:小瓶数=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量
解:设这些消毒液应该分装x大瓶、y小瓶。
依题意,得
解这个方程组,得
答这些消毒液应该分装20000大瓶和50000小瓶
1、在捐款活动中本班一共捐款85元了,2名同学给10元,4名同学给5元,其他学生有些是给2元,有些是给1元了.(本班总共有33名学生)
那么你们帮我计算一下多少名同学给2元,多少名同学给1元
解:设2元给的同学ⅹ名, 1元给的同学y名.
根据问题的意思列方程组,得
2ⅹ+y+2×10+4×5=85
Y+ⅹ +4+2=33
简化为方程组,得
2ⅹ+y=45
Y+ⅹ=27
解方程组,得
ⅹ=18
Y=9
答:2元给的同学18名, 1元给的同学9名.
课堂练习
2、民间流传着这样的民谣:“一百和尚一百馍,大和尚一个吃三,小和尚三个吃一,多少大和尚多少小和尚”?你能通过计算求出答案吗?
解:设大和尚有x个,小和尚有y个,
x+ y = 100
3x +1/3y = 100
由题意得:
解这个方程组,得:
x = 25
y = 75
答:
大和尚有25个,小和尚有75个。
3、(古代问题)有甲,乙两个牧童,甲对乙说:“把你的羊给我1只,我的羊数就是你的2倍.”乙回答说:“最好还是把你的羊给我1只,我们的羊数就一样了.”两个牧童各有多少只羊
ⅹ+1=2(y-1)
ⅹ-1= y+1
ⅹ=7
y=5
用二元一次方程组解:
设:甲的样ⅹ只,甲的样y只.
y =5
解:由④ - ③ ,得
分析:方程③与 ④中ⅹ的系数是1,所以用加减法,比较简便。
把y =5代入④,得
ⅹ-5=2
解这个方程,得
ⅹ=7
所以这个方程组的解是
ⅹ=7
y =5
答:甲的有7只,乙的有5只.
ⅹ+1=2(y-1)
ⅹ-1= y+1
ⅹ+1=2(y-1) ①
ⅹ-1= y+1 ②
ⅹ+1=2y-2
ⅹ-1= y+1
ⅹ-2y=-2-1
ⅹ-y=1 +1
ⅹ-2y=-3 ③
ⅹ-y=2 ④
4、长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,
答:小明估计不准确.2米的应取8段,1米的 应取2段.
解得:
依题意得
提升自我
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680
2x+y=2280
解得:
x=960
y=360
(2)若7个餐厅同时开放,则有5×960+2×360=5320
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.
5320>5300
依题意得
某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?
解:设该公司应安排x天精加工,y天粗加工,
x+y=15
6x+16y=140
解 得:
x=10
y=5
答:该公司应安排x10天精加工,5天粗加工.
拓展延伸
依题意得
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
课堂小结
