人教版八年级数学上册13.1.2线段的垂直平分线的性质(第二课时)课件 (共26张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1.2线段的垂直平分线的性质(第二课时)课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 503.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 07:32:26 | ||
图片预览



文档简介
(共26张PPT)
八年级—人教版—数学—第十三章
13.1.2线段的垂直平分线的性质(第二课时)
学习目标
1.能用尺规作出已知线段的垂直平分线;
2.进一步了解尺规作图的一般步骤和作图语言,理解
作图的依据;
3.能用尺规作出已知轴对称图形的对称轴;
4.能够运用尺规作图的方法解决简单的作图问题.
学习重点
能够运用尺规作图的方法解决简单的作图问题.
复习回顾:线段垂直平分线的有关性质.
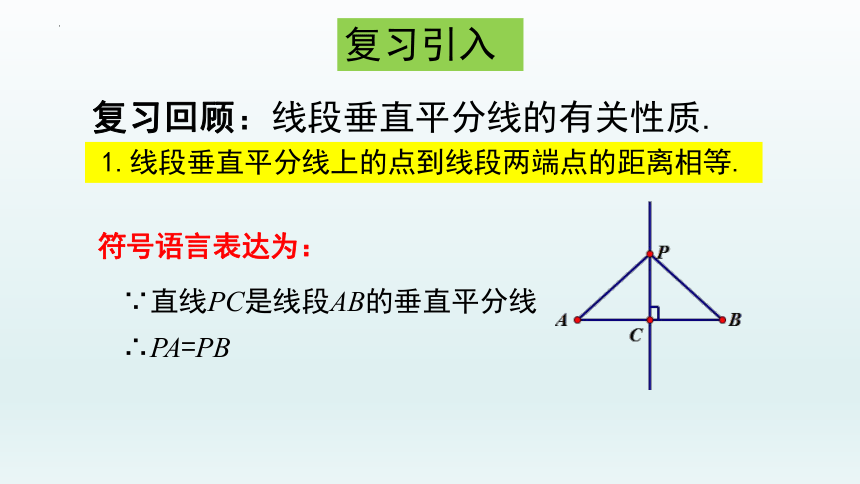
1.线段垂直平分线上的点到线段两端点的距离相等.
复习引入
符号语言表达为:
∵直线PC是线段AB的垂直平分线
∴PA=PB
复习回顾:线段垂直平分线的有关性质.
复习引入
符号语言表达为:
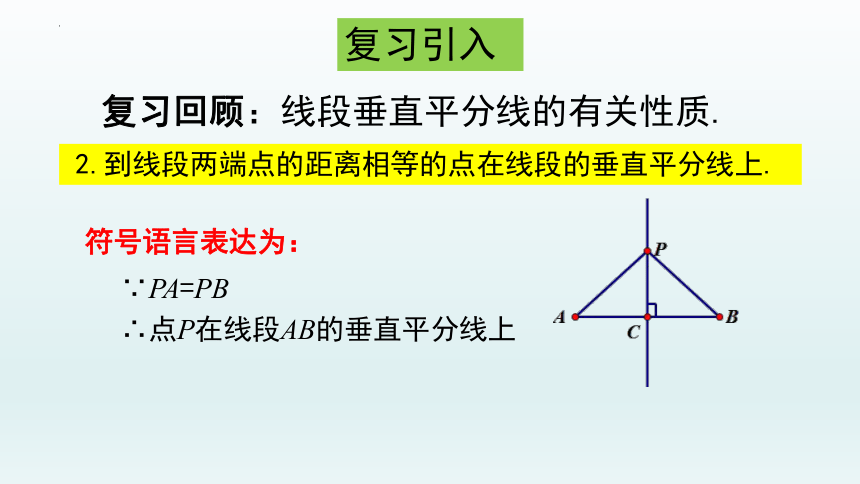
2.到线段两端点的距离相等的点在线段的垂直平分线上.
∵PA=PB
∴点P在线段AB的垂直平分线上
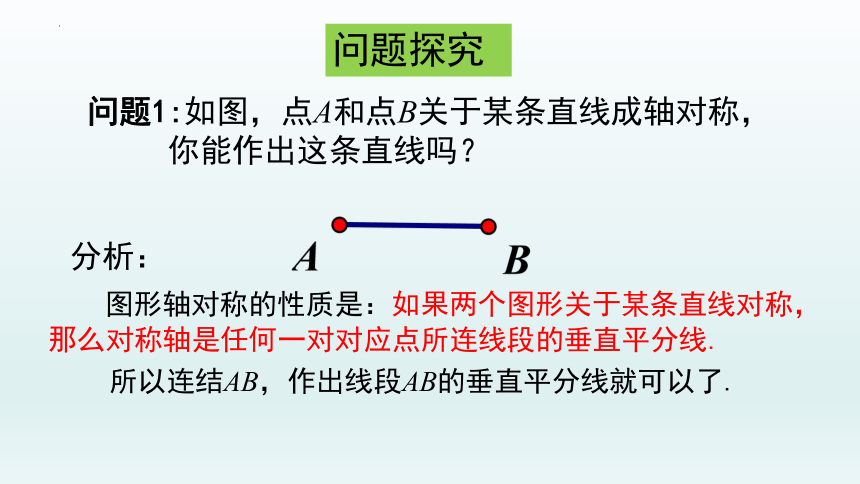
问题1:如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
分析:
图形轴对称的性质是:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
所以连结AB,作出线段AB的垂直平分线就可以了.
问题探究
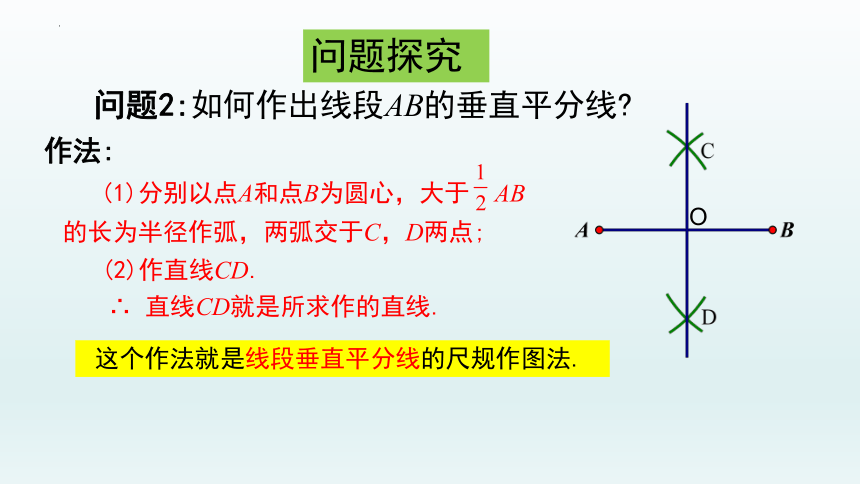
问题2:如何作出线段AB的垂直平分线呢
分析:
问题探究
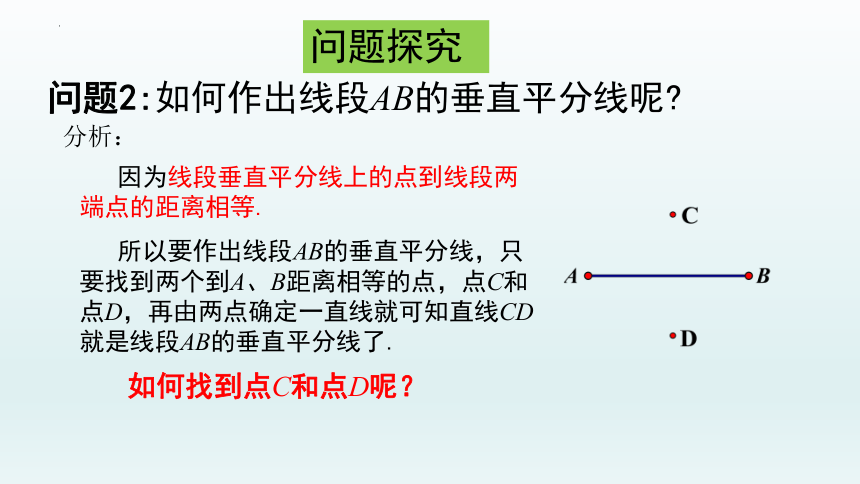
因为线段垂直平分线上的点到线段两端点的距离相等.
所以要作出线段AB的垂直平分线,只要找到两个到A、B距离相等的点,点C和点D,再由两点确定一直线就可知直线CD就是线段AB的垂直平分线了.
如何找到点C和点D呢?
问题2:如何作出线段的垂直平分线
分析:
连结CA、CB、DA、DB,
则CA=CB,DA=DB.
为了方便,我们使作点C和作点D时所取的半径相等,这样作一次弧就可以同时得到点C和点D了.再由两点确定一直线可知:直线CD就是所求作的线段AB的垂直平分线了.
问题探究
因为CA=CB,所以分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交就可以找到点C了.同样的方法可以找到点D.
问题2:如何作出线段AB的垂直平分线
作法:
(2)作直线CD.
(1)分别以点A和点B为圆心,大于 AB
的长为半径作弧,两弧交于C,D两点;
∴ 直线CD就是所求作的直线.
O
问题探究
这个作法就是线段垂直平分线的尺规作图法.
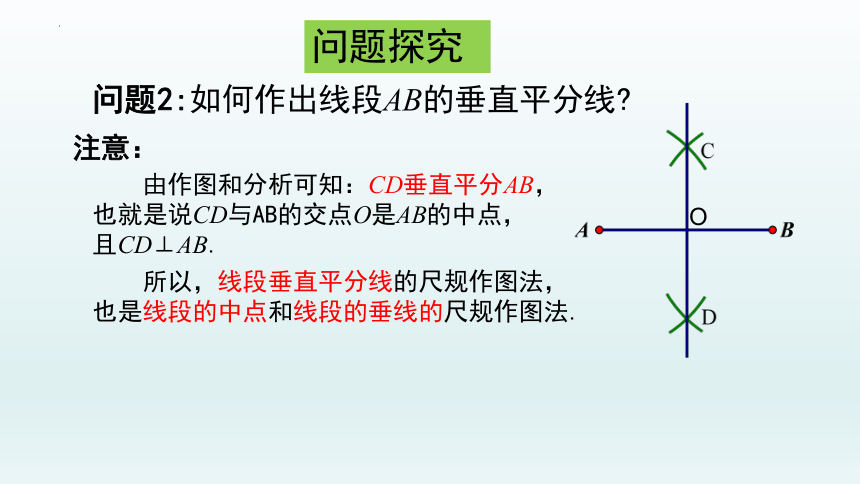
问题2:如何作出线段AB的垂直平分线
注意:
O
由作图和分析可知:CD垂直平分AB,
也就是说CD与AB的交点O是AB的中点,
且CD⊥AB.
所以,线段垂直平分线的尺规作图法,也是线段的中点和线段的垂线的尺规作图法.
问题探究
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
分析:
观察上一探究的图形,我们可以发
现:点C相当于上一探究中CD上的一点.
D E
例题讲解
只要我们找到上一探究中AB对应的
线段DE,然后作出线段DE的垂直平分线
就可以了.
求作:AB的垂线,使它经过点C.
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
分析:
所以任意取一点K,使点K和点C在AB的两旁;
这时CD=CE,点C就在线段DE的垂直平分线上.
例题讲解
接着再作DF=EF,则点F也在线段DE的垂直平分
线上.
由两点确定一直线知:
直线CF就是线段DE的垂直平分线,所以CF⊥AB.
以点C为圆心,CK的长为半径作弧,交AB于点
D和点E,则DE为探究中AB对应的线段了.
求作:AB的垂线,使它经过点C.
变式:
问:如果点C在直线AB上,
那么过点C怎样作出AB的垂线?
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(4)作直线CF.
∴ 直线CF就是所求作的垂线.
(2)以点C为圆心,CK的长为半径作弧,交
AB于点D和点E.
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
例题讲解
求作:AB的垂线,使它经过点C.
(3)分别以点D和点E为圆心,大于 DE的长
为半径作弧,两弧交于点F.
已知:直线AB和AB上一点C(如图)
问:若点C在直线AB上,那么过点C怎样作出AB的垂线?
分析:
同样找到例题中的线段DE就可以了.
D E
变式练习
求作:AB的垂线,使它经过点C.
这时以点C为圆心,任意长为半径
作弧,交AB于点D和点E,就可以得到
例题中的线段DE了.
已知:直线AB和AB上一点C(如图)
求作:AB的垂线,使它经过点C.
问:若点C在直线AB上,那过点C怎样作出AB的垂线?
作法:
(1)以点C为圆心,任意长为半径作弧,
交AB于点D和点E;
∴ 直线CF即为所求作的垂线.
(3)作直线CF.
变式练习
D
E
(2)分别以点D和点E为圆心,大于 DE
的长为半径作弧,两弧交于点F.
(1)经过已知直线外一点
作这条直线的垂线
(2)经过已知直线上一点
作这条直线的垂线
归纳:这两种情况就是“经过一点作已知直线的垂线”
的所有情况.
例1
变式练习
1.如图,已知点A、点B以及直线l.用尺规作图的方法在直线l上
求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
分析:
因为要使PA=PB,所以点P在线段AB的垂直平分线上;
∴ 点P为所求作的点.
课堂练习
因为又要满足点P在直线l上,所以点P为线段AB的垂直平分线与直线l的交点.
2.如图,小河边有两个村庄,要在河岸边建一自来水厂向A村与B
村供水,若要使厂部到A,B的距离相等,则应选在哪里
分析:
因为要使厂部到A,B的距离相等,所以厂部在线段AB的垂直平分线上;
∴ 点P就是厂部应选的位置.
课堂练习
因为厂部又要在河岸边建,因此厂部为线段AB的垂直平分线与河岸CD的交点.
3.如图,某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,
OB表示公路,现计划修建一座仓库,希望仓库到两所大学的距离相等,
到两条公路的距离也相等,你能确定出仓库P应该建在什么位置吗?请
在图中画出点P的位置(保留作图痕迹,不要求写出作法).
分析:
因为要满足仓库到两所大学的距离相等,所以仓库在线段MN的垂直平分线上;
因为又要满足仓库到两条公路的距离相等,所以仓库在∠AOB的平分线上;
因此,仓库P为线段MN的垂直平分线与∠AOB的平分线的交点.
∴ 点P就是仓库应选的位置.
课堂练习
PA=PB
第1题
第2题
第3题
厂部到A,B的距离相等
仓库到两所大学
的距离相等
三题都是要作一点到两点距离相等的意思
所以都可以通过作线段的垂直平分线来解决.
归纳:
作一点到两点距离相等则作线段的垂直平分线
仓库到两条公路
的距离相等
作一点到角两边的距离相等则作角的平分线
仓库到两所大学
的距离相等
区分
4.尺规作图:
如图,五角星是轴对称图形,请作出它的一条对称轴.
分析:
所以找出这个五角星的一对对应点A和B,
连结AB,作出线段AB的垂直平分线m,则直
线m就是这个五角星的一条对称轴.
因为轴对称图形的对称轴,是任何一对
对应点所连线段的垂直平分线.
∴ 直线m即为所求作的一条对称轴.
m
课堂练习
类似地,你能作出这个五角星的其他对称轴吗?
归纳:作轴对称图形的一条对称轴的步骤
所以:直线m就是轴对称图形的一条对称轴.
(1)找出轴对称图形的一对对应点A和B;
(2)连结AB;
(3)作出线段AB的垂直平分线m.
m
5.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴
一样吗?
分析:
跟五角星一样,找出每个图形的一对对应点A和B,作出线段AB
的垂直平分线m,则直线m就是所求作的一条对称轴了.
课堂练习
B
C
D
A
5.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴
一样吗?
课堂练习
归纳:
轴对称图形的对称轴可能是一条,也可能是两条,还可能
是三条、四条甚至是无数条.轴对称图形的对称轴的条数是由
图形本身的特点决定的,不一定是唯一的.
B
C
D
A
线段的垂直平分线的性质(第二课时)
用尺规作图作线段垂直平分线
作轴对称图形的对称轴
这是作对称轴的重要方法,也是作线段的中点和直线的垂线的方法.
课堂小结
课本P64:
1.练习2
2.习题13.1复习巩固第2题
课后作业
谢 谢 !
课堂到此结束
八年级—人教版—数学—第十三章
13.1.2线段的垂直平分线的性质(第二课时)
学习目标
1.能用尺规作出已知线段的垂直平分线;
2.进一步了解尺规作图的一般步骤和作图语言,理解
作图的依据;
3.能用尺规作出已知轴对称图形的对称轴;
4.能够运用尺规作图的方法解决简单的作图问题.
学习重点
能够运用尺规作图的方法解决简单的作图问题.
复习回顾:线段垂直平分线的有关性质.
1.线段垂直平分线上的点到线段两端点的距离相等.
复习引入
符号语言表达为:
∵直线PC是线段AB的垂直平分线
∴PA=PB
复习回顾:线段垂直平分线的有关性质.
复习引入
符号语言表达为:
2.到线段两端点的距离相等的点在线段的垂直平分线上.
∵PA=PB
∴点P在线段AB的垂直平分线上
问题1:如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
分析:
图形轴对称的性质是:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
所以连结AB,作出线段AB的垂直平分线就可以了.
问题探究
问题2:如何作出线段AB的垂直平分线呢
分析:
问题探究
因为线段垂直平分线上的点到线段两端点的距离相等.
所以要作出线段AB的垂直平分线,只要找到两个到A、B距离相等的点,点C和点D,再由两点确定一直线就可知直线CD就是线段AB的垂直平分线了.
如何找到点C和点D呢?
问题2:如何作出线段的垂直平分线
分析:
连结CA、CB、DA、DB,
则CA=CB,DA=DB.
为了方便,我们使作点C和作点D时所取的半径相等,这样作一次弧就可以同时得到点C和点D了.再由两点确定一直线可知:直线CD就是所求作的线段AB的垂直平分线了.
问题探究
因为CA=CB,所以分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交就可以找到点C了.同样的方法可以找到点D.
问题2:如何作出线段AB的垂直平分线
作法:
(2)作直线CD.
(1)分别以点A和点B为圆心,大于 AB
的长为半径作弧,两弧交于C,D两点;
∴ 直线CD就是所求作的直线.
O
问题探究
这个作法就是线段垂直平分线的尺规作图法.
问题2:如何作出线段AB的垂直平分线
注意:
O
由作图和分析可知:CD垂直平分AB,
也就是说CD与AB的交点O是AB的中点,
且CD⊥AB.
所以,线段垂直平分线的尺规作图法,也是线段的中点和线段的垂线的尺规作图法.
问题探究
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
分析:
观察上一探究的图形,我们可以发
现:点C相当于上一探究中CD上的一点.
D E
例题讲解
只要我们找到上一探究中AB对应的
线段DE,然后作出线段DE的垂直平分线
就可以了.
求作:AB的垂线,使它经过点C.
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
分析:
所以任意取一点K,使点K和点C在AB的两旁;
这时CD=CE,点C就在线段DE的垂直平分线上.
例题讲解
接着再作DF=EF,则点F也在线段DE的垂直平分
线上.
由两点确定一直线知:
直线CF就是线段DE的垂直平分线,所以CF⊥AB.
以点C为圆心,CK的长为半径作弧,交AB于点
D和点E,则DE为探究中AB对应的线段了.
求作:AB的垂线,使它经过点C.
变式:
问:如果点C在直线AB上,
那么过点C怎样作出AB的垂线?
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(4)作直线CF.
∴ 直线CF就是所求作的垂线.
(2)以点C为圆心,CK的长为半径作弧,交
AB于点D和点E.
例1:尺规作图:经过已知直线外一点作这条直线的垂线
已知:直线AB和AB外一点C(如图)
例题讲解
求作:AB的垂线,使它经过点C.
(3)分别以点D和点E为圆心,大于 DE的长
为半径作弧,两弧交于点F.
已知:直线AB和AB上一点C(如图)
问:若点C在直线AB上,那么过点C怎样作出AB的垂线?
分析:
同样找到例题中的线段DE就可以了.
D E
变式练习
求作:AB的垂线,使它经过点C.
这时以点C为圆心,任意长为半径
作弧,交AB于点D和点E,就可以得到
例题中的线段DE了.
已知:直线AB和AB上一点C(如图)
求作:AB的垂线,使它经过点C.
问:若点C在直线AB上,那过点C怎样作出AB的垂线?
作法:
(1)以点C为圆心,任意长为半径作弧,
交AB于点D和点E;
∴ 直线CF即为所求作的垂线.
(3)作直线CF.
变式练习
D
E
(2)分别以点D和点E为圆心,大于 DE
的长为半径作弧,两弧交于点F.
(1)经过已知直线外一点
作这条直线的垂线
(2)经过已知直线上一点
作这条直线的垂线
归纳:这两种情况就是“经过一点作已知直线的垂线”
的所有情况.
例1
变式练习
1.如图,已知点A、点B以及直线l.用尺规作图的方法在直线l上
求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
分析:
因为要使PA=PB,所以点P在线段AB的垂直平分线上;
∴ 点P为所求作的点.
课堂练习
因为又要满足点P在直线l上,所以点P为线段AB的垂直平分线与直线l的交点.
2.如图,小河边有两个村庄,要在河岸边建一自来水厂向A村与B
村供水,若要使厂部到A,B的距离相等,则应选在哪里
分析:
因为要使厂部到A,B的距离相等,所以厂部在线段AB的垂直平分线上;
∴ 点P就是厂部应选的位置.
课堂练习
因为厂部又要在河岸边建,因此厂部为线段AB的垂直平分线与河岸CD的交点.
3.如图,某地有两所大学和两条交叉的公路.图中点M,N表示大学,OA,
OB表示公路,现计划修建一座仓库,希望仓库到两所大学的距离相等,
到两条公路的距离也相等,你能确定出仓库P应该建在什么位置吗?请
在图中画出点P的位置(保留作图痕迹,不要求写出作法).
分析:
因为要满足仓库到两所大学的距离相等,所以仓库在线段MN的垂直平分线上;
因为又要满足仓库到两条公路的距离相等,所以仓库在∠AOB的平分线上;
因此,仓库P为线段MN的垂直平分线与∠AOB的平分线的交点.
∴ 点P就是仓库应选的位置.
课堂练习
PA=PB
第1题
第2题
第3题
厂部到A,B的距离相等
仓库到两所大学
的距离相等
三题都是要作一点到两点距离相等的意思
所以都可以通过作线段的垂直平分线来解决.
归纳:
作一点到两点距离相等则作线段的垂直平分线
仓库到两条公路
的距离相等
作一点到角两边的距离相等则作角的平分线
仓库到两所大学
的距离相等
区分
4.尺规作图:
如图,五角星是轴对称图形,请作出它的一条对称轴.
分析:
所以找出这个五角星的一对对应点A和B,
连结AB,作出线段AB的垂直平分线m,则直
线m就是这个五角星的一条对称轴.
因为轴对称图形的对称轴,是任何一对
对应点所连线段的垂直平分线.
∴ 直线m即为所求作的一条对称轴.
m
课堂练习
类似地,你能作出这个五角星的其他对称轴吗?
归纳:作轴对称图形的一条对称轴的步骤
所以:直线m就是轴对称图形的一条对称轴.
(1)找出轴对称图形的一对对应点A和B;
(2)连结AB;
(3)作出线段AB的垂直平分线m.
m
5.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴
一样吗?
分析:
跟五角星一样,找出每个图形的一对对应点A和B,作出线段AB
的垂直平分线m,则直线m就是所求作的一条对称轴了.
课堂练习
B
C
D
A
5.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴
一样吗?
课堂练习
归纳:
轴对称图形的对称轴可能是一条,也可能是两条,还可能
是三条、四条甚至是无数条.轴对称图形的对称轴的条数是由
图形本身的特点决定的,不一定是唯一的.
B
C
D
A
线段的垂直平分线的性质(第二课时)
用尺规作图作线段垂直平分线
作轴对称图形的对称轴
这是作对称轴的重要方法,也是作线段的中点和直线的垂线的方法.
课堂小结
课本P64:
1.练习2
2.习题13.1复习巩固第2题
课后作业
谢 谢 !
课堂到此结束
