人教版八年级上册13.3.2等边三角形(第二课时)课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.2等边三角形(第二课时)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 08:16:16 | ||
图片预览






文档简介
(共20张PPT)
八年级—人教版—数学—十三章
13.3.2 等边三角形(第二课时)
学习目标:
(1)理解掌握有一个角为30°的直角三角形的性质及其简单应用。
(2)经历“观察—猜想—验证—证明”的过程,感受数学的严谨性。
学习重点:
含30°角的直角三角形的性质的发现与应用。
课前准备
两个全等的含30°角的三角尺.
复习旧知
1. 等边三角形的定义:
三边都相等的三角形为等边三角形.
2. 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等于60°.
3. 等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
探究活动
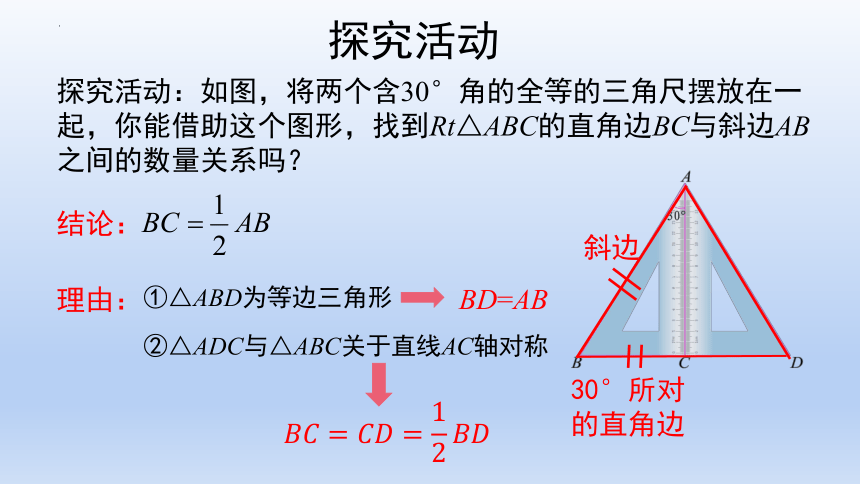
探究活动:如图,将两个含30°角的全等的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
结论:
理由:
①△ABD为等边三角形
②△ADC与△ABC关于直线AC轴对称
BD=AB
斜边
30°所对
的直角边
结论证明
从探究活动可得到结论:
在直角三角形中,30°角所对的直角边是斜边的一半。
下面我们将证明这个结论的正确性。
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
★转化思想
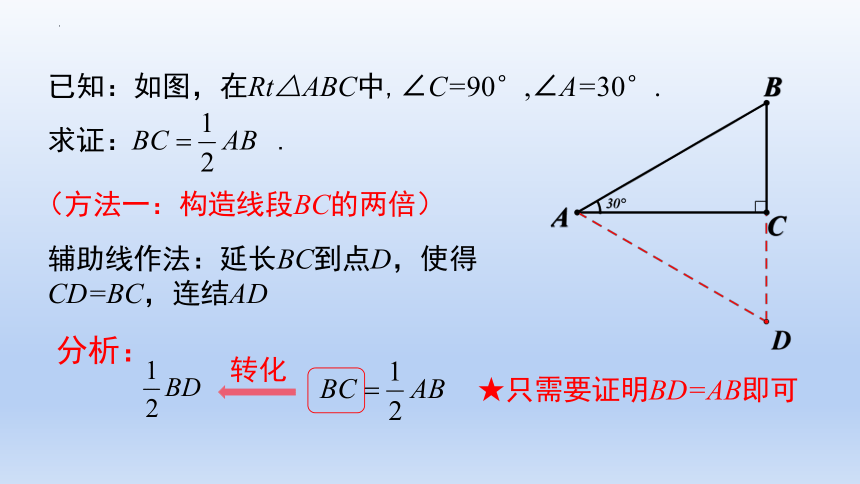
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
(方法一:构造线段BC的两倍)
辅助线作法:延长BC到点D,使得CD=BC,连结AD
求证: .
转化
分析:
★只需要证明BD=AB即可
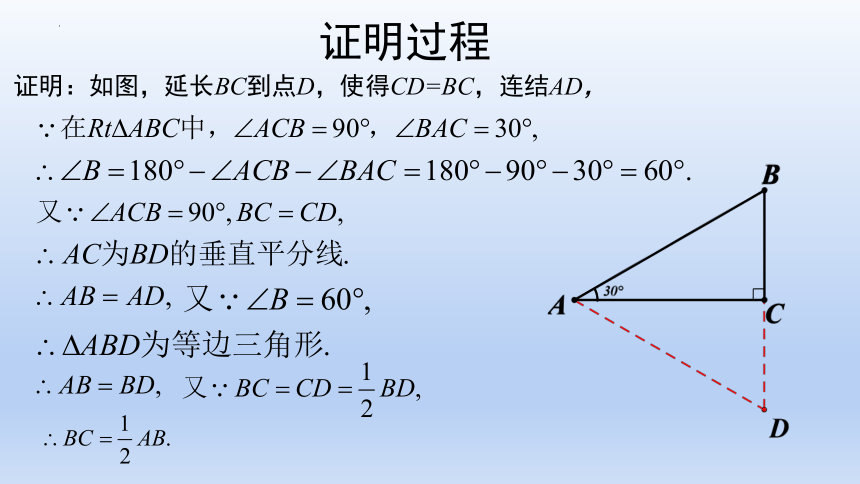
证明过程
证明:如图,延长BC到点D,使得CD=BC,连结AD,
(方法二:构造线段AB的一半)
D
辅助法的作法:作AB的中点D,连结CD,
★只需要证明BC=BD即可
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
分析:
转化
暂时不能证明
(换一种思路:在线段AB上截取BD=BC,连结CD)
分析:
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
转化
★只需要证明点D为AB的中点即可
证明过程
证明:如图,在线段AB上截取BD=BC,连结CD,
含30°角的直角三角形的性质定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
符号语言:
若 Rt△ABC中,∠C=90°,∠A=30°
得出定理
综合应用
例题:如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
分析:要求BC,DE的长度必须要找准这两条线段落在那两个直角三角形中,
求BC
Rt△ABC
求DE
Rt△ADE
解题过程
答:立柱BC的长是3.7m,DE的长是1.85m.
课堂小结
1.通过自己的探索发现了含30°角的直角三角形有什么特殊的性质?
2.它解决了什么问题?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中的有关线段长度的计算问题.
问题一:含30°角的直角三角形的性质可以解决什么问题?
答:
直角三角形中的角与角之间的关系
直角三角形中的边与边之间的关系
1. 含30°的直角三角形
2. 含45°的直角三角形
特殊角:15°、60°、120°、150°
特殊角:135°
例:如图,在Rt△ABC中,∠C=90°,∠A=15°,BC=10,AB的垂直平分线交AC于点D,则AD=_________
分析:
20
转化
BDC
问题二:在证明30°的直角三角形的性质定理中用到了哪些添加辅助线的方法呢?
1.补短法:如图1中,通过延长BC到
点D,使得CD=BC.
2.截长法:如图2中,截取BD=BC
或作线段AB的中点D.
答:
特别地,当刚好出现的是2倍关系的时候,延长的线段刚好与之相等,或者截取的线段刚好是它的一半时,我们也称这种添加辅助线的方法为“倍长中线法”.
“截长补短法”和“倍长中线法”是添加辅助线的常用方法,适合于证明线段的和、差、倍、分等类型的题目.
谢 谢
八年级—人教版—数学—十三章
13.3.2 等边三角形(第二课时)
学习目标:
(1)理解掌握有一个角为30°的直角三角形的性质及其简单应用。
(2)经历“观察—猜想—验证—证明”的过程,感受数学的严谨性。
学习重点:
含30°角的直角三角形的性质的发现与应用。
课前准备
两个全等的含30°角的三角尺.
复习旧知
1. 等边三角形的定义:
三边都相等的三角形为等边三角形.
2. 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等于60°.
3. 等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
探究活动
探究活动:如图,将两个含30°角的全等的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
结论:
理由:
①△ABD为等边三角形
②△ADC与△ABC关于直线AC轴对称
BD=AB
斜边
30°所对
的直角边
结论证明
从探究活动可得到结论:
在直角三角形中,30°角所对的直角边是斜边的一半。
下面我们将证明这个结论的正确性。
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
★转化思想
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
(方法一:构造线段BC的两倍)
辅助线作法:延长BC到点D,使得CD=BC,连结AD
求证: .
转化
分析:
★只需要证明BD=AB即可
证明过程
证明:如图,延长BC到点D,使得CD=BC,连结AD,
(方法二:构造线段AB的一半)
D
辅助法的作法:作AB的中点D,连结CD,
★只需要证明BC=BD即可
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
分析:
转化
暂时不能证明
(换一种思路:在线段AB上截取BD=BC,连结CD)
分析:
已知:如图,在Rt△ABC中,∠C=90°,∠A=30°.
求证: .
转化
★只需要证明点D为AB的中点即可
证明过程
证明:如图,在线段AB上截取BD=BC,连结CD,
含30°角的直角三角形的性质定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
符号语言:
若 Rt△ABC中,∠C=90°,∠A=30°
得出定理
综合应用
例题:如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC,DE要多长?
分析:要求BC,DE的长度必须要找准这两条线段落在那两个直角三角形中,
求BC
Rt△ABC
求DE
Rt△ADE
解题过程
答:立柱BC的长是3.7m,DE的长是1.85m.
课堂小结
1.通过自己的探索发现了含30°角的直角三角形有什么特殊的性质?
2.它解决了什么问题?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中的有关线段长度的计算问题.
问题一:含30°角的直角三角形的性质可以解决什么问题?
答:
直角三角形中的角与角之间的关系
直角三角形中的边与边之间的关系
1. 含30°的直角三角形
2. 含45°的直角三角形
特殊角:15°、60°、120°、150°
特殊角:135°
例:如图,在Rt△ABC中,∠C=90°,∠A=15°,BC=10,AB的垂直平分线交AC于点D,则AD=_________
分析:
20
转化
BDC
问题二:在证明30°的直角三角形的性质定理中用到了哪些添加辅助线的方法呢?
1.补短法:如图1中,通过延长BC到
点D,使得CD=BC.
2.截长法:如图2中,截取BD=BC
或作线段AB的中点D.
答:
特别地,当刚好出现的是2倍关系的时候,延长的线段刚好与之相等,或者截取的线段刚好是它的一半时,我们也称这种添加辅助线的方法为“倍长中线法”.
“截长补短法”和“倍长中线法”是添加辅助线的常用方法,适合于证明线段的和、差、倍、分等类型的题目.
谢 谢
