人教版八年级上册15.3分式方程课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册15.3分式方程课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 08:08:10 | ||
图片预览






文档简介
(共18张PPT)
八年级—人教版—数学—第十五章
分式方程的应用
学习目标
会列分式方程解决简单的实际问题,并理解要进行两方面的检验:检验所求得的未知数的值是否为所列方程的根;检验方程的根是否符合题意.
2.行程问题
基本公式:路程=速度×时间
1.工程问题
基本公式:工作量=工效×工时
一、温故知新
练习:
(1)一项工作甲单独做 天完成,乙单独做 天完成. 甲的工作效
率是 ,乙的工作效率是 ,甲、乙合作5天,一共完成工
程的 .
(2)甲乙两地相距 千米,客车的速度为 千米/时,则乘坐该
客车从甲地到乙地需_________小时.
一、温故知新
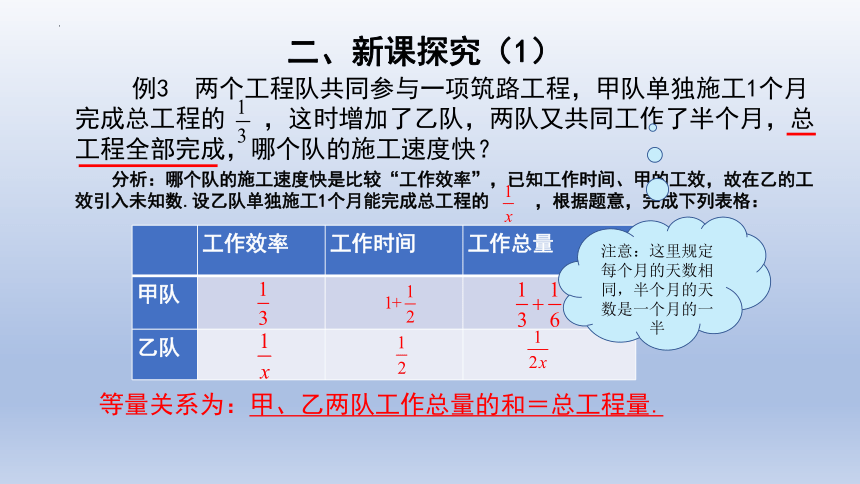
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
工作效率 工作时间 工作总量
甲队
乙队
分析:哪个队的施工速度快是比较“工作效率”,已知工作时间、甲的工效,故在乙的工效引入未知数.设乙队单独施工1个月能完成总工程的 ,根据题意,完成下列表格:
等量关系为:甲、乙两队工作总量的和=总工程量.
二、新课探究(1)
注意:这里规定每个月的天数相同,半个月的天数是一个月的一半
解:设乙队单独施工1个月完成总工程的 .记总工程量为1,根据工程的实际进度,列方程得
解得
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队单独施工速度快.
方程两边同时乘以 ,得
检验:当 时,
所以,原分式方程的解为
二、新课探究(1)
审
设
解
验
答
列
甲、乙两人合做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用时间相等.求甲、乙两人每小时各做零件多少个.
分析:设乙每小时做 个零件,根据题意,完成下列表格:
工作效率 工作时间 工作总量
甲
乙
90
60
变式练习一
等量关系为:甲所用的时间=乙所用的时间
解:设乙每小时做 个零件,根据题意,得
解得
检验:当 时,
所以,原分式方程的解为
答:甲每小时做18个零件,乙每小时做12 个零件.
变式练习一
例4 某次列车平均提速 km/h,用相同的时间,列车提速前行驶 km,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
分析:设提速前列车的平均速度为 km/h,根据题意,完成下列表格:
注意:这里的 表示已知数据
路程 速度 时间
提速前
提速后
等量关系为:列车提速前行驶的时间=列车提速后行驶的时间
二、新课探究(2)
解:设提速前列车的平均速度为 km/h,根据题意,得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
.
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
二、新课探究(2)
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20min到达目的地.求甲乙两人的速度.
路程 速度 时间
甲
乙
6
10
分析:设甲的速度为 km/h,根据题意,完成下列表格:
等量关系为:甲所用的时间=乙所用的时间-20分钟
变式练习二
解:设甲的速度为 km/h ,乙的速度为 km/h,根据题意,得
解得
.
经检验:
所以,原分式方程的解为
答:甲的速度为 km/h ,乙的速度为6 km/h.
变式练习二
是原分式方程的解.
课堂小结:通过本节课的学习,你有什么收获?
列分式方程解应用题的步骤:
(6)答:写出答案(要有单位).
(5)验:看方程的解是否满足方程和符合题意;
(4)解:解方程;
(3)列:根据等量关系,列出相应的分式方程;
(2)设:设未知数(要有单位);
(1)审:审清题意,了解已知量与所求量各是什么,找出等量关系;
例题4
解:设提速前列车的平均速度为 km/h,由题意得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
.
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
问题1
如何列分式方程来解应用题?
列分式方程来解应用题简单地可以概括为:审、设、列、解、验、答这六个步骤.审:审清题意,了解已知量与所求量各是什么,找出等量关系,是这六个步骤中最关键的,也是一个难点.因此,只要找出题目中的等量关系,那么后面的问题就迎刃而解了.
问题2 列分式方程解应用题时,如何找出题目中的等量关系?
列分式方程解应用题最关键的步骤是审题,也就是找出题目当中的等量关系,那如何正确地找出等量关系呢?最主要有以下三点:
1.牢记公式,根据公式来找等量关系.例如长方形、正方形的周长和面积公式.
2.熟记数量关系,根据数量关系找等量关系,比如工程问题、行程问题、销售问题、利润问题等等.
1.工程问题
数量关系:工作量=工效×工时
2.行程问题
数量关系:路程=速度×时间
3.销售问题
数量关系:总价=单价×数量
4.利润问题
数量关系:利润=收入-成本
3.抓住关键字词,根据字词的提示找等量关系.
问题3 列分式方程解应用题与列一元一次方程解应用题有何不同?
列分式方程解应用题与列一元一次方程解应用题的步骤大体相同,但是也要注意以下三个问题:
1.列分式方程解应用题的关键是用公式表示一些基本的数量关系;
解:设提速前列车的平均速度为 km/h,
由题意得
方程两边乘 ,得
解得
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
x(x+v)
s(x+v)=x(s+50).
2.列分式方程解应用题一定要验根,先检验方程的解是不是分式方程的解;若是分式方程的解,再检验这个解是否符合题意;
3.列分式方程解应用题要注意题目中的量的单位要统一.
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度
比是3:4,结果甲比乙提前20min到达目的地.求甲乙的速度.
变式练习二
等量关系为:甲所用的时间=乙所用的时间-20分钟
八年级—人教版—数学—第十五章
分式方程的应用
学习目标
会列分式方程解决简单的实际问题,并理解要进行两方面的检验:检验所求得的未知数的值是否为所列方程的根;检验方程的根是否符合题意.
2.行程问题
基本公式:路程=速度×时间
1.工程问题
基本公式:工作量=工效×工时
一、温故知新
练习:
(1)一项工作甲单独做 天完成,乙单独做 天完成. 甲的工作效
率是 ,乙的工作效率是 ,甲、乙合作5天,一共完成工
程的 .
(2)甲乙两地相距 千米,客车的速度为 千米/时,则乘坐该
客车从甲地到乙地需_________小时.
一、温故知新
例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
工作效率 工作时间 工作总量
甲队
乙队
分析:哪个队的施工速度快是比较“工作效率”,已知工作时间、甲的工效,故在乙的工效引入未知数.设乙队单独施工1个月能完成总工程的 ,根据题意,完成下列表格:
等量关系为:甲、乙两队工作总量的和=总工程量.
二、新课探究(1)
注意:这里规定每个月的天数相同,半个月的天数是一个月的一半
解:设乙队单独施工1个月完成总工程的 .记总工程量为1,根据工程的实际进度,列方程得
解得
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队单独施工速度快.
方程两边同时乘以 ,得
检验:当 时,
所以,原分式方程的解为
二、新课探究(1)
审
设
解
验
答
列
甲、乙两人合做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用时间相等.求甲、乙两人每小时各做零件多少个.
分析:设乙每小时做 个零件,根据题意,完成下列表格:
工作效率 工作时间 工作总量
甲
乙
90
60
变式练习一
等量关系为:甲所用的时间=乙所用的时间
解:设乙每小时做 个零件,根据题意,得
解得
检验:当 时,
所以,原分式方程的解为
答:甲每小时做18个零件,乙每小时做12 个零件.
变式练习一
例4 某次列车平均提速 km/h,用相同的时间,列车提速前行驶 km,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
分析:设提速前列车的平均速度为 km/h,根据题意,完成下列表格:
注意:这里的 表示已知数据
路程 速度 时间
提速前
提速后
等量关系为:列车提速前行驶的时间=列车提速后行驶的时间
二、新课探究(2)
解:设提速前列车的平均速度为 km/h,根据题意,得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
.
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
二、新课探究(2)
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20min到达目的地.求甲乙两人的速度.
路程 速度 时间
甲
乙
6
10
分析:设甲的速度为 km/h,根据题意,完成下列表格:
等量关系为:甲所用的时间=乙所用的时间-20分钟
变式练习二
解:设甲的速度为 km/h ,乙的速度为 km/h,根据题意,得
解得
.
经检验:
所以,原分式方程的解为
答:甲的速度为 km/h ,乙的速度为6 km/h.
变式练习二
是原分式方程的解.
课堂小结:通过本节课的学习,你有什么收获?
列分式方程解应用题的步骤:
(6)答:写出答案(要有单位).
(5)验:看方程的解是否满足方程和符合题意;
(4)解:解方程;
(3)列:根据等量关系,列出相应的分式方程;
(2)设:设未知数(要有单位);
(1)审:审清题意,了解已知量与所求量各是什么,找出等量关系;
例题4
解:设提速前列车的平均速度为 km/h,由题意得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
.
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
问题1
如何列分式方程来解应用题?
列分式方程来解应用题简单地可以概括为:审、设、列、解、验、答这六个步骤.审:审清题意,了解已知量与所求量各是什么,找出等量关系,是这六个步骤中最关键的,也是一个难点.因此,只要找出题目中的等量关系,那么后面的问题就迎刃而解了.
问题2 列分式方程解应用题时,如何找出题目中的等量关系?
列分式方程解应用题最关键的步骤是审题,也就是找出题目当中的等量关系,那如何正确地找出等量关系呢?最主要有以下三点:
1.牢记公式,根据公式来找等量关系.例如长方形、正方形的周长和面积公式.
2.熟记数量关系,根据数量关系找等量关系,比如工程问题、行程问题、销售问题、利润问题等等.
1.工程问题
数量关系:工作量=工效×工时
2.行程问题
数量关系:路程=速度×时间
3.销售问题
数量关系:总价=单价×数量
4.利润问题
数量关系:利润=收入-成本
3.抓住关键字词,根据字词的提示找等量关系.
问题3 列分式方程解应用题与列一元一次方程解应用题有何不同?
列分式方程解应用题与列一元一次方程解应用题的步骤大体相同,但是也要注意以下三个问题:
1.列分式方程解应用题的关键是用公式表示一些基本的数量关系;
解:设提速前列车的平均速度为 km/h,
由题意得
方程两边乘 ,得
解得
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
x(x+v)
s(x+v)=x(s+50).
2.列分式方程解应用题一定要验根,先检验方程的解是不是分式方程的解;若是分式方程的解,再检验这个解是否符合题意;
3.列分式方程解应用题要注意题目中的量的单位要统一.
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度
比是3:4,结果甲比乙提前20min到达目的地.求甲乙的速度.
变式练习二
等量关系为:甲所用的时间=乙所用的时间-20分钟
