人教版八年级数学上册13.4课题学习最短路径问题(第一课时)课件 (共22张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.4课题学习最短路径问题(第一课时)课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
八年级—人教版—数学—第十三章
13.4课题学习 最短路径问题(第一课时)
1.能利用轴对称解决简单的最短路径问题.
2.能把实际问题抽象为数学问题,体会图形的变化
在解决最值问题中的作用,感悟转化和类比思想.
学习目标
利用轴对称将最短路径问题转化为“两点之间,线段最短”问题.
学习重点
情境引入
观察图片,生活中你通常如何选择路径,使所走路径最短呢?
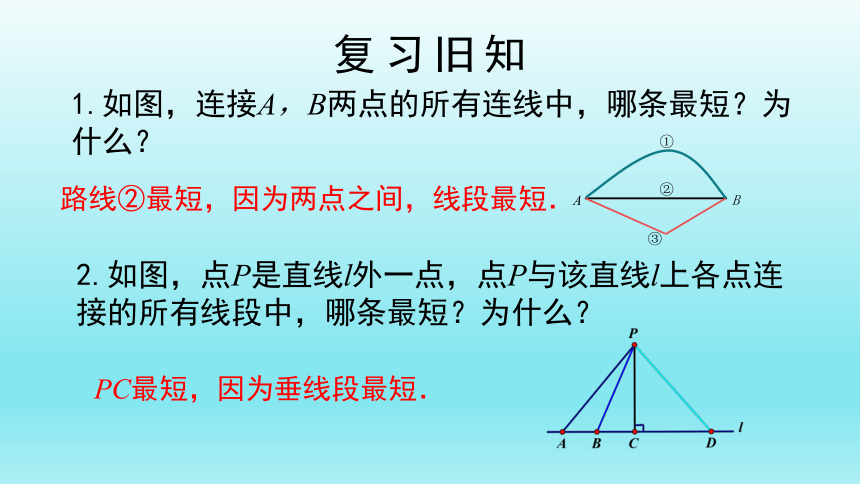
1.如图,连接A,B两点的所有连线中,哪条最短?为什么?
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?
①
②
③
A
B
路线②最短,因为两点之间,线段最短.
PC最短,因为垂线段最短.
复习旧知
例:如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
A
B
l
l
A
B
如图,在直线l上找一点C,使CA+CB最短.
典型问题
l
A
B
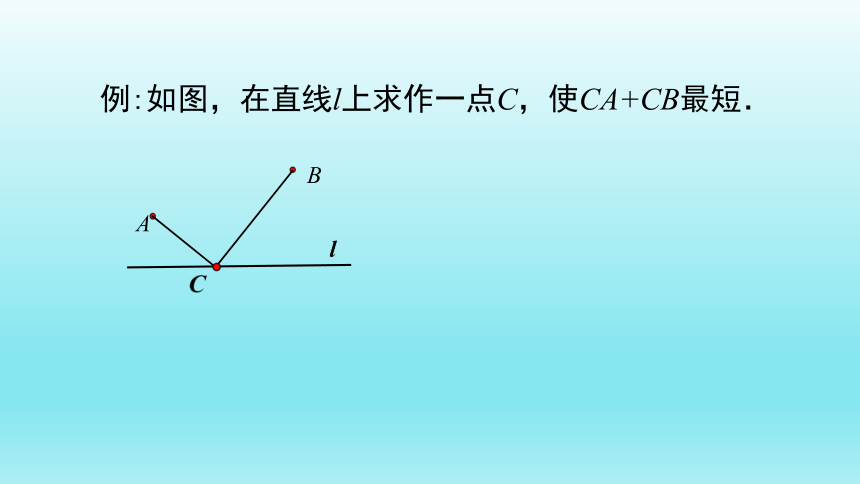
例:如图,在直线l上求作一点C,使CA+CB最短.
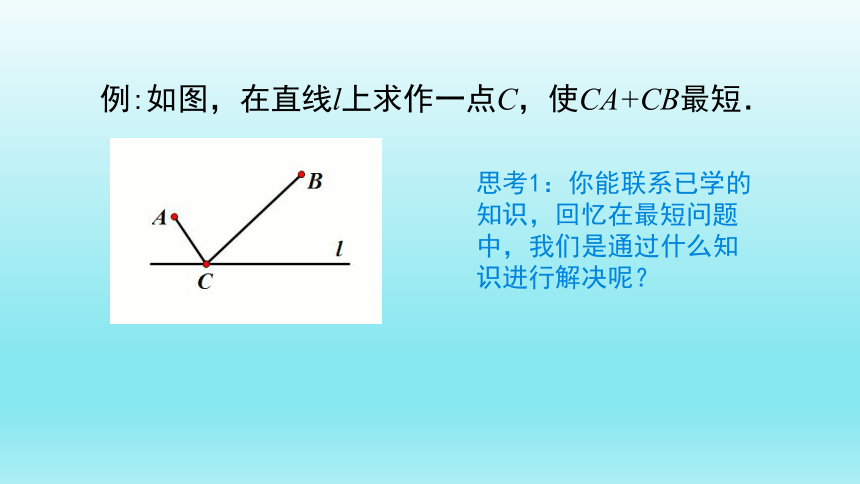
思考1:你能联系已学的知识,回忆在最短问题中,我们是通过什么知识进行解决呢?
例:如图,在直线l上求作一点C,使CA+CB最短.
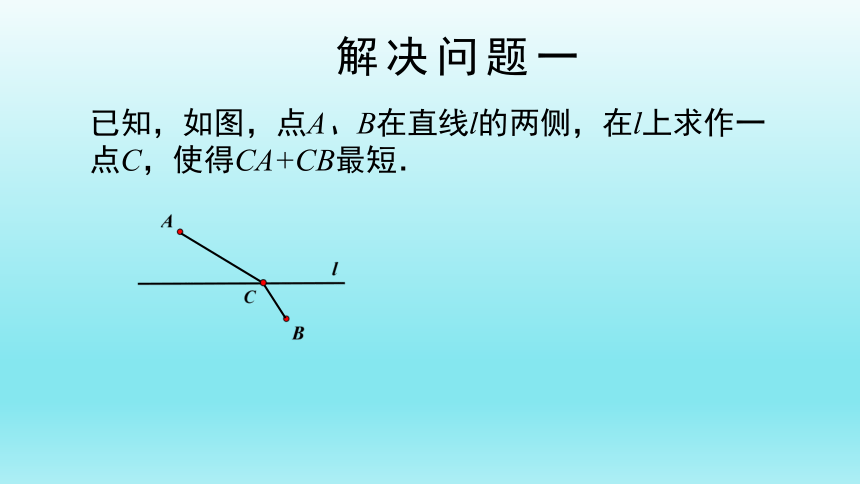
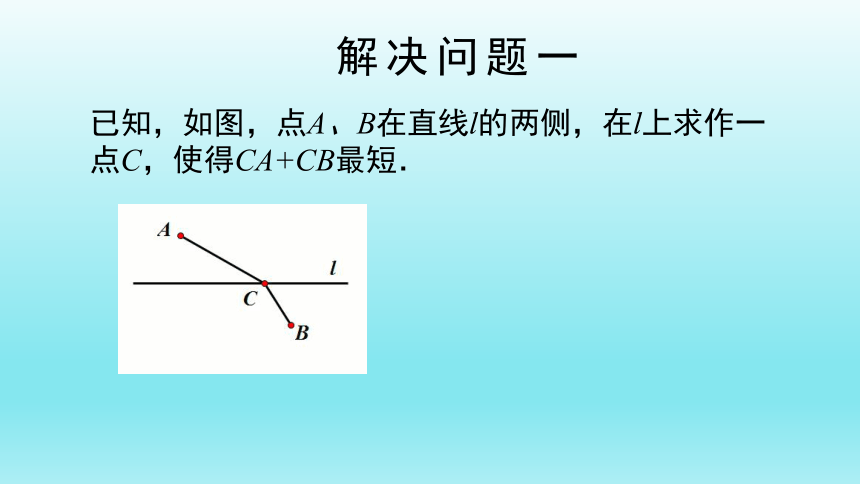
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
连接AB,线段AB与直线l交于点C,点C即为所求.
两点之间,线段最短
作法:
依据:
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
例:如图,在直线l上求作一点C,使CA+CB最短.
思考2:能否通过图形的变换,把左边未知的问题转化为我们右边研究过的问题呢?
l
A
B
A、B在直线l的同侧
A、B在直线l的异侧
解决问题二
l
A
B
问题转化为:
在直线l上求作一点C,使CA+CB'最短.
B'
解决问题二
例:如图,在直线l上求作一点C,使CA+CB最短.
作法:
(1)作点B关于直线l的对称点B',
(2)连接AB'交直线l于点C,
(3)则点C即为所求.
解决问题二
例:如图,在直线l上求作一点C,使CA+CB最短.
在直线上另外任取一点C',连接AC',BC',B'C'.
思考3:如何证明CA+CB最短?
需证明:
证明:
解决问题二
∵
∴
∴
例:如图,在直线l上求作一点C,使CA+CB最短.
方法归纳
A
B
抽象成数学模型
B'
例:如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
l
A
B
联想
旧知
解决实
际问题
用旧知解决新知
思考4:此题,能否作点A关于直线l的对称点呢?
B'
作法:
(1)作点A关于直线l的对称点A',(2)连接A'B交直线l于点C,
(3)则点C即为所求.
如图,牧马人从P地出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到P地.问:这位牧马人怎样走路径最短?
拓展提升
如图,分别在OA、OB上找点C、D,使得PC+CD+DP和最短.
如图,分别在OA、OB上求作点C、D,使得PC+CD+DP和最短.
思考:你能利用解决牧马人饮马问题的办法,解决本题吗?
利用轴对称(实现线段转移).
PC+CD+DP
=
P1C+CD+DP2
两点之间,线段最短.
拓展提升
作法:
(1)过点P分别作关于OA、OB的对称点P1 、P2 ,
(2)连接P1P2分别交OA、OB于点C、D,
(3)点C、D即为所求.
此时PC+CD+DP最短.
拓展提升
如图,分别在OA、OB上求作点C、D,使得PC+CD+DP和最短.
方法归纳
轴对称
解决实际问题
抽象成数学模型
思想方法:类比、转化
如图,牧马人从P地出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到P地.问:这位牧马人怎样走路径最短?
B'
类比、转化
两点之间,线段最短
轴对称变换
轴对称变换
课堂小结
解决方法:利用轴对称实现线段的转移,化折为直.
理论依据:两点之间,线段最短.
思想方法:类比、转化.
最短路径问题:
谢 谢
八年级—人教版—数学—第十三章
13.4课题学习 最短路径问题(第一课时)
1.能利用轴对称解决简单的最短路径问题.
2.能把实际问题抽象为数学问题,体会图形的变化
在解决最值问题中的作用,感悟转化和类比思想.
学习目标
利用轴对称将最短路径问题转化为“两点之间,线段最短”问题.
学习重点
情境引入
观察图片,生活中你通常如何选择路径,使所走路径最短呢?
1.如图,连接A,B两点的所有连线中,哪条最短?为什么?
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?
①
②
③
A
B
路线②最短,因为两点之间,线段最短.
PC最短,因为垂线段最短.
复习旧知
例:如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
A
B
l
l
A
B
如图,在直线l上找一点C,使CA+CB最短.
典型问题
l
A
B
例:如图,在直线l上求作一点C,使CA+CB最短.
思考1:你能联系已学的知识,回忆在最短问题中,我们是通过什么知识进行解决呢?
例:如图,在直线l上求作一点C,使CA+CB最短.
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
连接AB,线段AB与直线l交于点C,点C即为所求.
两点之间,线段最短
作法:
依据:
已知,如图,点A、B在直线l的两侧,在l上求作一点C,使得CA+CB最短.
解决问题一
例:如图,在直线l上求作一点C,使CA+CB最短.
思考2:能否通过图形的变换,把左边未知的问题转化为我们右边研究过的问题呢?
l
A
B
A、B在直线l的同侧
A、B在直线l的异侧
解决问题二
l
A
B
问题转化为:
在直线l上求作一点C,使CA+CB'最短.
B'
解决问题二
例:如图,在直线l上求作一点C,使CA+CB最短.
作法:
(1)作点B关于直线l的对称点B',
(2)连接AB'交直线l于点C,
(3)则点C即为所求.
解决问题二
例:如图,在直线l上求作一点C,使CA+CB最短.
在直线上另外任取一点C',连接AC',BC',B'C'.
思考3:如何证明CA+CB最短?
需证明:
证明:
解决问题二
∵
∴
∴
例:如图,在直线l上求作一点C,使CA+CB最短.
方法归纳
A
B
抽象成数学模型
B'
例:如图,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
l
A
B
联想
旧知
解决实
际问题
用旧知解决新知
思考4:此题,能否作点A关于直线l的对称点呢?
B'
作法:
(1)作点A关于直线l的对称点A',(2)连接A'B交直线l于点C,
(3)则点C即为所求.
如图,牧马人从P地出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到P地.问:这位牧马人怎样走路径最短?
拓展提升
如图,分别在OA、OB上找点C、D,使得PC+CD+DP和最短.
如图,分别在OA、OB上求作点C、D,使得PC+CD+DP和最短.
思考:你能利用解决牧马人饮马问题的办法,解决本题吗?
利用轴对称(实现线段转移).
PC+CD+DP
=
P1C+CD+DP2
两点之间,线段最短.
拓展提升
作法:
(1)过点P分别作关于OA、OB的对称点P1 、P2 ,
(2)连接P1P2分别交OA、OB于点C、D,
(3)点C、D即为所求.
此时PC+CD+DP最短.
拓展提升
如图,分别在OA、OB上求作点C、D,使得PC+CD+DP和最短.
方法归纳
轴对称
解决实际问题
抽象成数学模型
思想方法:类比、转化
如图,牧马人从P地出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到P地.问:这位牧马人怎样走路径最短?
B'
类比、转化
两点之间,线段最短
轴对称变换
轴对称变换
课堂小结
解决方法:利用轴对称实现线段的转移,化折为直.
理论依据:两点之间,线段最短.
思想方法:类比、转化.
最短路径问题:
谢 谢
