人教版八年级数学上册 13.2画轴对称图形(第二课时)课件 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册 13.2画轴对称图形(第二课时)课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
八年级—人教版—数学—第十三章
13.2 画轴对称图形(第二课时)
学习目标:
1.探究在平面直角坐标系中关于x轴和y轴的对称点的坐标特点.
2.能在平面直角坐标系中画出简单的关于x轴和y轴的对称图形.
3.能运用坐标系中的轴对称特点解决简单的问题.
学习重点:
理解图形上点的坐标变化与图形的轴对称变换之间的关系并能灵活运用坐标系中的轴对称特点解决简单的问题.
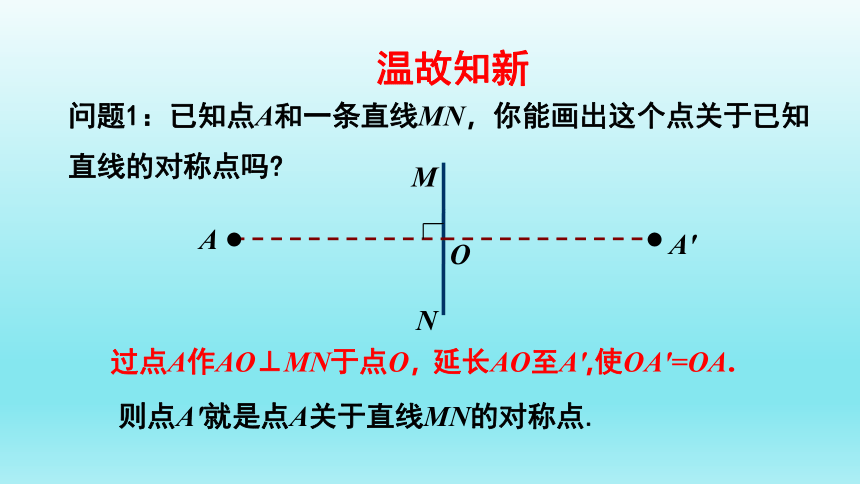
问题1:已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A′
M
N
则点A′就是点A关于直线MN的对称点.
O
延长AO至A′,使OA′=OA.
过点A作AO⊥MN于点O,
温故知新
思考:
平面直角坐标系是数形结合的一个桥梁,如果我们在平面直角坐标系中作轴对称图形,能不能从数量的角度刻画轴对称呢?
探究思考
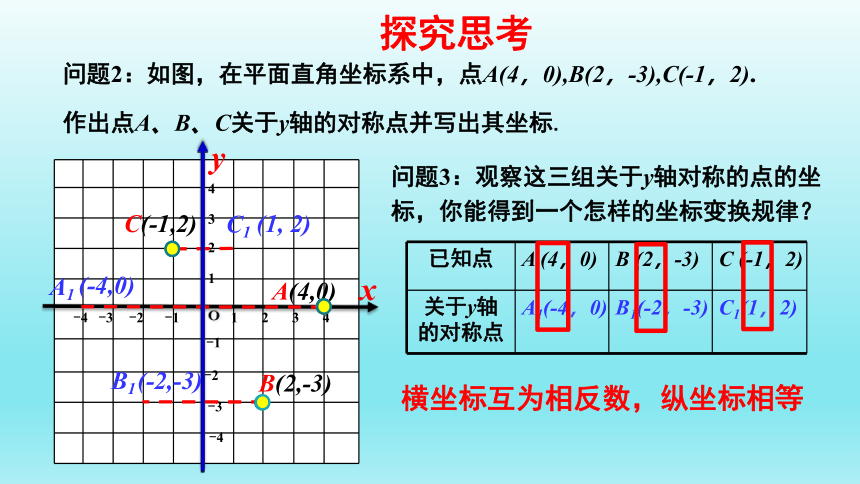
问题2:如图,在平面直角坐标系中,点A(4,0),B(2,-3),C(-1,2).
作出点A、B、C关于y轴的对称点并写出其坐标.
1
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
O
A(4,0)
B(2,-3)
C(-1,2)
A1
B1
C1
已知点 A (4,0) B (2,-3) C (-1,2)
关于y轴的对称点 A1(-4,0) B1(-2,-3) C1(1,2)
问题3:观察这三组关于y轴对称的点的坐标,你能得到一个怎样的坐标变换规律?
横坐标互为相反数,纵坐标相等
(1, 2)
(-4,0)
(-2,-3)
b
a
-a
x
y
O
P(a,b)
P1
探究思考
( ,b)
-a
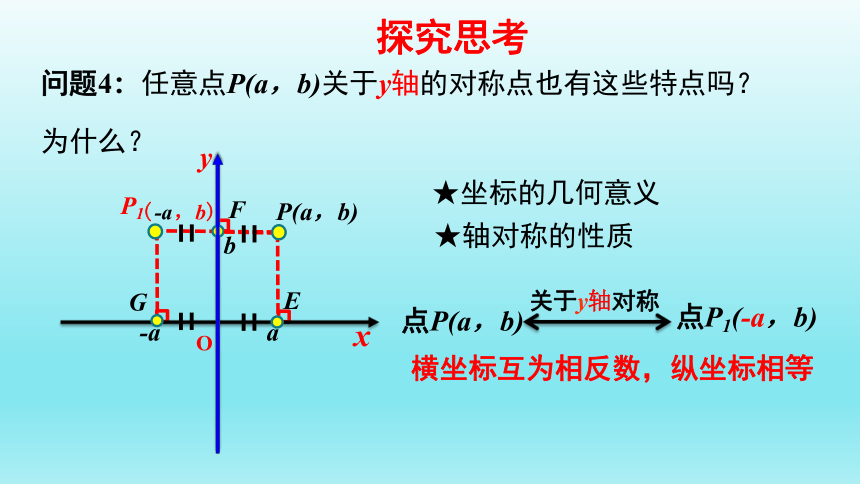
问题4:任意点P(a,b)关于y轴的对称点也有这些特点吗?
为什么?
点P1(-a,b)
点P(a,b)
关于y轴对称
横坐标互为相反数,纵坐标相等
E
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习1:
1.点P(-2.5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
(2.5 , 6 )
2
-5
(x , y)
( , )
-x
y
(2.5 , )
点P2(a,-b)
关于x轴对称
点P(a,b)
探究思考
点P1(-a,b)
点P(a,b)
关于y轴对称
问题5:关于y轴对称的点的坐标是有规律的,那么关于x轴对称的点的坐标是不是也有规律呢?如果有,你能猜想一下坐标变换的规律吗?
横坐标相等,纵坐标互为相反数
横坐标互为相反数,纵坐标相等
a
E
b
x
y
O
P(a,b)
P2
探究思考
(a, )
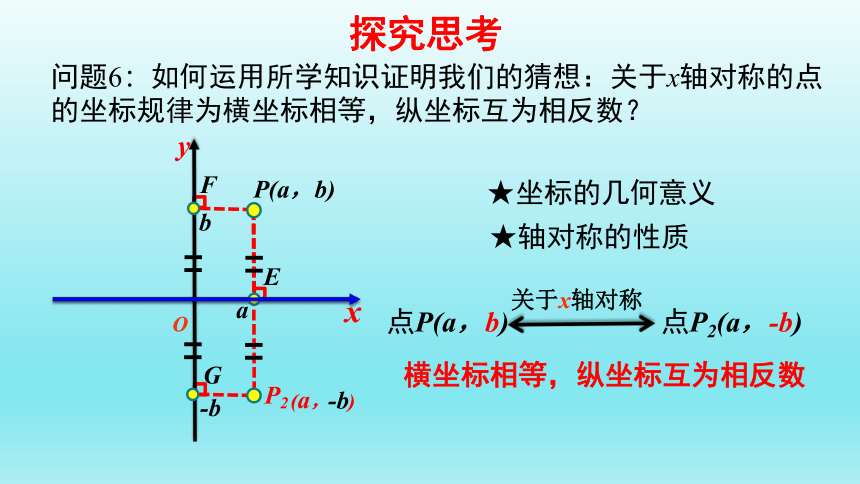
问题6:如何运用所学知识证明我们的猜想:关于x轴对称的点的坐标规律为横坐标相等,纵坐标互为相反数?
点P2(a,-b)
关于x轴对称
点P(a,b)
-b
-b
横坐标相等,纵坐标互为相反数
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习2:
1.点P(-2.5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,b =_____.
(- 2.5 , -6 )
-2
5
(x , y)
( , )
x
-y
(- 2.5 , )
P2(-x,y)
●
P(x,y)
●
y
x
O
P1(x,-y)
●
知识归纳
点(x, y)关于x 轴对称的点的坐标为(x,-y)
关于坐标轴对称的点的坐标规律:
点关于直线对称的几何特点用坐标的代数形式来表现出来,体现了我们数学中的数形结合思想方法.
点(x, y)关于y 轴对称的点的坐标为 (-x,y)
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
典型例题
解:(1)点(x,y)关于y 轴对称的点的坐标为
(-x,y)因此四边形ABCD 的顶点A,B,C,D
关于y 轴对称的点坐标分别为:
A1( , ), B1( , ),
C1( , ), D1( , ),
5 1
2 1
2 5
5 4
依次连接A2B2,B2C2, C2D2, A2D2 ,
A2
(2)点(x,y)关于x 轴对称的点的坐标为
(x,-y),因此四边形ABCD 的顶点A,B,
C,D 关于x 轴对称的点分别为:
A2( , ),B2( , ),
C2( , ),D2( , ),
-2 -5
-5 -1
-2 -1
-5 -4
D2
C2
B2
典型例题
则四边形A2B2C2D2为所求图形.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
依次连接A2B2,B2C2, C2D2, A2D2
A2
(2)作四边形ABCD 的顶点A,B,C,D 关于
x 轴对称的点分别为A2、B2、 C2、 D2,
D2
C2
B2
典型例题
则四边形A2B2C2D2为所求图形.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
(2)四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2(-5,-1),B2(-2,-1),
C2(-2,-5), D2(-5,-4)
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
(2)作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
在坐标系中作已知图形关于坐标轴对称图形
精准
快捷
适用范围广
1.找对称点坐标
2.描点
3.连线
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x轴的对称点在第一象限,求a的取值范围.
解:(1)依题意得
∵点P、A关于y轴对称,
解决给定两个含参坐标的轴对称题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
横坐标互为相反数,纵坐标相等
∴
∴
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)∵P关于x轴对称点的坐标P′(a+1,-2a+1)
P′(a+1,-2a+1)
又∵P关于x轴对称点P′在第一象限
解得
即a的取值范围是
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)依题意得:P点在第四象限,
x
y
O
P′
P
一般先写出对称点的坐标或判断已知点所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
即a的取值范围是
解得
P2(-x,y)
●
二、在平面直角系中作轴对称图形:
P(x,y)
●
y
x
O
P1(x,-y)
●
课堂总结
找对称点坐标 描点 连线
(x , y)
( , )
x
-y
关于x轴对称
(x , y)
( , )
-x
y
关于y轴对称
把图形的对称问题转化为关键点的对称问题
一、关于坐标轴对称的点的坐标规律:
谢 谢
八年级—人教版—数学—第十三章
13.2 画轴对称图形(第二课时)
学习目标:
1.探究在平面直角坐标系中关于x轴和y轴的对称点的坐标特点.
2.能在平面直角坐标系中画出简单的关于x轴和y轴的对称图形.
3.能运用坐标系中的轴对称特点解决简单的问题.
学习重点:
理解图形上点的坐标变化与图形的轴对称变换之间的关系并能灵活运用坐标系中的轴对称特点解决简单的问题.
问题1:已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A′
M
N
则点A′就是点A关于直线MN的对称点.
O
延长AO至A′,使OA′=OA.
过点A作AO⊥MN于点O,
温故知新
思考:
平面直角坐标系是数形结合的一个桥梁,如果我们在平面直角坐标系中作轴对称图形,能不能从数量的角度刻画轴对称呢?
探究思考
问题2:如图,在平面直角坐标系中,点A(4,0),B(2,-3),C(-1,2).
作出点A、B、C关于y轴的对称点并写出其坐标.
1
x
y
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
O
A(4,0)
B(2,-3)
C(-1,2)
A1
B1
C1
已知点 A (4,0) B (2,-3) C (-1,2)
关于y轴的对称点 A1(-4,0) B1(-2,-3) C1(1,2)
问题3:观察这三组关于y轴对称的点的坐标,你能得到一个怎样的坐标变换规律?
横坐标互为相反数,纵坐标相等
(1, 2)
(-4,0)
(-2,-3)
b
a
-a
x
y
O
P(a,b)
P1
探究思考
( ,b)
-a
问题4:任意点P(a,b)关于y轴的对称点也有这些特点吗?
为什么?
点P1(-a,b)
点P(a,b)
关于y轴对称
横坐标互为相反数,纵坐标相等
E
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习1:
1.点P(-2.5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
(2.5 , 6 )
2
-5
(x , y)
( , )
-x
y
(2.5 , )
点P2(a,-b)
关于x轴对称
点P(a,b)
探究思考
点P1(-a,b)
点P(a,b)
关于y轴对称
问题5:关于y轴对称的点的坐标是有规律的,那么关于x轴对称的点的坐标是不是也有规律呢?如果有,你能猜想一下坐标变换的规律吗?
横坐标相等,纵坐标互为相反数
横坐标互为相反数,纵坐标相等
a
E
b
x
y
O
P(a,b)
P2
探究思考
(a, )
问题6:如何运用所学知识证明我们的猜想:关于x轴对称的点的坐标规律为横坐标相等,纵坐标互为相反数?
点P2(a,-b)
关于x轴对称
点P(a,b)
-b
-b
横坐标相等,纵坐标互为相反数
F
G
★坐标的几何意义
★轴对称的性质
知识归纳
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习2:
1.点P(-2.5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,b =_____.
(- 2.5 , -6 )
-2
5
(x , y)
( , )
x
-y
(- 2.5 , )
P2(-x,y)
●
P(x,y)
●
y
x
O
P1(x,-y)
●
知识归纳
点(x, y)关于x 轴对称的点的坐标为(x,-y)
关于坐标轴对称的点的坐标规律:
点关于直线对称的几何特点用坐标的代数形式来表现出来,体现了我们数学中的数形结合思想方法.
点(x, y)关于y 轴对称的点的坐标为 (-x,y)
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
典型例题
解:(1)点(x,y)关于y 轴对称的点的坐标为
(-x,y)因此四边形ABCD 的顶点A,B,C,D
关于y 轴对称的点坐标分别为:
A1( , ), B1( , ),
C1( , ), D1( , ),
5 1
2 1
2 5
5 4
依次连接A2B2,B2C2, C2D2, A2D2 ,
A2
(2)点(x,y)关于x 轴对称的点的坐标为
(x,-y),因此四边形ABCD 的顶点A,B,
C,D 关于x 轴对称的点分别为:
A2( , ),B2( , ),
C2( , ),D2( , ),
-2 -5
-5 -1
-2 -1
-5 -4
D2
C2
B2
典型例题
则四边形A2B2C2D2为所求图形.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
依次连接A2B2,B2C2, C2D2, A2D2
A2
(2)作四边形ABCD 的顶点A,B,C,D 关于
x 轴对称的点分别为A2、B2、 C2、 D2,
D2
C2
B2
典型例题
则四边形A2B2C2D2为所求图形.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4).
(1)若四边形A1B1C1D1与四边形ABCD关于y轴成轴对称,请写出四边形A1B1C1D1
顶点坐标.
(2)作出四边形ABCD关于x轴的轴对称图形.
(2)四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A2(-5,-1),B2(-2,-1),
C2(-2,-5), D2(-5,-4)
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
(2)作四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为A2、B2、 C2、 D2,
依次连接A2B2,B2C2, C2D2, A2D2
则四边形A2B2C2D2为所求图形.
在坐标系中作已知图形关于坐标轴对称图形
精准
快捷
适用范围广
1.找对称点坐标
2.描点
3.连线
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x轴的对称点在第一象限,求a的取值范围.
解:(1)依题意得
∵点P、A关于y轴对称,
解决给定两个含参坐标的轴对称题可根据关于x轴、y轴对称的点的特征列方程(组)求解.
横坐标互为相反数,纵坐标相等
∴
∴
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)∵P关于x轴对称点的坐标P′(a+1,-2a+1)
P′(a+1,-2a+1)
又∵P关于x轴对称点P′在第一象限
解得
即a的取值范围是
例2.已知点P的坐标为P(a+1,2a-1)
(1)若点P与点A (2a-b,5+a)关于y轴对称,求a、b的值;
(2)若点P关于x 轴的对称点P′在第一象限,求a的取值范围.
解:(2)依题意得:P点在第四象限,
x
y
O
P′
P
一般先写出对称点的坐标或判断已知点所在的象限,再由各象限内点的坐标的符号,列不等式(组)求解.
即a的取值范围是
解得
P2(-x,y)
●
二、在平面直角系中作轴对称图形:
P(x,y)
●
y
x
O
P1(x,-y)
●
课堂总结
找对称点坐标 描点 连线
(x , y)
( , )
x
-y
关于x轴对称
(x , y)
( , )
-x
y
关于y轴对称
把图形的对称问题转化为关键点的对称问题
一、关于坐标轴对称的点的坐标规律:
谢 谢
