人教版八年级数学上册13.1.1轴对称课件 (共21张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1.1轴对称课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 07:54:53 | ||
图片预览





文档简介
(共21张PPT)
八年级—人教版—数学—第十三章
13.1.1 轴对称
学习目标:
1.通过具体实例了解轴对称图形、图形的轴对称的概念.
2.探索两个图形成轴对称的性质和轴对称图形的性质,学会用符号语言去描述这些性质.
3.理解线段垂直平分线的概念.
4.认识并欣赏自然界和现实生活中的轴对称图形.
学习重点:
轴对称的概念与性质.
课前准备:
正方形纸片、剪刀.
一、引出新知
二、探究新知
【问题1】如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
(一)轴对称图形
l
轴对称图形
对称轴
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
这时,我们也说这个图形关于这条直线
(成轴)对称.
思考:你能举出一些轴对称图形的例子吗?
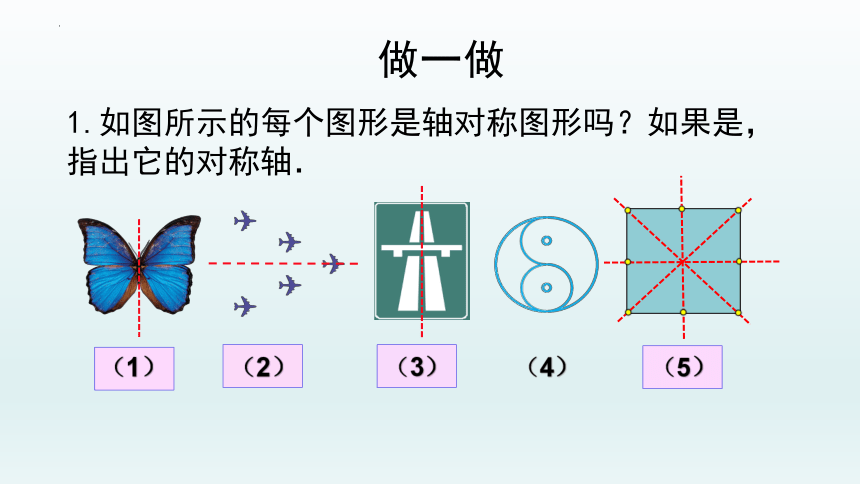
(1) (2) (3) (4) (5)
做一做
1.如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
二、探究新知
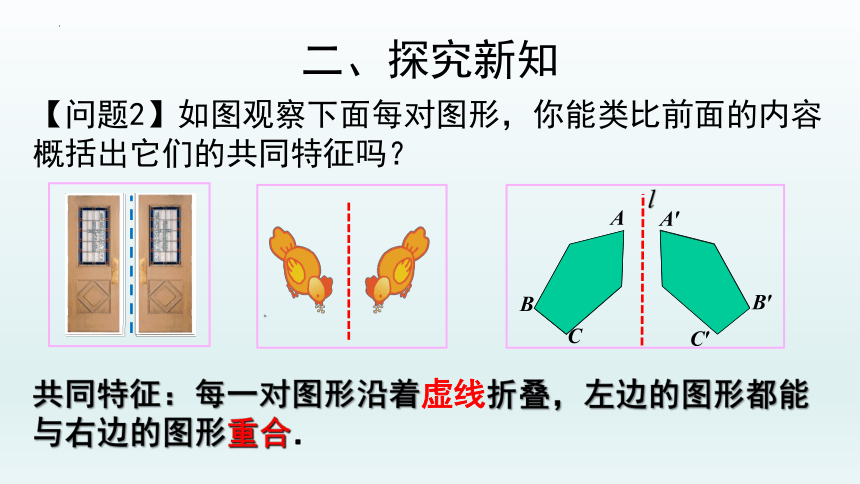
共同特征:每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
B
A′
A
C
B′
C′
【问题2】如图观察下面每对图形,你能类比前面的内容概括出它们的共同特征吗?
l
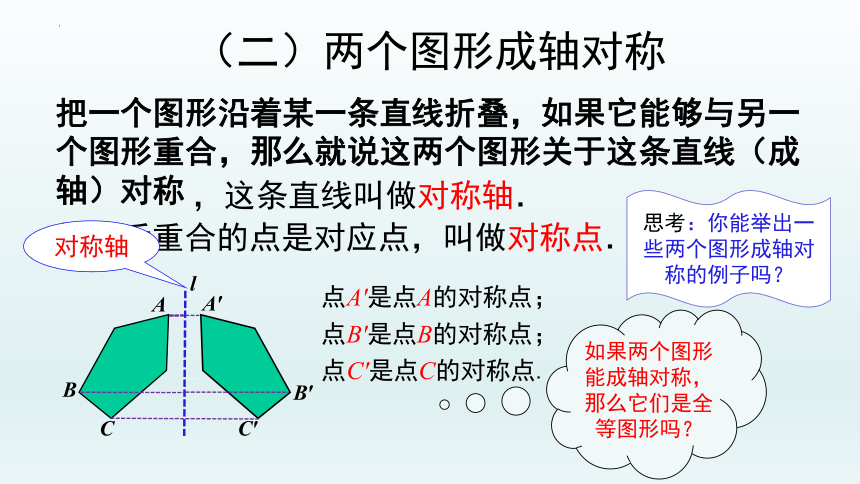
(二)两个图形成轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称
如果两个图形能成轴对称,那么它们是全等图形吗?
B
A′
A
C
B′
C′
思考:你能举出一些两个图形成轴对称的例子吗?
,这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
l
点A'是点A的对称点;
点B'是点B的对称点;
点C'是点C的对称点.
对称轴
B
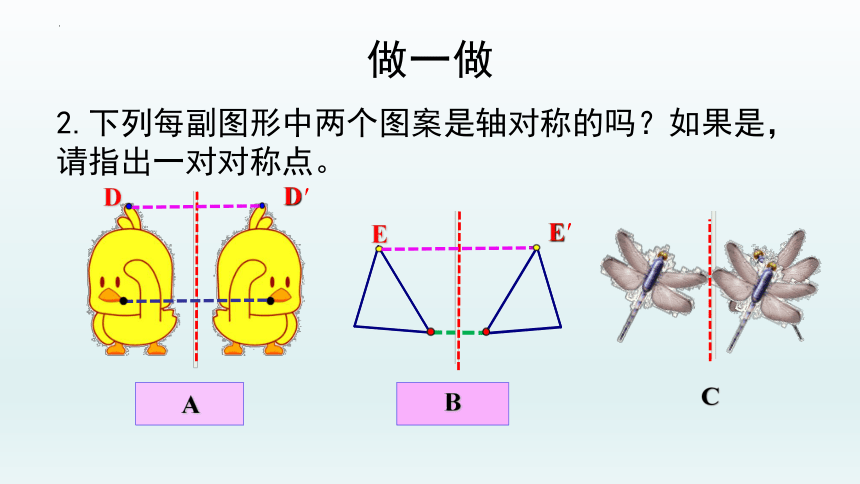
做一做
2.下列每副图形中两个图案是轴对称的吗?如果是,请指出一对对称点。
C
A
D
E
D′
E′
思考
你能说明轴对称图形和两个图形成轴对称有什么区别与联系吗?
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个全等图形的对称关系
1.都能沿着某条直线折叠后重合.
2.把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
二、探究新知
【问题3】如图,△ABC 和△A′B′C′关于直线MN 对称,点A′,B′,C′分别是点A,B,C 的对称点,则图中线段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
N
M
二、探究新知
如图所示: 点A与点A′是对称点,
设AA′交对称轴MN于点P,将△ABC或△A′B′C′
沿MN折叠后,点A与点A′重合.
则有 AP=PA′,∠MPA=∠MPA′=90°
同理 BP1=P1B′,BB′⊥MN,
C′
发现:对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
P1
P2
A′
即 AA′⊥MN
P
B'
CP2=P2C′,CC′⊥MN.
(三)线段垂直平分线的概念
线段垂直平分线的概念:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
符号语言表示为:
若MN⊥AA′,垂足为P, 且 AP=A′P,则称直线MN是线段AA ′的垂直平分线.
我们也把这条直线叫做中垂线.
(四)两个图形成轴对称的性质
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
思考:如果将其中的“三角形”改为“四边形”“五边形”…其他条件不变,前面的结论还成立吗?
l
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.(即对称点所连线段被对称轴垂直平分;对称轴垂直平分对称点所连线段.)
(五)轴对称图形的性质
【问题4】下图是一个轴对称图形,你能发现什么结论?能说明理由吗?
结论:
直线l垂直线段AA′、BB′,
直线l平分线段 AA′、BB′,
(或直线l是线段AA ′,BB′的垂直平分线.)
l
(五)轴对称图形的性质
轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
符号语言表示为:
∵直线l为正五边形的对称轴,
∴直线l垂直平分BB′与AA′.
3.如图,在四边形ABCD中,AC是对称轴,点B与点D是对称点,AB=3,∠ACB=30°,则AD= ,∠ACD= ,AC与BD的位置关系是 。
做一做
3
30°
互相垂直
AC是对称轴
点B与点D是对称点
四边形ABCD是轴对称图形
AC垂直平分BD
3
30°
3
30°
分析:
ABC ADC
课堂小结
本节课知识点对应数学课本P58-60
轴对称
重要内容
线段的垂直平分线
两个图形成轴对称
轴对称图形
性质
概念
性质
概念
区别与联系
课后作业
完成课本P64-65习题13.1第1、2、3、4、5题.
谢 谢 !
八年级—人教版—数学—第十三章
13.1.1 轴对称
学习目标:
1.通过具体实例了解轴对称图形、图形的轴对称的概念.
2.探索两个图形成轴对称的性质和轴对称图形的性质,学会用符号语言去描述这些性质.
3.理解线段垂直平分线的概念.
4.认识并欣赏自然界和现实生活中的轴对称图形.
学习重点:
轴对称的概念与性质.
课前准备:
正方形纸片、剪刀.
一、引出新知
二、探究新知
【问题1】如图,把一张纸对折,剪出一个图案(折痕处不要完全剪断),再打开这张对折的纸,就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
(一)轴对称图形
l
轴对称图形
对称轴
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
这时,我们也说这个图形关于这条直线
(成轴)对称.
思考:你能举出一些轴对称图形的例子吗?
(1) (2) (3) (4) (5)
做一做
1.如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
二、探究新知
共同特征:每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
B
A′
A
C
B′
C′
【问题2】如图观察下面每对图形,你能类比前面的内容概括出它们的共同特征吗?
l
(二)两个图形成轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称
如果两个图形能成轴对称,那么它们是全等图形吗?
B
A′
A
C
B′
C′
思考:你能举出一些两个图形成轴对称的例子吗?
,这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
l
点A'是点A的对称点;
点B'是点B的对称点;
点C'是点C的对称点.
对称轴
B
做一做
2.下列每副图形中两个图案是轴对称的吗?如果是,请指出一对对称点。
C
A
D
E
D′
E′
思考
你能说明轴对称图形和两个图形成轴对称有什么区别与联系吗?
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 一个图形具有的特殊形状
两个全等图形的对称关系
1.都能沿着某条直线折叠后重合.
2.把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称.
二、探究新知
【问题3】如图,△ABC 和△A′B′C′关于直线MN 对称,点A′,B′,C′分别是点A,B,C 的对称点,则图中线段AA′,BB′,CC′与直线MN 有什么关系?
A
B
C
N
M
二、探究新知
如图所示: 点A与点A′是对称点,
设AA′交对称轴MN于点P,将△ABC或△A′B′C′
沿MN折叠后,点A与点A′重合.
则有 AP=PA′,∠MPA=∠MPA′=90°
同理 BP1=P1B′,BB′⊥MN,
C′
发现:对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.
P1
P2
A′
即 AA′⊥MN
P
B'
CP2=P2C′,CC′⊥MN.
(三)线段垂直平分线的概念
线段垂直平分线的概念:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
符号语言表示为:
若MN⊥AA′,垂足为P, 且 AP=A′P,则称直线MN是线段AA ′的垂直平分线.
我们也把这条直线叫做中垂线.
(四)两个图形成轴对称的性质
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
思考:如果将其中的“三角形”改为“四边形”“五边形”…其他条件不变,前面的结论还成立吗?
l
性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.(即对称点所连线段被对称轴垂直平分;对称轴垂直平分对称点所连线段.)
(五)轴对称图形的性质
【问题4】下图是一个轴对称图形,你能发现什么结论?能说明理由吗?
结论:
直线l垂直线段AA′、BB′,
直线l平分线段 AA′、BB′,
(或直线l是线段AA ′,BB′的垂直平分线.)
l
(五)轴对称图形的性质
轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
符号语言表示为:
∵直线l为正五边形的对称轴,
∴直线l垂直平分BB′与AA′.
3.如图,在四边形ABCD中,AC是对称轴,点B与点D是对称点,AB=3,∠ACB=30°,则AD= ,∠ACD= ,AC与BD的位置关系是 。
做一做
3
30°
互相垂直
AC是对称轴
点B与点D是对称点
四边形ABCD是轴对称图形
AC垂直平分BD
3
30°
3
30°
分析:
ABC ADC
课堂小结
本节课知识点对应数学课本P58-60
轴对称
重要内容
线段的垂直平分线
两个图形成轴对称
轴对称图形
性质
概念
性质
概念
区别与联系
课后作业
完成课本P64-65习题13.1第1、2、3、4、5题.
谢 谢 !
