中考考前数学压轴题预测(压轴题+详解)
文档属性
| 名称 | 中考考前数学压轴题预测(压轴题+详解) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-10 00:00:00 | ||
图片预览




文档简介
中考考前压轴题预测
【预测题】1、已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°,动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
(1)求直线AC的解析式;
(2)试求出当t为何值时,△OAC与△PAQ相似;
(3)若⊙P的半径为,⊙Q的半径为;当⊙P与对角线AC相切时,判断⊙Q与直线AC、BC的位置关系,并求出Q点坐标。
解:(1)
(2)①当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,①若∠APQ=90°,则△APQ∽△OCA,
∵t>2.5,∴符合条件.
②若∠AQP=90°,则△APQ∽△∠OAC,
∵t>2.5,∴符合条件.
综上可知,当时,△OAC与△APQ相似.
(3)⊙Q与直线AC、BC均相切,Q点坐标为()。
【预测题】2、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
解:(1);.(2)在中,,
.
设点的坐标为,其中,顶点,
∴设抛物线解析式为.
①如图①,当时,,.
解得(舍去);...解得.
抛物线的解析式为
②如图②,当时,,.
解得(舍去).
③当时,,这种情况不存在.
综上所述,符合条件的抛物线解析式是.
(3)存在点,使得四边形的周长最小.
如图③,作点关于轴的对称点,作点关于
轴的对称点,连接,分别与轴、轴交于
点,则点就是所求点.
,.
..又,,此时四边形的周长最小值是.
【预测题】3、如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.
(1)①试判断BG与2BP的大小关系,并说明理由;
②用x的代数式表示线段DG的长,并写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式,并求出S的最大值;
(3)以P、E、F为顶点的三角形与△EDG是否可能相似?如果能相似,请求出BP的长,如果不能,请说明理由。
解:(1)①在等边三角形ABC中,∠B=60°,∵PG⊥AB,
∴∠BGP=30°,∴BG=2BP.
②∵PF//AC,∴△PBF为等边三角形,∴BF=PF=PB=x.
又∵BG=2x,BD=1,∴DG=2x-1,∴0<2x-1≤1,∴.
(2)S=DE×DF=
=
当时,.
(3)①如图1,若∠PFE=Rt∠,则两三角形相似,
此时可得DF=DG
即
解得:.
②如图2,若∠PEF=Rt∠,则两三角形相似,
此时可得DF=EF=BP,
即.解得:.
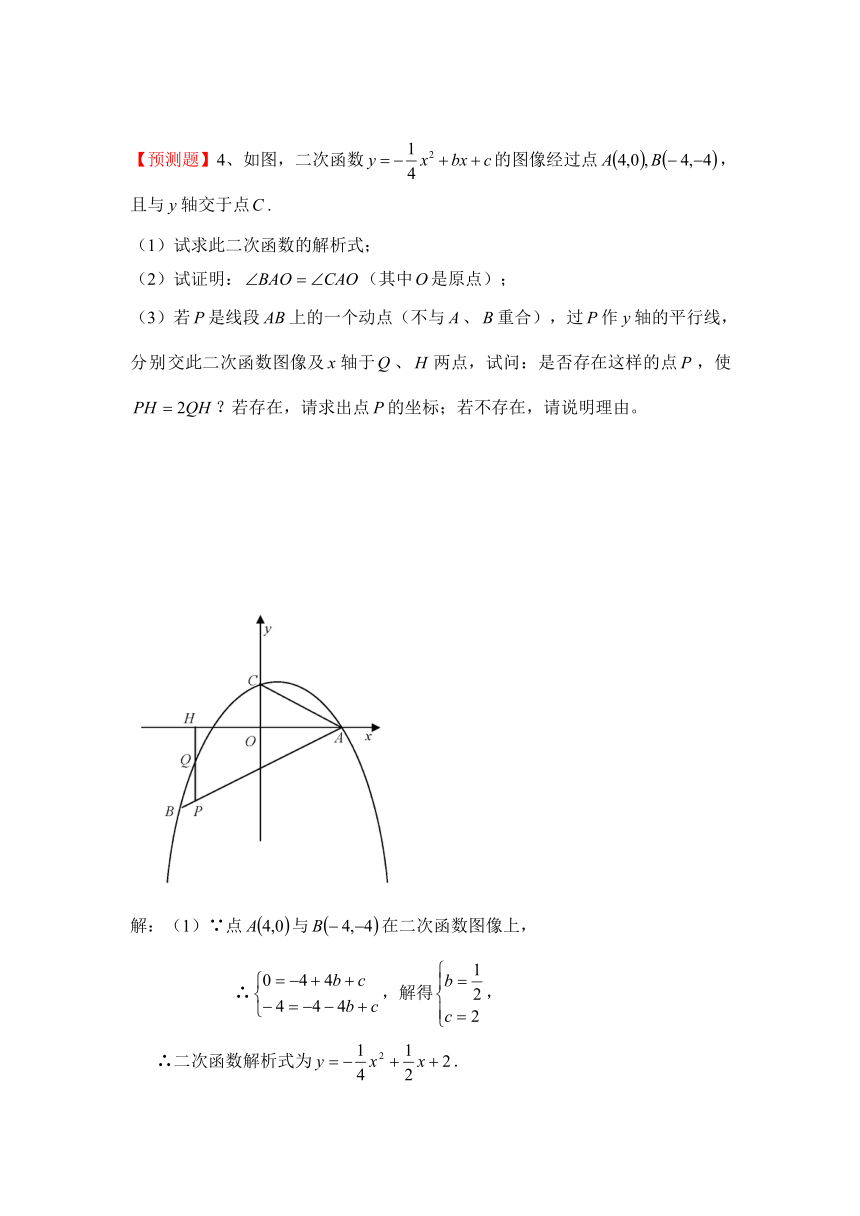
【预测题】4、如图,二次函数的图像经过点,
且与轴交于点.
(1)试求此二次函数的解析式;
(2)试证明:(其中是原点);
(3)若是线段上的一个动点(不与、重合),过作轴的平行线,分别交此二次函数图像及轴于、两点,试问:是否存在这样的点,使?若存在,请求出点的坐标;若不存在,请说明理由。
解:(1)∵点与在二次函数图像上,
∴,解得,
∴二次函数解析式为.
(2)过作轴于点,由(1)得,则在中,,又在中,,
∵,∴.
(3)由与,可得直线的解析式为,
设,则,
∴.∴.
当,解得 (舍去),∴.
当,解得 (舍去),∴.
综上所述,存在满足条件的点,它们是与.
【预测题】5、如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6=,过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
解:(1)∵,CD=3,CQ=x,∴.
图象如图所示.
(2)方法一:,CP=8k-xk,CQ=x,
∴.∵抛物线顶点坐标是(4,12),
∴.解得.则点P的速度每秒厘米,AC=12厘米.
方法二:观察图象知,当x=4时,△PCQ面积为12.
此时PC=AC-AP=8k-4k=4k,CQ=4.∴由,得 .
解得.则点P的速度每秒厘米,AC=12厘米.
方法三:设y2的图象所在抛物线的解析式是.
∵图象过(0,0),(4,12),(8,0),
∴ 解得 ∴. ①
∵,CP=8k-xk,CQ=x,∴. ②
比较①②得.则点P的速度每秒厘米,AC=12厘米.
(3)①观察图象,知线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积).②由⑵得 .(方法二,)
∵EF=y2-y1,∴EF=,
∵二次项系数小于0,∴在范围,当时,最大.
【预测题】6、如图,在中,,、分别是边、
上的两个动点(不与、重合),且保持,以为边,在点的异侧作正方形.
(1)试求的面积;
(2)当边与重合时,求正方形的边长;
(3)设,与正方形重叠部分的面积为,试求关于的函数关系式,并写出定义域;
(4)当是等腰三角形时,请直接写出的长。
解:(1)过作于,∵,∴.
则在中,,∴.
(2)令此时正方形的边长为,则,解得.
(3)当时,.
当时,.
(4).
【预测题】7、如图已知点A (-2,4) 和点B (1,0)都在抛物线上.
(1)求、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′ 的交点为点C,试在轴上找点D,使得以点B′、C、D为顶点的三角形与相似.
解:(1)根据题意,得: 解得
(2)四边形A A′B′B为菱形,则A A′=B′B= AB=5
∵
=
∴ 向右平移5个单位的抛物线解析式为
(3)设D(x,0)根据题意,得:AB=5,
∵∠A=∠B B′A
ⅰ) △ABC∽△B′CD时,∠ABC=∠B′CD ,∴BD=6-x, 由 得 解得x=3, ∴D(3,0)
ⅱ)△ABC∽△B′DC时,
∴ 解得 ∴
【预测题】8、如 图,已知直角梯形ABCD中,AD∥BC,A B⊥BC ,AD=2,AB=8,
CD=10.
(1)求梯形ABCD的面积S;
(2)动点P从点B出发,以1cm/s的速度、沿B→A→D→C方向,向点C运动;动点Q从点C出发,以1cm/s的速度、沿C→D→A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由;
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
解:
在Rt△DCH中,
(2)①
经计算,PQ不平分梯形ABCD的面积
②
,-
【预测题】9、如图,⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(,0),CAB=90°,AC=AB,顶点A在⊙O上运动.
(1)当点A在x轴上时,求点C的坐标;
(2)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(3)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;
(4)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
解:(1)当点A的坐标为(1,0)时,AB=AC=-1,点C的坐标为(1,-1);
当点A的坐标为(-1,0)时,AB=AC=+1,点C的坐标为(-1,+1);
(2)直线BC与⊙O相切,过点O作OM⊥BC于点M,∴∠OBM=∠BOM=45°,
∴OM=OB·sin45°=1,∴直线BC与⊙O相切
(3)过点A作AE⊥OB于点E
在Rt△OAE中,AE2=OA2-OE2=1-x2,
在Rt△BAE中,AB2=AE2+BE2=(1-x2) +(-x)2=3-2x
∴S=AB·AC= AB2=(3-2x)=
其中-1≤x≤1,
当x=-1时,S的最大值为,
当x=1时,S的最小值为.
(4)①当点A位于第一象限时(如右图):
连接OA,并过点A作AE⊥OB于点E
∵直线AB与⊙O相切,∴∠OAB=90°,
又∵∠CAB=90°,∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线上,∴∠AOB=∠C=45°,
在Rt△OAE中,OE=AE=.点A的坐标为(,)
过A、B两点的直线为y=-x+.
②当点A位于第四象限时(如右图)
点A的坐标为(,-),过A、B两点的直线为y=x-.
【预测题】10、已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上,∴c=8,将A(-6,0)、B(2,0)代入表达式,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)依题意,AE=m,则BE=8-m,∵OA=6,OC=8,∴AC=10
∵EF∥AC ∴△BEF∽△BAC,∴= 即=,∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(4)存在.
理由:∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8 ∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.
【预测题】11、数学课上,张老师出示了问题1:如图25-1,四边形ABCD是正方形, BC =1,对角线交点记作O,点E是边BC延长线上一点.联结OE交CD边于F,设,,求关于的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线——过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
(2)如果将问题1中的条件“四边形ABCD是正方形,BC =1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图25-2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC =1”进一步改为:“四边形ABCD是梯形,AD∥BC,,,(其中,,为常量)”其余条件不变(如图25-3),请你写出条件再次改变后关于的函数解析式以及相应的推导过程.
解:(1)∵四边形ABCD是正方形,∴OB=OD.
∵OM⊥BC,∴∠OMB=∠DCB=,∴OM∥DC.
∴OMDC,CMBC.∵OM∥DC,∴,
即,解得.定义域为.
(2)().
(3)AD∥BC,,.
过点O作ON∥CD,交BC于点N,∴,∴.
∵ON∥CD,,∴,∴.
∵ON∥CD,∴,即 .
∴关于的函数解析式为().
【预测题】12、已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位,求平移后的图象的解析式;
(3) 在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象。请你结合这个新的图像回答:当直线y=x+b (b解:(1)由题意得,Δ=16-8(k-1)≥0.∴k≤3.∵k为正整数,∴k=1,2,3.
(2)当k=1时,方程2x2+4x+k-1=0有一个根为零;
当k=2时,方程2x2+4x+k-1=0无整数根;
当k=3时,方程2x2+4x+k-1=0有两个非零的整数根.
综上所述,k=1和k=2不合题意,舍去;k=3符合题意.
当k=3时,二次函数为y=2x2+4x+2,把它的图象向下平移8个单位长度得到的图象的解析式为y=2x2+4x-6.
(3)设二次函数y=2x2+4x-6的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
当直线经过A点时,可得;
当直线经过B点时,可得.
由图象可知,符合题意的b(b<3)的取值范围为.
【预测题】13、如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
解:(1)设抛物线解析式为,把代入得.
,顶点
(2)假设满足条件的点存在,依题意设,
由求得直线的解析式为,
它与轴的夹角为,设的中垂线交于,则.
则,点到的距离为.
又..
平方并整理得:,.
存在满足条件的点,的坐标为.
(3)由上求得.
①若抛物线向上平移,可设解析式为.
当时,.
当时,.或.
.
②若抛物线向下移,可设解析式为.
由,
有.,.
∴向上最多可平移72个单位长,向下最多可平移个单位长.
【预测题】14、如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
解:(1)过点D作DE⊥x轴,垂足为E,则△PED∽△COP,∴
,,故D(t+1,)
(2)S=
∴当t=2时,S最大,最大值为1
(3)∵∠CPD=900,∴∠DPA+∠CPO=900,∴∠DPA≠900,故有以下两种情况:
①当∠PDA=900时,由勾股定理得,又,
,,
即,解得,(不合题意,舍去)
②当∠PAD=900时,点D在BA上,故AE=3-t,得t=3
综上,经过2秒或3秒时,△PAD是直角三角形;
(4);
【预测题】15、设抛物线与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90°。
(1)求m的值;
(2)求抛物线的解析式,并验证点D(1,-3 )是否在抛物线上;
(3)已知过点A的直线交抛物线于另一点E. 问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标. 若不存在,请说明理由。
解:(1)令x=0,得y=-2 ∴C(0,-2)
∵∠ACB=90°,CO⊥AB ,∴△AOC ∽△COB ,∴OA·OB=OC2
∴OB= ∴m=4
(2)将A(-1,0),B(4,0)代入,解得
∴抛物线的解析式为……(2分)
当x=1时,=-3,∴点D(1,-3)在抛物线上。
(3)由 得 ,∴E(6,7)
过E作EH⊥x轴于H,则H(6,0),
∴ AH=EH=7 ∴∠EAH=45°
作DF⊥x轴于F,则F(1,0)
∴BF=DF=3 ∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则,∴
∴,∴……(2分)
②若△∽△BAE,则,∴
∴ ∴……(2分)
综合①、②,得点P的坐标为:
【预测题】16、如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AB于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
解:(1)四边形ABCE是菱形。
∵△ECD是由△ABC沿BC平移得到的,∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,又∵AB=BC,∴四边形ABCE是菱形 .
(2)①四边形PQED的面积不发生变化。
方法一:∵ABCE是菱形,∴AC⊥BE,OC=AC=3,∵BC=5,∴BO=4,
过A作AH⊥BD于H,(如图1).∵S△ABC=BC×AH=AC×BO,
即:×5×AH=×6×4,∴AH=.
【或 ∵∠AHC=∠BOC=90°,∠BCA公用,∴△AHC∽△BOC,∴AH:BO=AC:BC,
即:AH:4=6:5,∴AH=.】
由菱形的对称性知,△PBO≌△QEO,∴BP=QE,
∴S四边形PQED=(QE+PD)×QR=(BP+PD)×AH=BD×AH=×10×=24.
方法二: 由菱形的对称性知,△PBO≌△QEO,∴S△PBO= S△QEO,
∵△ECD是由△ABC平移得到得,∴ED∥AC,ED=AC=6,
又∵BE⊥AC,∴BE⊥ED,
∴S四边形PQED=S△QEO+S四边形POED=S△PBO+S四边形POED=S△BED
=×BE×ED=×8×6=24.
②方法一:如图2,当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,∴∠2>∠3,∴∠2不与∠3对应,∴∠2与∠1对应,
即∠2=∠1,∴OP=OC=3,过O作OG⊥BC于G,则G为PC的中点,△OGC∽△BOC,
∴CG:CO=CO:BC,即:CG:3=3:5,∴CG=,
∴PB=BC-PC=BC-2CG=5-2×=.
方法二:如图3,当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,∴∠2>∠3,
∴∠2不与∠3对应,∴∠2与∠1对应,
∴QR:BO=PR:OC,即::4=PR:3,∴PR=,
过E作EF⊥BD于F,设PB=x,则RF=QE=PB=x,
DF== EQ \R(,62-()2) =,
∴BD=PB+PR+RF+DF=x++x+=10,x=.
方法三: 如图4,若点P在BC上运动,使点R与C重合,
由菱形的对称性知,O为PQ的中点,∴CO是Rt△PCQ斜边上的中线,
∴CO=PO,∴∠OPC=∠OCP,此时,Rt△PQR∽Rt△CBO,
∴PR:CO=PQ:BC,即PR:3=6:5,∴PR=
∴PB=BC-PR=5-=.
(第2题)
第3题
图2
G
2 4 6 8 10
1210
8
6
4
2
y
O
x
图1
C Q→ B
D
A
P↓
G
F
E
D
C
B
A
B
A
O
1
1
-1
-1
x
y
A′
B′
y
B
A
O
1
1
-1
-1
x
C
B′
D
(备用图)
A
B
C
O
x
y
A
B
C
O
x
y
E
A
B
(C)
O
x
y
E
图25-3
图25-2
图25-1题图
A
B
C
O
x
y
D
F
H
P
E
(第14题)
【预测题】1、已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°,动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
(1)求直线AC的解析式;
(2)试求出当t为何值时,△OAC与△PAQ相似;
(3)若⊙P的半径为,⊙Q的半径为;当⊙P与对角线AC相切时,判断⊙Q与直线AC、BC的位置关系,并求出Q点坐标。
解:(1)
(2)①当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,①若∠APQ=90°,则△APQ∽△OCA,
∵t>2.5,∴符合条件.
②若∠AQP=90°,则△APQ∽△∠OAC,
∵t>2.5,∴符合条件.
综上可知,当时,△OAC与△APQ相似.
(3)⊙Q与直线AC、BC均相切,Q点坐标为()。
【预测题】2、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
解:(1);.(2)在中,,
.
设点的坐标为,其中,顶点,
∴设抛物线解析式为.
①如图①,当时,,.
解得(舍去);...解得.
抛物线的解析式为
②如图②,当时,,.
解得(舍去).
③当时,,这种情况不存在.
综上所述,符合条件的抛物线解析式是.
(3)存在点,使得四边形的周长最小.
如图③,作点关于轴的对称点,作点关于
轴的对称点,连接,分别与轴、轴交于
点,则点就是所求点.
,.
..又,,此时四边形的周长最小值是.
【预测题】3、如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.
(1)①试判断BG与2BP的大小关系,并说明理由;
②用x的代数式表示线段DG的长,并写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式,并求出S的最大值;
(3)以P、E、F为顶点的三角形与△EDG是否可能相似?如果能相似,请求出BP的长,如果不能,请说明理由。
解:(1)①在等边三角形ABC中,∠B=60°,∵PG⊥AB,
∴∠BGP=30°,∴BG=2BP.
②∵PF//AC,∴△PBF为等边三角形,∴BF=PF=PB=x.
又∵BG=2x,BD=1,∴DG=2x-1,∴0<2x-1≤1,∴.
(2)S=DE×DF=
=
当时,.
(3)①如图1,若∠PFE=Rt∠,则两三角形相似,
此时可得DF=DG
即
解得:.
②如图2,若∠PEF=Rt∠,则两三角形相似,
此时可得DF=EF=BP,
即.解得:.
【预测题】4、如图,二次函数的图像经过点,
且与轴交于点.
(1)试求此二次函数的解析式;
(2)试证明:(其中是原点);
(3)若是线段上的一个动点(不与、重合),过作轴的平行线,分别交此二次函数图像及轴于、两点,试问:是否存在这样的点,使?若存在,请求出点的坐标;若不存在,请说明理由。
解:(1)∵点与在二次函数图像上,
∴,解得,
∴二次函数解析式为.
(2)过作轴于点,由(1)得,则在中,,又在中,,
∵,∴.
(3)由与,可得直线的解析式为,
设,则,
∴.∴.
当,解得 (舍去),∴.
当,解得 (舍去),∴.
综上所述,存在满足条件的点,它们是与.
【预测题】5、如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6=,过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
解:(1)∵,CD=3,CQ=x,∴.
图象如图所示.
(2)方法一:,CP=8k-xk,CQ=x,
∴.∵抛物线顶点坐标是(4,12),
∴.解得.则点P的速度每秒厘米,AC=12厘米.
方法二:观察图象知,当x=4时,△PCQ面积为12.
此时PC=AC-AP=8k-4k=4k,CQ=4.∴由,得 .
解得.则点P的速度每秒厘米,AC=12厘米.
方法三:设y2的图象所在抛物线的解析式是.
∵图象过(0,0),(4,12),(8,0),
∴ 解得 ∴. ①
∵,CP=8k-xk,CQ=x,∴. ②
比较①②得.则点P的速度每秒厘米,AC=12厘米.
(3)①观察图象,知线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积).②由⑵得 .(方法二,)
∵EF=y2-y1,∴EF=,
∵二次项系数小于0,∴在范围,当时,最大.
【预测题】6、如图,在中,,、分别是边、
上的两个动点(不与、重合),且保持,以为边,在点的异侧作正方形.
(1)试求的面积;
(2)当边与重合时,求正方形的边长;
(3)设,与正方形重叠部分的面积为,试求关于的函数关系式,并写出定义域;
(4)当是等腰三角形时,请直接写出的长。
解:(1)过作于,∵,∴.
则在中,,∴.
(2)令此时正方形的边长为,则,解得.
(3)当时,.
当时,.
(4).
【预测题】7、如图已知点A (-2,4) 和点B (1,0)都在抛物线上.
(1)求、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′ 的交点为点C,试在轴上找点D,使得以点B′、C、D为顶点的三角形与相似.
解:(1)根据题意,得: 解得
(2)四边形A A′B′B为菱形,则A A′=B′B= AB=5
∵
=
∴ 向右平移5个单位的抛物线解析式为
(3)设D(x,0)根据题意,得:AB=5,
∵∠A=∠B B′A
ⅰ) △ABC∽△B′CD时,∠ABC=∠B′CD ,∴BD=6-x, 由 得 解得x=3, ∴D(3,0)
ⅱ)△ABC∽△B′DC时,
∴ 解得 ∴
【预测题】8、如 图,已知直角梯形ABCD中,AD∥BC,A B⊥BC ,AD=2,AB=8,
CD=10.
(1)求梯形ABCD的面积S;
(2)动点P从点B出发,以1cm/s的速度、沿B→A→D→C方向,向点C运动;动点Q从点C出发,以1cm/s的速度、沿C→D→A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由;
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
解:
在Rt△DCH中,
(2)①
经计算,PQ不平分梯形ABCD的面积
②
,-
【预测题】9、如图,⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(,0),CAB=90°,AC=AB,顶点A在⊙O上运动.
(1)当点A在x轴上时,求点C的坐标;
(2)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(3)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;
(4)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
解:(1)当点A的坐标为(1,0)时,AB=AC=-1,点C的坐标为(1,-1);
当点A的坐标为(-1,0)时,AB=AC=+1,点C的坐标为(-1,+1);
(2)直线BC与⊙O相切,过点O作OM⊥BC于点M,∴∠OBM=∠BOM=45°,
∴OM=OB·sin45°=1,∴直线BC与⊙O相切
(3)过点A作AE⊥OB于点E
在Rt△OAE中,AE2=OA2-OE2=1-x2,
在Rt△BAE中,AB2=AE2+BE2=(1-x2) +(-x)2=3-2x
∴S=AB·AC= AB2=(3-2x)=
其中-1≤x≤1,
当x=-1时,S的最大值为,
当x=1时,S的最小值为.
(4)①当点A位于第一象限时(如右图):
连接OA,并过点A作AE⊥OB于点E
∵直线AB与⊙O相切,∴∠OAB=90°,
又∵∠CAB=90°,∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线上,∴∠AOB=∠C=45°,
在Rt△OAE中,OE=AE=.点A的坐标为(,)
过A、B两点的直线为y=-x+.
②当点A位于第四象限时(如右图)
点A的坐标为(,-),过A、B两点的直线为y=x-.
【预测题】10、已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上,∴c=8,将A(-6,0)、B(2,0)代入表达式,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)依题意,AE=m,则BE=8-m,∵OA=6,OC=8,∴AC=10
∵EF∥AC ∴△BEF∽△BAC,∴= 即=,∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(4)存在.
理由:∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8 ∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.
【预测题】11、数学课上,张老师出示了问题1:如图25-1,四边形ABCD是正方形, BC =1,对角线交点记作O,点E是边BC延长线上一点.联结OE交CD边于F,设,,求关于的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线——过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
(2)如果将问题1中的条件“四边形ABCD是正方形,BC =1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图25-2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC =1”进一步改为:“四边形ABCD是梯形,AD∥BC,,,(其中,,为常量)”其余条件不变(如图25-3),请你写出条件再次改变后关于的函数解析式以及相应的推导过程.
解:(1)∵四边形ABCD是正方形,∴OB=OD.
∵OM⊥BC,∴∠OMB=∠DCB=,∴OM∥DC.
∴OMDC,CMBC.∵OM∥DC,∴,
即,解得.定义域为.
(2)().
(3)AD∥BC,,.
过点O作ON∥CD,交BC于点N,∴,∴.
∵ON∥CD,,∴,∴.
∵ON∥CD,∴,即 .
∴关于的函数解析式为().
【预测题】12、已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位,求平移后的图象的解析式;
(3) 在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象。请你结合这个新的图像回答:当直线y=x+b (b
(2)当k=1时,方程2x2+4x+k-1=0有一个根为零;
当k=2时,方程2x2+4x+k-1=0无整数根;
当k=3时,方程2x2+4x+k-1=0有两个非零的整数根.
综上所述,k=1和k=2不合题意,舍去;k=3符合题意.
当k=3时,二次函数为y=2x2+4x+2,把它的图象向下平移8个单位长度得到的图象的解析式为y=2x2+4x-6.
(3)设二次函数y=2x2+4x-6的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
当直线经过A点时,可得;
当直线经过B点时,可得.
由图象可知,符合题意的b(b<3)的取值范围为.
【预测题】13、如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
解:(1)设抛物线解析式为,把代入得.
,顶点
(2)假设满足条件的点存在,依题意设,
由求得直线的解析式为,
它与轴的夹角为,设的中垂线交于,则.
则,点到的距离为.
又..
平方并整理得:,.
存在满足条件的点,的坐标为.
(3)由上求得.
①若抛物线向上平移,可设解析式为.
当时,.
当时,.或.
.
②若抛物线向下移,可设解析式为.
由,
有.,.
∴向上最多可平移72个单位长,向下最多可平移个单位长.
【预测题】14、如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
解:(1)过点D作DE⊥x轴,垂足为E,则△PED∽△COP,∴
,,故D(t+1,)
(2)S=
∴当t=2时,S最大,最大值为1
(3)∵∠CPD=900,∴∠DPA+∠CPO=900,∴∠DPA≠900,故有以下两种情况:
①当∠PDA=900时,由勾股定理得,又,
,,
即,解得,(不合题意,舍去)
②当∠PAD=900时,点D在BA上,故AE=3-t,得t=3
综上,经过2秒或3秒时,△PAD是直角三角形;
(4);
【预测题】15、设抛物线与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90°。
(1)求m的值;
(2)求抛物线的解析式,并验证点D(1,-3 )是否在抛物线上;
(3)已知过点A的直线交抛物线于另一点E. 问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标. 若不存在,请说明理由。
解:(1)令x=0,得y=-2 ∴C(0,-2)
∵∠ACB=90°,CO⊥AB ,∴△AOC ∽△COB ,∴OA·OB=OC2
∴OB= ∴m=4
(2)将A(-1,0),B(4,0)代入,解得
∴抛物线的解析式为……(2分)
当x=1时,=-3,∴点D(1,-3)在抛物线上。
(3)由 得 ,∴E(6,7)
过E作EH⊥x轴于H,则H(6,0),
∴ AH=EH=7 ∴∠EAH=45°
作DF⊥x轴于F,则F(1,0)
∴BF=DF=3 ∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则,∴
∴,∴……(2分)
②若△∽△BAE,则,∴
∴ ∴……(2分)
综合①、②,得点P的坐标为:
【预测题】16、如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AB于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
解:(1)四边形ABCE是菱形。
∵△ECD是由△ABC沿BC平移得到的,∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,又∵AB=BC,∴四边形ABCE是菱形 .
(2)①四边形PQED的面积不发生变化。
方法一:∵ABCE是菱形,∴AC⊥BE,OC=AC=3,∵BC=5,∴BO=4,
过A作AH⊥BD于H,(如图1).∵S△ABC=BC×AH=AC×BO,
即:×5×AH=×6×4,∴AH=.
【或 ∵∠AHC=∠BOC=90°,∠BCA公用,∴△AHC∽△BOC,∴AH:BO=AC:BC,
即:AH:4=6:5,∴AH=.】
由菱形的对称性知,△PBO≌△QEO,∴BP=QE,
∴S四边形PQED=(QE+PD)×QR=(BP+PD)×AH=BD×AH=×10×=24.
方法二: 由菱形的对称性知,△PBO≌△QEO,∴S△PBO= S△QEO,
∵△ECD是由△ABC平移得到得,∴ED∥AC,ED=AC=6,
又∵BE⊥AC,∴BE⊥ED,
∴S四边形PQED=S△QEO+S四边形POED=S△PBO+S四边形POED=S△BED
=×BE×ED=×8×6=24.
②方法一:如图2,当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,∴∠2>∠3,∴∠2不与∠3对应,∴∠2与∠1对应,
即∠2=∠1,∴OP=OC=3,过O作OG⊥BC于G,则G为PC的中点,△OGC∽△BOC,
∴CG:CO=CO:BC,即:CG:3=3:5,∴CG=,
∴PB=BC-PC=BC-2CG=5-2×=.
方法二:如图3,当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,∴∠2>∠3,
∴∠2不与∠3对应,∴∠2与∠1对应,
∴QR:BO=PR:OC,即::4=PR:3,∴PR=,
过E作EF⊥BD于F,设PB=x,则RF=QE=PB=x,
DF== EQ \R(,62-()2) =,
∴BD=PB+PR+RF+DF=x++x+=10,x=.
方法三: 如图4,若点P在BC上运动,使点R与C重合,
由菱形的对称性知,O为PQ的中点,∴CO是Rt△PCQ斜边上的中线,
∴CO=PO,∴∠OPC=∠OCP,此时,Rt△PQR∽Rt△CBO,
∴PR:CO=PQ:BC,即PR:3=6:5,∴PR=
∴PB=BC-PR=5-=.
(第2题)
第3题
图2
G
2 4 6 8 10
1210
8
6
4
2
y
O
x
图1
C Q→ B
D
A
P↓
G
F
E
D
C
B
A
B
A
O
1
1
-1
-1
x
y
A′
B′
y
B
A
O
1
1
-1
-1
x
C
B′
D
(备用图)
A
B
C
O
x
y
A
B
C
O
x
y
E
A
B
(C)
O
x
y
E
图25-3
图25-2
图25-1题图
A
B
C
O
x
y
D
F
H
P
E
(第14题)
同课章节目录
