6.3二项式定理(课件)-2021-2022学年数学人教A版2019选择性必修第三册(共22张PPT)
文档属性
| 名称 | 6.3二项式定理(课件)-2021-2022学年数学人教A版2019选择性必修第三册(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 820.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
6.3.1 二项式定理
一、提出问题,引发思考
如果今天是周二,那么再过8天后,是周几?再过是周几?
因为8=7+1,再过8天后,是周三
二、回顾已知,加强印象
由完全平方公式
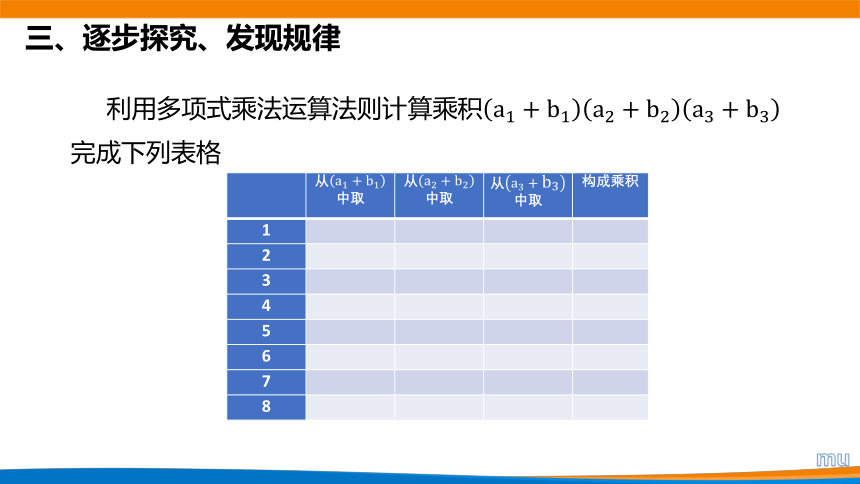
三、逐步探究、发现规律
利用多项式乘法运算法则计算乘积
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
完成下列表格
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
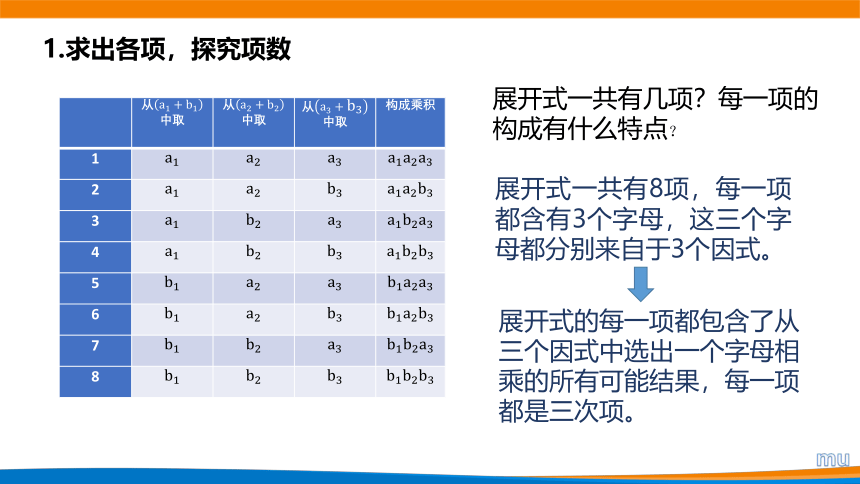
展开式一共有几项?每一项的构成有什么特点?
展开式一共有8项,每一项都含有3个字母,这三个字母都分别来自于3个因式。
展开式的每一项都包含了从三个因式中选出一个字母相乘的所有可能结果,每一项都是三次项。
1.求出各项,探究项数
你能利用计数原理,来证明展开式拥有8项吗?
根据分步乘法计数原理,从三个因式中分别选出一个字母,因此,最终的展开式一共有种结果,即拥有8项。
取出
取出
取出
1.求出各项,探究项数
2.合并同类项,探究系数
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
令表格中, ,填充在最后一列。
变为即
展开式变为
回顾、的选取过程
2.合并同类项,探究系数
同时选取,即都不选b
有种取法,形成1个
两个因式取,即选一个因式取b
,形成3个
一个因式取即选两个因式取b
同时选取b,即都不选
3.找寻规律
因此
对于的展开结果,回答问题。
(1)此时等式右边展开式中有几项?
(2)观察展开式的每一项,字母a、b的指数有什么变化规律?
(3)如何将每一项中a、b的变化写成一个与k (k=0,1,2)有关的通式?
有4项
字母a的指数从3开始递减至0,字母b的指数从0递増至3
(k=0,1,2)
四、猜测定理,类比证明
你能猜测出n个相乘的结果吗?
类比的研究方法,对猜想的正确性加以说明
1.求出各项,探究项数
是n个 相乘
由分步乘法计数原理
从每一个中都选择一个或者b
的展开式一共有
其中,
每一项都可以表示为的形式。
2.合并同类项,探究系数
的出现,是在n个因式中挑选n-k个因式取出,其余k个因式取出b
出现的次数=从n个因式中取出k个b的组合数
合并同类项后,的系数是
从而,猜想正确!
3.探求规律
(1)此时展开式共有几项?是n项吗
(2)展开式的每一项,字母a、b的指数有什么变化规律?
(3)展开式的第一项是什么?第二项?第n项是?最后一项是?
(4)你能发现项数与k的关系吗?
展开式共有n+1项
字母a的指数从n开始递减至0,字母b的指数从0递増至n
第1项是,第2项是,第n项是,最后一项是第n+1项,为
项数=k+1
五、得出定理
称为二项式定理,等式右边的式子称为的二项展开式,的二项展开式共有n+1项,其中各项的系数称为二项式系数,式中,叫做二项展开式的通项,用来表示,即通项为展开式的第k+1项:
五、得出定理
若设你能写出对应的展开式吗?
你能写出的展开式吗?
六、回归问题,应用解决
例:如果今天是周二,那么再过天后,是周几?
除了第一项外,每一项都是7的倍数
除以7余1,那么再过天后是周三。
应用公式:
七、强化训练,巩固提升
【例1】求的展开式
解:根据二项式定理,
【例2】(1)求的展开式的第4项的系数
七、强化训练,巩固提升
解:第4项是
则展开式第4项系数为280
区别二项式系数和系数!
第4项的二项式系数是?
第4项的二项式系数为
(2)求的展开式中的系数是?
解:通项为
求的系数,即令3-k=2,k=1,
因此,的系数为:(-1)
七、强化训练,巩固提升
八、小结归纳
1.探讨的展开式,的展开式,得到二项式定理、二项式系数、通项公式
2.明确 的展开式
3.明确二项式系数与系数的区别
4.能利用二项式定理解决二项式的展开问题,能求出展开式中的任意一项。
九、作业布置
必做:教材P31练习1、2、4
选做:教材P31练习3、5
谢 谢 大 家 !
6.3.1 二项式定理
一、提出问题,引发思考
如果今天是周二,那么再过8天后,是周几?再过是周几?
因为8=7+1,再过8天后,是周三
二、回顾已知,加强印象
由完全平方公式
三、逐步探究、发现规律
利用多项式乘法运算法则计算乘积
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
完成下列表格
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
展开式一共有几项?每一项的构成有什么特点?
展开式一共有8项,每一项都含有3个字母,这三个字母都分别来自于3个因式。
展开式的每一项都包含了从三个因式中选出一个字母相乘的所有可能结果,每一项都是三次项。
1.求出各项,探究项数
你能利用计数原理,来证明展开式拥有8项吗?
根据分步乘法计数原理,从三个因式中分别选出一个字母,因此,最终的展开式一共有种结果,即拥有8项。
取出
取出
取出
1.求出各项,探究项数
2.合并同类项,探究系数
从中取 从中取 从中取 构成乘积
1
2
3
4
5
6
7
8
令表格中, ,填充在最后一列。
变为即
展开式变为
回顾、的选取过程
2.合并同类项,探究系数
同时选取,即都不选b
有种取法,形成1个
两个因式取,即选一个因式取b
,形成3个
一个因式取即选两个因式取b
同时选取b,即都不选
3.找寻规律
因此
对于的展开结果,回答问题。
(1)此时等式右边展开式中有几项?
(2)观察展开式的每一项,字母a、b的指数有什么变化规律?
(3)如何将每一项中a、b的变化写成一个与k (k=0,1,2)有关的通式?
有4项
字母a的指数从3开始递减至0,字母b的指数从0递増至3
(k=0,1,2)
四、猜测定理,类比证明
你能猜测出n个相乘的结果吗?
类比的研究方法,对猜想的正确性加以说明
1.求出各项,探究项数
是n个 相乘
由分步乘法计数原理
从每一个中都选择一个或者b
的展开式一共有
其中,
每一项都可以表示为的形式。
2.合并同类项,探究系数
的出现,是在n个因式中挑选n-k个因式取出,其余k个因式取出b
出现的次数=从n个因式中取出k个b的组合数
合并同类项后,的系数是
从而,猜想正确!
3.探求规律
(1)此时展开式共有几项?是n项吗
(2)展开式的每一项,字母a、b的指数有什么变化规律?
(3)展开式的第一项是什么?第二项?第n项是?最后一项是?
(4)你能发现项数与k的关系吗?
展开式共有n+1项
字母a的指数从n开始递减至0,字母b的指数从0递増至n
第1项是,第2项是,第n项是,最后一项是第n+1项,为
项数=k+1
五、得出定理
称为二项式定理,等式右边的式子称为的二项展开式,的二项展开式共有n+1项,其中各项的系数称为二项式系数,式中,叫做二项展开式的通项,用来表示,即通项为展开式的第k+1项:
五、得出定理
若设你能写出对应的展开式吗?
你能写出的展开式吗?
六、回归问题,应用解决
例:如果今天是周二,那么再过天后,是周几?
除了第一项外,每一项都是7的倍数
除以7余1,那么再过天后是周三。
应用公式:
七、强化训练,巩固提升
【例1】求的展开式
解:根据二项式定理,
【例2】(1)求的展开式的第4项的系数
七、强化训练,巩固提升
解:第4项是
则展开式第4项系数为280
区别二项式系数和系数!
第4项的二项式系数是?
第4项的二项式系数为
(2)求的展开式中的系数是?
解:通项为
求的系数,即令3-k=2,k=1,
因此,的系数为:(-1)
七、强化训练,巩固提升
八、小结归纳
1.探讨的展开式,的展开式,得到二项式定理、二项式系数、通项公式
2.明确 的展开式
3.明确二项式系数与系数的区别
4.能利用二项式定理解决二项式的展开问题,能求出展开式中的任意一项。
九、作业布置
必做:教材P31练习1、2、4
选做:教材P31练习3、5
谢 谢 大 家 !
