沪科版数学八年级下册 第17章 17.1一元二次方程(通用)课件(共22张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 第17章 17.1一元二次方程(通用)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 10:30:44 | ||
图片预览








文档简介
(共22张PPT)
第17章 一元二次方程(通用)
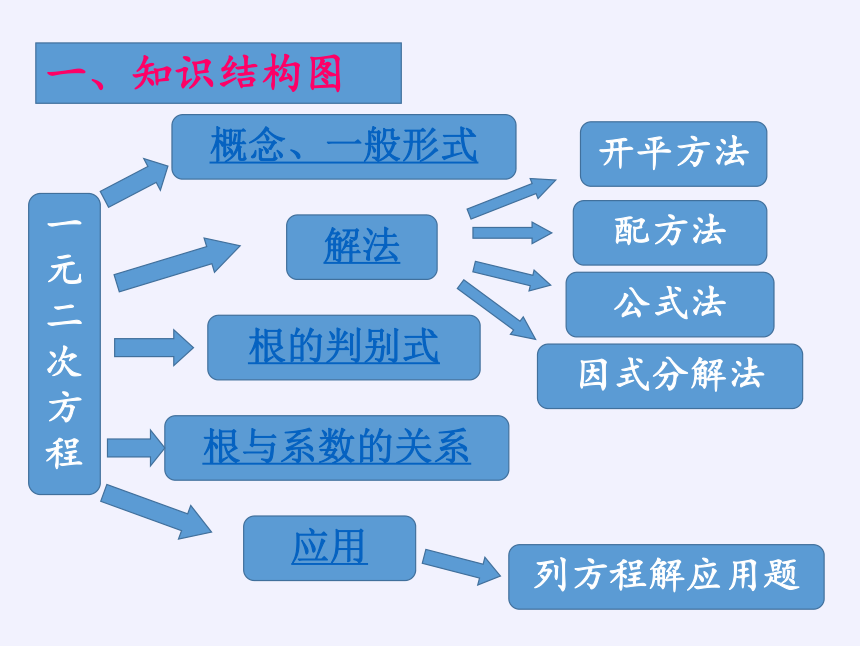
一、知识结构图
一元二次方程
概念、一般形式
根的判别式
根与系数的关系
解法
应用
开平方法
配方法
公式法
因式分解法
列方程解应用题
二、主要知识回顾
(一)、概念、形式
概念:只含有一个未知数,并且未知数
的最高次数是2的整式方程叫做
一元二次方程.
一般形式:ax2+bx+c=0
(a≠0)
练一练:
1.下列方程中,是一元二次方程的是( )
A. x2+ =0 B. ax2+bx+c
C. (x-1)(x+2)=1 D. 3x2-2xy=0
2.已知关于x的一元二次方程
(a-1)x2+x+a2-1=0的常数项为0,则a的值为
( )
A. 1 B. -1 C. 1或-1 D. 0.5
C
B
返回
(二)、解法
1.直接开平方法:符合x2=a(a≥0)的形
式的一元二次方程都可
用直接开平方法
2.配方法: ①二次项系数化为1
②配一次项系数一半的平方
③用直接开平方法求解
3.公式法: ①原方程整理成一般形式
②确定b2-4ac≥0
③运用求根公式
(b2-4ac≥0)求解
4.因式分解法: ①先因式分解
②再转化为两个一元一
次方程求解
解下列方程:
(1)x2-6x+9=4(直接开平方法);
(2)x2-4x-6=0(配方法);
(3)(x-3)(x-4)=5x(公式法);
(4)(5x-1)2=3(1-5x)(因式分解法).
返回
(三)、根的判别式
一元二次方程ax2+bx+c=0(a≠0)的根
的判别式:△=b2-4ac≥0
△>0 方程有两个不相等的实数根
△=0 方程有两个相等的实数根
△<0 方程没有实数根
想一想:
1.下列方程中,有两不等实根的是 ( )
A. x2-2x-1=0 B.x2-2x+3=0
C. x2=2 x-3 D.x2-4x+4=0
2.方程x2-4mx=2-m(m为常数)根的情况是( )
A.有两不等实根 B.有两等实根
C.没有实数根 D.无法判断
A
A
返回
(四)、根与系数的关系
如果一元二次方程ax2+bx+c=0
(a≠0)的两个根为x1、x2,那么
x1+x2=- ,x1x2=
注意:隐含条件△≥0
已知一元二次方程x2-3x-1=0的两个根
分别为x1,x2则x1+x2的值为 ()x1x2的值为()
试一试:
返回
1.可化为一元一次方程的分式方程
注意:验根
2.列方程解应用题:
步骤:审、设、列、求、验、答
注意:①关键是找出等量关系列出方程;
② 验根时既要检验是否是原方程
的根,又要检验是否符合题意.
(五)、应用
1.若两个连续整数的积是20,则这两个数是( )
A.4和5 B.-5和-4
C.4和5或-5和-4 D. 4和 5
2.某药品经过两次降价,每瓶零售价由168元降为128元,已知两次降价的百分率相同,每次降价的百分率为x,由题意可列方程为( )
A.168(1+x)2=128 B.168(1-x)2=128
C.168(1-2x)2=128 D.168(1-x2)=128
C
B
典例讲解1
解下列方程:(1)x2+x-1=0;
(2)(x-3)2+2x(x-3)=0.
典例讲解2
若关于x的方程(m2-1)x2-2(m+2)x+1=0有实数根,求m的取值范围.
典例讲解3
我校团委准备举办学生绘画展览,为美化画面,在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面积相等,求彩纸的宽度.
能力小测试:
1.不论x取何值时,2x-x2-3的值 ( )
A.不小于-2 B.不大于-2
C.有最小值-2 D.有可能大于零
2.下列方程中,无论a取何值,总是关于x的一
元二次方程的是( )
A.(2x-1)(x2+3)=2x2-a B.ax2-3x+9=0
C.ax2+x=x2-1 D.(3a2+4)x2-2=0
B
D
3. 已知关于x的一元二次方程kx2-4kx+k-5=0
有两个相等的实数根,则k=______.
-
4.用适当的方法解下列方程:
(1)3x(x-1)=1-x;
(2)x2-2x-11=0;
(3)2x2-5x-1=0.
(1)x1=1
x2=-
(2)x1=1+2
x2=1-2
(3)x1=
x2=-
5.A、B两地相距18km,甲工程队要在A、B两地间铺一条输送天然气管道,乙工程队要在A、B两地间铺设一条输油管道.已知甲工程队每周比乙工程队少铺设1km,甲工程队提前3周开工,结果两队同时完成任务,求甲、乙工程队每周各铺设多少千米?
甲工程队每周铺设2km
乙工程队每周铺设3km
归纳小结
1.你能把本章的内容作一个书面整理吗?
2.利用方程(组)解决实际问题的关键是什么?
3.本章有哪些地方用到了“化归方法”这一重要数学思想方法是最简二次根式、同类二次根式?
谢 谢
第17章 一元二次方程(通用)
一、知识结构图
一元二次方程
概念、一般形式
根的判别式
根与系数的关系
解法
应用
开平方法
配方法
公式法
因式分解法
列方程解应用题
二、主要知识回顾
(一)、概念、形式
概念:只含有一个未知数,并且未知数
的最高次数是2的整式方程叫做
一元二次方程.
一般形式:ax2+bx+c=0
(a≠0)
练一练:
1.下列方程中,是一元二次方程的是( )
A. x2+ =0 B. ax2+bx+c
C. (x-1)(x+2)=1 D. 3x2-2xy=0
2.已知关于x的一元二次方程
(a-1)x2+x+a2-1=0的常数项为0,则a的值为
( )
A. 1 B. -1 C. 1或-1 D. 0.5
C
B
返回
(二)、解法
1.直接开平方法:符合x2=a(a≥0)的形
式的一元二次方程都可
用直接开平方法
2.配方法: ①二次项系数化为1
②配一次项系数一半的平方
③用直接开平方法求解
3.公式法: ①原方程整理成一般形式
②确定b2-4ac≥0
③运用求根公式
(b2-4ac≥0)求解
4.因式分解法: ①先因式分解
②再转化为两个一元一
次方程求解
解下列方程:
(1)x2-6x+9=4(直接开平方法);
(2)x2-4x-6=0(配方法);
(3)(x-3)(x-4)=5x(公式法);
(4)(5x-1)2=3(1-5x)(因式分解法).
返回
(三)、根的判别式
一元二次方程ax2+bx+c=0(a≠0)的根
的判别式:△=b2-4ac≥0
△>0 方程有两个不相等的实数根
△=0 方程有两个相等的实数根
△<0 方程没有实数根
想一想:
1.下列方程中,有两不等实根的是 ( )
A. x2-2x-1=0 B.x2-2x+3=0
C. x2=2 x-3 D.x2-4x+4=0
2.方程x2-4mx=2-m(m为常数)根的情况是( )
A.有两不等实根 B.有两等实根
C.没有实数根 D.无法判断
A
A
返回
(四)、根与系数的关系
如果一元二次方程ax2+bx+c=0
(a≠0)的两个根为x1、x2,那么
x1+x2=- ,x1x2=
注意:隐含条件△≥0
已知一元二次方程x2-3x-1=0的两个根
分别为x1,x2则x1+x2的值为 ()x1x2的值为()
试一试:
返回
1.可化为一元一次方程的分式方程
注意:验根
2.列方程解应用题:
步骤:审、设、列、求、验、答
注意:①关键是找出等量关系列出方程;
② 验根时既要检验是否是原方程
的根,又要检验是否符合题意.
(五)、应用
1.若两个连续整数的积是20,则这两个数是( )
A.4和5 B.-5和-4
C.4和5或-5和-4 D. 4和 5
2.某药品经过两次降价,每瓶零售价由168元降为128元,已知两次降价的百分率相同,每次降价的百分率为x,由题意可列方程为( )
A.168(1+x)2=128 B.168(1-x)2=128
C.168(1-2x)2=128 D.168(1-x2)=128
C
B
典例讲解1
解下列方程:(1)x2+x-1=0;
(2)(x-3)2+2x(x-3)=0.
典例讲解2
若关于x的方程(m2-1)x2-2(m+2)x+1=0有实数根,求m的取值范围.
典例讲解3
我校团委准备举办学生绘画展览,为美化画面,在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面积相等,求彩纸的宽度.
能力小测试:
1.不论x取何值时,2x-x2-3的值 ( )
A.不小于-2 B.不大于-2
C.有最小值-2 D.有可能大于零
2.下列方程中,无论a取何值,总是关于x的一
元二次方程的是( )
A.(2x-1)(x2+3)=2x2-a B.ax2-3x+9=0
C.ax2+x=x2-1 D.(3a2+4)x2-2=0
B
D
3. 已知关于x的一元二次方程kx2-4kx+k-5=0
有两个相等的实数根,则k=______.
-
4.用适当的方法解下列方程:
(1)3x(x-1)=1-x;
(2)x2-2x-11=0;
(3)2x2-5x-1=0.
(1)x1=1
x2=-
(2)x1=1+2
x2=1-2
(3)x1=
x2=-
5.A、B两地相距18km,甲工程队要在A、B两地间铺一条输送天然气管道,乙工程队要在A、B两地间铺设一条输油管道.已知甲工程队每周比乙工程队少铺设1km,甲工程队提前3周开工,结果两队同时完成任务,求甲、乙工程队每周各铺设多少千米?
甲工程队每周铺设2km
乙工程队每周铺设3km
归纳小结
1.你能把本章的内容作一个书面整理吗?
2.利用方程(组)解决实际问题的关键是什么?
3.本章有哪些地方用到了“化归方法”这一重要数学思想方法是最简二次根式、同类二次根式?
谢 谢
