沪科版数学八年级下册 17.1 一元二次方程课件(共22张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 17.1 一元二次方程课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 13:31:32 | ||
图片预览





文档简介
(共22张PPT)
17.1 一元二次方程
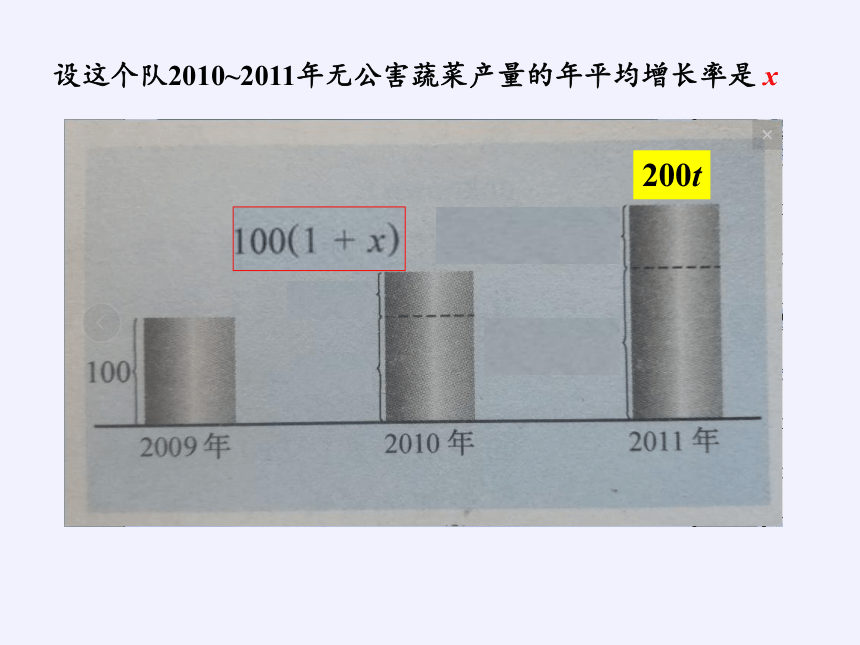
问题1 某蔬菜队2009年全年无公害蔬菜产量为100t,计划2011年无公害蔬菜的产量比2009年翻一番(即为200t)。要实现这一目标,2010年和2011年无公害蔬菜产量的年平均增长率应是多少?
翻一番
翻一番
设这个队2010~2011年无公害蔬菜产量的年平均增长率是 x
200t
100+100x=100(1+x)
100(1+x)+100(1+x) x=100(1+x)
分析:设这个队2010~2011年无公害蔬菜产量的年平均增长率是 x ,那么:
2010年无公害蔬菜产量为:
2011年无公害蔬菜产量为:
解:设这个队2010-2011年无公害蔬菜产量的年平均增长率是x,那么;2010年无公害蔬菜产量为100+100x=100(1+x)(t);2011年无公害蔬菜产量为100(1+x)+100(1+x) x=100(1+x) (t)。
根据题意,2011年无公害蔬菜产量为200t,得
100(1+x) =200,
即 (1+x) =2。
整理,得
x + 2x – 1 = 0。
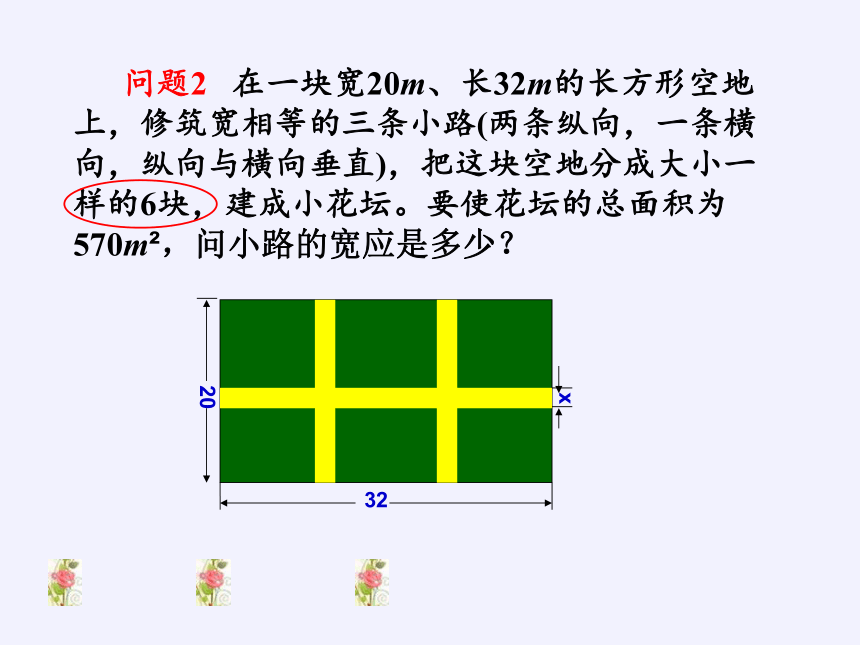
问题2 在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把这块空地分成大小一样的6块,建成小花坛。要使花坛的总面积为570m ,问小路的宽应是多少?
32
20
x
解:设小路的宽是xm,
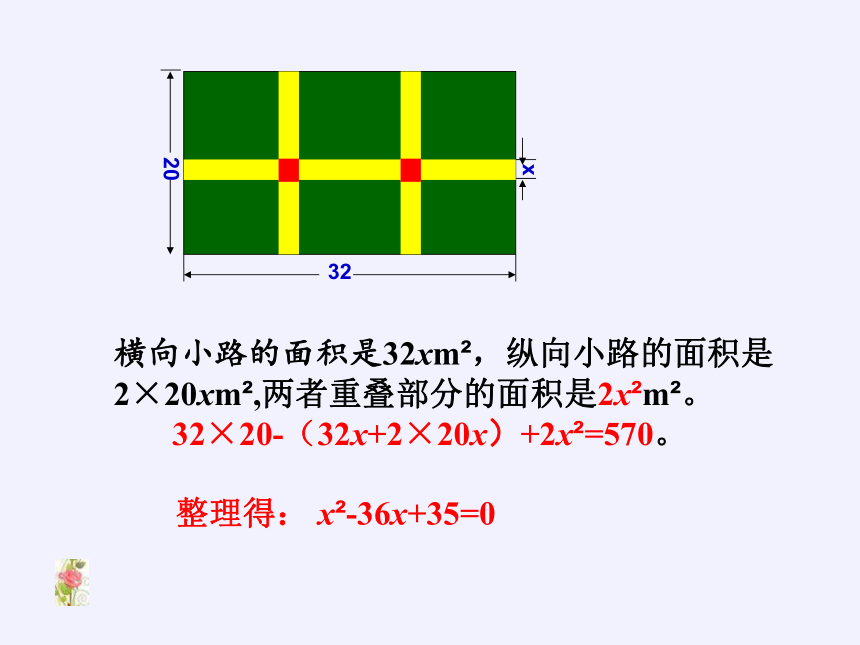
则横向小路的面积是32xm ,纵向小路的面积是2×20xm ,两者重叠部分的面积是2x m 。
由于花坛的总面积是570m ,则
32×20-(32x+2×20x)+2x =570。
整理,得
x -36x+35=0。
32
20
x
横向小路的面积是32xm ,纵向小路的面积是2×20xm ,两者重叠部分的面积是2x m 。
32×20-(32x+2×20x)+2x =570。
32
20
x
整理得: x -36x+35=0
32
20
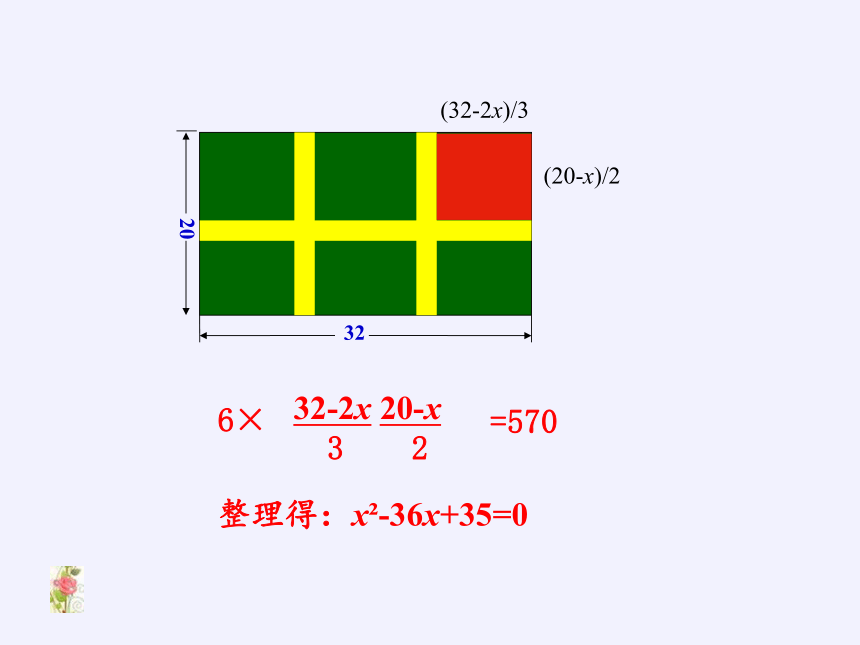
(20-x)/2
(32-2x)/3
32-2x 20-x
3 2
=570
6×
整理得:x -36x+35=0
(20-x)(32-2x)=570
32-2x
20-x
32
20
整理得:x -36x+35=0
③都是整式方程
①只含一个未知数
②未知数的最高次数是2
共同特点:
x +2x-1=0
x -36x+35=0
这两个方程有什么共同点?
回忆并说出一元一次方程的概念。
不忘老朋友
只含有一个未知数,且未知数的最高次数是1的整式方程,叫一元一次方程。
标准形式是 a x+ b =0(a,b为常数,且a≠0)。
③都是整式方程
①只含一个未知数
②未知数的最高次数是2
共同特点:
x +2x-1=0
x -36x+35=0
这两个方程有什么共同点?
一元二次方程
一元二次方程的概念
只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程叫做一元二次方程。
结识新朋友
下列方程中哪些是一元二次方程?
是分式
是二次根式
刷题中……
一般形式(标准形式):
ax2+ bx+ c= 0 (a,b,c为常数,a≠0)
其中ax2 bx c
a b
二次项
一次项
常数项
二次项系数
一次项系数
“=”的右边必须整理成0.
ax2+bx =0 (a≠0,b≠0)
完全的一元二次方程:
ax2+bx+c =0 (a≠0, b≠0, c≠0)
不完全的一 元二次方程:
ax2+c =0 (a≠0,c≠0)
ax2=0 (a≠0)
归纳:
一元二次方程的一般形式: ax2+bx+c=0 (a≠0)
3.方程(m+1) x |4m|-2 + 3mx-1=0是关于x的
一元二次方程,则m =
2.下列方程中,无论a为何值,总是关于x的一元二次方程的是( )
A.(2x-1)(x2+3)=2x2 - a B.ax2 + 2x +4=0
C.ax2 + x = x2-1 D.(a2+1)x2=0
行家看门道
1.关于x的方程(k2-1)x2 + 2 (k-1) x + 2=0,
当k 时,是一元二次方程;
当k 时,是一元一次方程。
例1 把方程3x(x-1)=2(x-2)-4化成一般形式,并写出它的二次项系数、一次项系数及常数项。
解: 去括号,得
3x -3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x -5x+8=0.
它的二次项系数是3,一次项系数是-5,
常数项是8。
例题解析
※什么叫方程的根?
※能够使方程左右两边相等的未知数的值,
叫方程的根。
登高望远
例2 已知x=0是关于x的一元二次方程,(m-1)x2 + x+ m2-1=0的一个根,求m的值,并判断x =3是不是方程的根。
已知x=0是关于x的一元二次方程
(m-1)x2 +x +m2-1=0的一个根,求m的值,
并判断x=3是不是方程的根。
这个方程还有没有其它的根?如何去求?
谢 谢
17.1 一元二次方程
问题1 某蔬菜队2009年全年无公害蔬菜产量为100t,计划2011年无公害蔬菜的产量比2009年翻一番(即为200t)。要实现这一目标,2010年和2011年无公害蔬菜产量的年平均增长率应是多少?
翻一番
翻一番
设这个队2010~2011年无公害蔬菜产量的年平均增长率是 x
200t
100+100x=100(1+x)
100(1+x)+100(1+x) x=100(1+x)
分析:设这个队2010~2011年无公害蔬菜产量的年平均增长率是 x ,那么:
2010年无公害蔬菜产量为:
2011年无公害蔬菜产量为:
解:设这个队2010-2011年无公害蔬菜产量的年平均增长率是x,那么;2010年无公害蔬菜产量为100+100x=100(1+x)(t);2011年无公害蔬菜产量为100(1+x)+100(1+x) x=100(1+x) (t)。
根据题意,2011年无公害蔬菜产量为200t,得
100(1+x) =200,
即 (1+x) =2。
整理,得
x + 2x – 1 = 0。
问题2 在一块宽20m、长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把这块空地分成大小一样的6块,建成小花坛。要使花坛的总面积为570m ,问小路的宽应是多少?
32
20
x
解:设小路的宽是xm,
则横向小路的面积是32xm ,纵向小路的面积是2×20xm ,两者重叠部分的面积是2x m 。
由于花坛的总面积是570m ,则
32×20-(32x+2×20x)+2x =570。
整理,得
x -36x+35=0。
32
20
x
横向小路的面积是32xm ,纵向小路的面积是2×20xm ,两者重叠部分的面积是2x m 。
32×20-(32x+2×20x)+2x =570。
32
20
x
整理得: x -36x+35=0
32
20
(20-x)/2
(32-2x)/3
32-2x 20-x
3 2
=570
6×
整理得:x -36x+35=0
(20-x)(32-2x)=570
32-2x
20-x
32
20
整理得:x -36x+35=0
③都是整式方程
①只含一个未知数
②未知数的最高次数是2
共同特点:
x +2x-1=0
x -36x+35=0
这两个方程有什么共同点?
回忆并说出一元一次方程的概念。
不忘老朋友
只含有一个未知数,且未知数的最高次数是1的整式方程,叫一元一次方程。
标准形式是 a x+ b =0(a,b为常数,且a≠0)。
③都是整式方程
①只含一个未知数
②未知数的最高次数是2
共同特点:
x +2x-1=0
x -36x+35=0
这两个方程有什么共同点?
一元二次方程
一元二次方程的概念
只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程叫做一元二次方程。
结识新朋友
下列方程中哪些是一元二次方程?
是分式
是二次根式
刷题中……
一般形式(标准形式):
ax2+ bx+ c= 0 (a,b,c为常数,a≠0)
其中ax2 bx c
a b
二次项
一次项
常数项
二次项系数
一次项系数
“=”的右边必须整理成0.
ax2+bx =0 (a≠0,b≠0)
完全的一元二次方程:
ax2+bx+c =0 (a≠0, b≠0, c≠0)
不完全的一 元二次方程:
ax2+c =0 (a≠0,c≠0)
ax2=0 (a≠0)
归纳:
一元二次方程的一般形式: ax2+bx+c=0 (a≠0)
3.方程(m+1) x |4m|-2 + 3mx-1=0是关于x的
一元二次方程,则m =
2.下列方程中,无论a为何值,总是关于x的一元二次方程的是( )
A.(2x-1)(x2+3)=2x2 - a B.ax2 + 2x +4=0
C.ax2 + x = x2-1 D.(a2+1)x2=0
行家看门道
1.关于x的方程(k2-1)x2 + 2 (k-1) x + 2=0,
当k 时,是一元二次方程;
当k 时,是一元一次方程。
例1 把方程3x(x-1)=2(x-2)-4化成一般形式,并写出它的二次项系数、一次项系数及常数项。
解: 去括号,得
3x -3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x -5x+8=0.
它的二次项系数是3,一次项系数是-5,
常数项是8。
例题解析
※什么叫方程的根?
※能够使方程左右两边相等的未知数的值,
叫方程的根。
登高望远
例2 已知x=0是关于x的一元二次方程,(m-1)x2 + x+ m2-1=0的一个根,求m的值,并判断x =3是不是方程的根。
已知x=0是关于x的一元二次方程
(m-1)x2 +x +m2-1=0的一个根,求m的值,
并判断x=3是不是方程的根。
这个方程还有没有其它的根?如何去求?
谢 谢
